I/ Cercle trigonométrique et radian
Définition : 1.Cercle trigonométrique
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
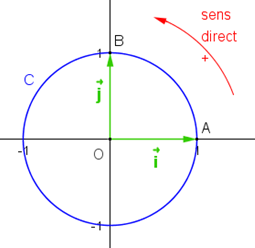
\(\color{red}{\text{Dans un repère orthonormé (O ; I ; J), on appelle cercle trigonométrique le cercle orienté : }}\)
\(\color{red}{\text{C(O, 1) de centre O et de rayon 1.}}\)
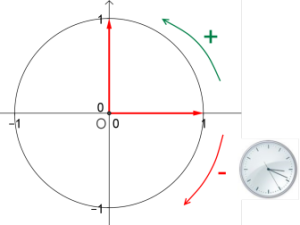
\(\color{red}{\text{Sur ce cercle, on définit une origine I et deux sens :}}\)
\(\color{red}{\text{• Le sens direct ou sens positif est le sens inverse des aiguilles d'une montre ;}}\)
\(\color{red}{\text{• Le sens indirect ou sens négatif est le sens des aiguilles d'une montre.}}\)
Définition : 2. Radians
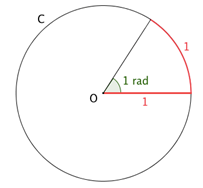
\(\color{red}{\text{On appelle radian, noté rad, la mesure de l'angle au centre }}\)
\(\color{red}{\text{qui intercepte un arc de longueur 1 du cercle de rayon 1.}}\)
Un angle de 360° mesure \(2\pi\) radians.

Complément :
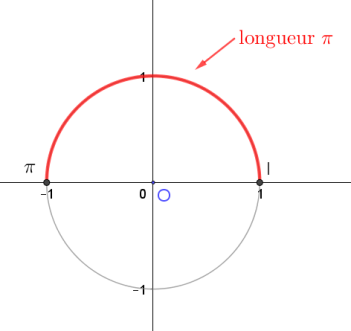
La longueur du cercle trigonométrique est égale à \(2\pi\)
En effet, son rayon est 1 donc P = 2\(\pi\)R = 2\(\pi\) x 1 = 2\(\pi\).
Donc la longueur du cercle trigonométrique est 2π.
Fondamental :
Par proportionnalité, on obtient les correspondances suivantes :
Mesures en degrés | 360° | 180° | 90° | 60° | 45° | 30° | 1° | |
|---|---|---|---|---|---|---|---|---|
Mesures en radians | 1 | \(2\pi\) |
Fondamental :
Mesures en degrés | \(\frac{360}{2\pi}\) | 360° | 180° | 90° | 60° | 45° | 30° | 1° |
|---|---|---|---|---|---|---|---|---|
Mesures en radians | 1 | \(2\pi\) | \(\pi\) | \(\frac{\pi}{2}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{180}\) |
Si on enroule un fil de longueur π autour du cercle en partant du point de coordonnées I(1;0),
l'extrémité atteindra le point de coordonnées (−1;0).