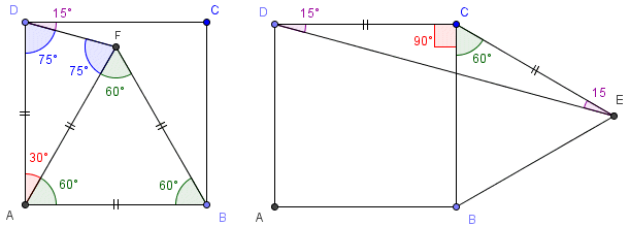
Exercice : Carré - Triangle Equilatéraux
On considère le carré ABCD.
Soit le point E extérieur au carré ABCD tel que le triangle BCE soit équilatéral.
Soit le point intérieur au carré ABCD tel que le triangle ABF soit équilatéral.
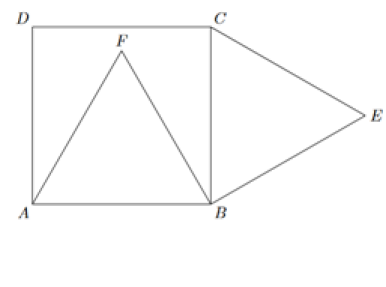
Question
\(\color{magenta}{\text{1ère démonstration}}\)
1. Quelle conjecture peut on faire sur les points D, F et E ?
Solution
Les points D, F et E sont alignés.
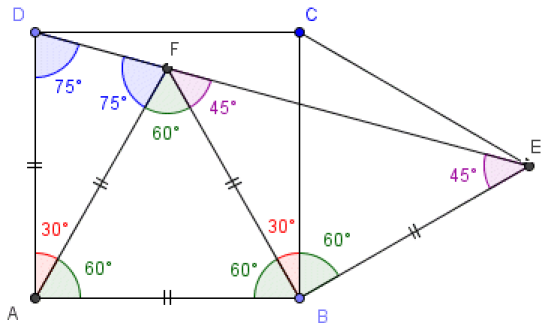
2.a. Donner la mesure des deux angles orientés suivants :
Question
\((\vec{AF} ;\vec{AD})\);
Solution
Le triangle ABE est équilatéral, donc ses trois angles \(\widehat{BAE}\),\(\widehat{AEB}\) et \(\widehat{ABE}\)sont égaux à 60°.
b. Les angles du carré ABCD sont égaux à 90° (angles droits), on en déduit, en utilisant le résultat a, que les angles \(\widehat{DAE}\)et \(\widehat{CBE}\) sont égaux à 30°.
\((\vec{AB} ;\vec{AF})=\frac{\pi}{3}\)
\((\vec{AB} ;\vec{AD})=(\vec{AB} ;\vec{AF})+(\vec{AF} ;\vec{AD})=\frac{\pi}{2}\)
\(\iff (\vec{AF} ;\vec{AD})=\frac{\pi}{2}-(\vec{AB} ;\vec{AF})\)
\(\iff (\vec{AF} ;\vec{AD})=\frac{\pi}{2}-\frac{\pi}{3}\)
\(\iff (\vec{AF} ;\vec{AD})=\frac{3\pi}{6}-\frac{2\pi}{6}\)
\(\iff (\vec{AF} ;\vec{AD})=\frac{\pi}{6}\)
Question
\((\vec{DA} ;\vec{DF})\);
Solution
On a AD=AF donc le triangle ADF est isocèle en A.
Donc ses angles de base \(\widehat{ADE}\) et \(\widehat{DEA}\) sont égaux.
La somme des angles dans un triangle est égale à 180°,
donc \(\widehat{ADE}\)=\(\widehat{DEA}\)=\(\frac{180-30}{2}\)=75°.
\((\vec{DA} ;\vec{DF})+(\vec{FD} ;\vec{FA})+(\vec{AF} ;\vec{AD})=\pi\)
\(\iff (\vec{DA} ;\vec{DF})+(\vec{DA} ;\vec{DF})+(\vec{AF} ;\vec{AD})=\pi\)
\(\iff 2(\vec{DA} ;\vec{DF})+(\vec{AF} ;\vec{AD})=\pi\)
\(\iff 2(\vec{DA} ;\vec{DF})=\pi-(\vec{AF} ;\vec{AD})\)
\(\iff 2(\vec{DA} ;\vec{DF})=\pi-\frac{\pi}{6}\)
\(\iff 2(\vec{DA} ;\vec{DF})=\frac{6\pi}{6}-\frac{\pi}{6}\)
\(\iff 2(\vec{DA} ;\vec{DF})=\frac{5\pi}{6}\)
\(\iff (\vec{DA} ;\vec{DF})=\frac{5\pi}{12}\)

Question
b. En déduire la mesure de l'angle orienté \((\vec{DF} ;\vec{DC})\)
Solution
\((\vec{DA} ;\vec{DC})=(\vec{DA} ;\vec{DF})+(\vec{DF} ;\vec{DC})=\frac{\pi}{2}\)
\(\iff \frac{5\pi}{12}+(\vec{DF} ;\vec{DC})=\frac{\pi}{2}\)
\(\iff (\vec{DF} ;\vec{DC})=\frac{\pi}{2}-\frac{5\pi}{12}\)
\(\iff (\vec{DF} ;\vec{DC})=\frac{6\pi}{12}-\frac{5\pi}{12}\)
\(\iff (\vec{DF} ;\vec{DC})=\frac{\pi}{12}\)
Question
c. Quelle est la nature du triangle CDE ?En déduire la mesure de l'angle orienté \((\vec{DE} ;\vec{DC})\)
Solution
\((\vec{CD} ;\vec{CE})=(\vec{CD} ;\vec{CB})+(\vec{CB} ;\vec{CE})\)
\(\iff (\vec{CD} ;\vec{CE})=\frac{\pi}{2}+\frac{\pi}{3}=\frac{3\pi}{6}+\frac{2\pi}{6}=\frac{5\pi}{6}\)
\(\iff (\vec{CD} ;\vec{CE})+(\vec{DE} ;\vec{DC})+(\vec{EC} ;\vec{ED})=\pi\)
\(\iff \frac{5\pi}{6}+2(\vec{DE} ;\vec{DC})=\pi\)
\(\iff 2(\vec{DE} ;\vec{DC})=\pi-\frac{5\pi}{6}\)
\(\iff 2(\vec{DE} ;\vec{DC})=\frac{6\pi}{6}-\frac{5\pi}{6}\)
\(\iff 2(\vec{DE} ;\vec{DC})=\frac{\pi}{6}\)
\(\iff (\vec{DE} ;\vec{DC})=\frac{\pi}{12}\)
Question
3.En déduire la conjecture.
Solution
\(\begin{cases}(\vec{DF} ;\vec{DC})=\frac{\pi}{12}\\ (\vec{DE} ;\vec{DC})=\frac{\pi}{12} \end{cases}\)
donc D,E et F sont alignés.
\(\color{magenta}{\text{2ème démonstration}}\)
On appelle G le point d'intersection des droites (AF) et (CD).
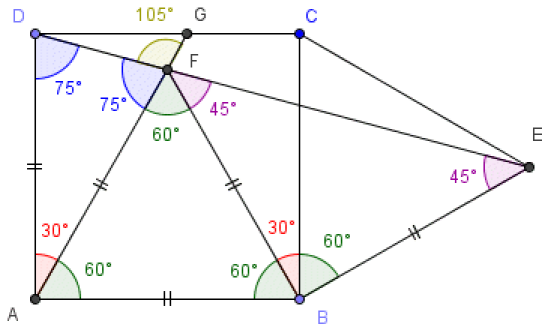
Question
1.a.Quelle est la mesure de l'angle \(\widehat{AEF}\)?
Solution
En reprenant certains résultats de la méthode 1, on a :
\(\widehat{AFB}\)=60° et \(\widehat{BFE}\)=45°
\(\widehat{AFE}\)=60+45=105°
Question
b. Quelle est la mesure de l'angle \(\widehat{DFG}\)?
Solution
On a \(\widehat{AFD}\)=75°.
Les points A, E et G sont alignés donc \(\widehat{AFG}\)=180° donc \(\widehat{DFG}\)=180-75=105°.
Question
2.En déduire la conjecture.
Solution
\(\)On a montré que \(\widehat{AEF}=\widehat{DEG}=105°\).
De plus, ces deux angles ont chacun un côté porté par une même droite ( les côtés [EG) et [EA) )
donc ce sont des angles opposés par le sommet, donc les points D, E et F sont alignés.
\(\color{magenta}{\text{3ème démonstration}}\)
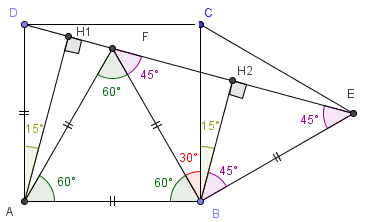
Dans le triangle ADE, on appelle \(H_1\) le pied de la hauteur issue de A.
Dans le triangle BEF, on appelle \(H_2\) le pied de la hauteur issue de B.
a. Dans la méthode 1, on a montré que le triangle DAE est isocèle est A et que l'angle \(\widehat{DAE}\)=30°.
Dans un triangle isocèle, la hauteur issue du sommet principal est confondue avec la bissectrice issue du même sommet, on en déduit que \(\widehat{DAH_1}\)=15°.
b. Dans la méthode 1, on a montré que le triangle BEF est rectangle isocèle est B et que l'angle \(\widehat{BFE}=45°\).
Dans un triangle isocèle, la hauteur issue du sommet principal est confondue avec la bissectrice issue du même sommet, on en déduit que \(\widehat{FBH_2}=45°\).
c. Le triangle BCF est équilatéral donc \(\widehat{FBC}=60°\).
En utilisant le résultat b, on a : \(\widehat{CBH_2}=60-45=15\).
Conclusion : On a montré que \(\widehat{DAH_1}=\widehat{CBH_2}\).
Les droites (AD) et (BC) étant parallèles, on en déduit que les droites (AH1) et (BH2) sont parallèles.
Les droites (AH1) et (BH2) sont respectivement perpendiculaires aux droites (DE) et (EF).
Les droites (DE) et (EF) sont donc parallèles entre elles, et comme elles ont le point E en commun, elles sont confondues, donc les points D, E et F sont alignés.
Remarque : on peut adapter les méthodes 1 à 4 au niveau 1ère avec des angles orientés de vecteurs \(( \vec{ED},\vec{EF})\) plutôt qu'avec des angles géométriques, ainsi que de travailler en radians plutôt qu'en degrés.
\(\color{magenta}{\text{4ème démonstration}}\)
On appelle :
H le projeté orthogonal de E sur (AB)
G le projeté orthogonal de F sur (BC)
M le projeté orthogonal de E sur (CD)
N le projeté orthogonal de F sur (CD)
K le projeté orthogonal de F sur (EH)
On considère que le carrée ABCD a un côté de longueur unité AB=1.
Question
a. calcul de la longueur HE
Solution
Le triangle AHE est rectangle en H, donc d'après Pythagore :
De la même manière, on a \(GF=\frac{\sqrt{3}}{2}\)
b. calcul de la longueur ME
ME=MH-HE
ME=1-\(\frac{\sqrt{3}}{2}\)
ME=\(\frac{2-\sqrt{3}}{2}\)
c. calcul de la longueur EK
EK=EH-KH
\(EK=\frac{\sqrt{3}}{2}-\frac{1}{2}\)
\(EK=\frac{\sqrt{3}-1}{2}\)
d. calcul de la longueur KF
KF=KG+GF
KF=\(\frac{1}{2}\)+\(\frac{\sqrt{3}}{2}\)
KF=\(\frac{1+\sqrt{3}}{2}\)
e. calcul de la longueur DN
DN=DC+CN
DN=1+\(\frac{\sqrt{3}}{2}\)
DN=\(\frac{2+\sqrt{3}}{2}\)
f. calcul de la longueur DE
Le triangle DME est rectangle en M, donc d'après le théorème de Pythagore.
g. calcul de la longueur EF
Le triangle EFK est rectangle en K, donc d'après le théorème de Pythagore.
h. calcul de la longueur DF
Le triangle DFN est rectangle en N, donc d'après le théorème de Pythagore.
i. démontrons que DF=DE+EF
\(\textbf{Conclusion :}\) On a démontré que DF = DE + EF donc les points D, E et F sont alignés.