Exercices
Exemple :
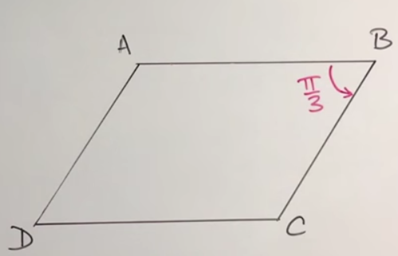
ABCD est un parallélogramme.
Déterminer la mesure des angles :
1. \((\vec{AD} ;\vec{AB})\)
2. \((\vec{CB} ;\vec{DC})\)
Complément :
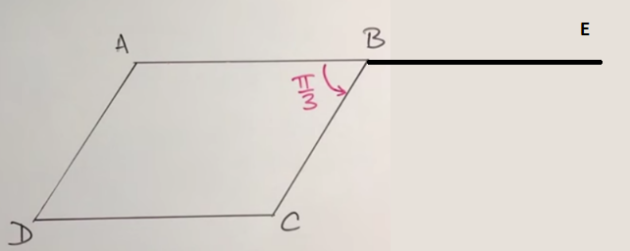
1. \((\vec{BA} ;\vec{BC})+(\vec{BC} ;\vec{BE})=(\vec{BA} ;\vec{BE})=\pi\)
\(\begin{cases}\vec{BC}=\vec{AD}\\\vec{BE}=\vec{AB}\end{cases}\)
donc
\((\vec{BA} ;\vec{BC})+(\vec{BC} ;\vec{BE})=\frac{\pi}{3}+(\vec{AD} ;\vec{AB})\)
donc
\(\frac{\pi}{3}+(\vec{AD} ;\vec{AB})=\pi\)
\(\iff (\vec{AD} ;\vec{AB})=\pi-\frac{\pi}{3}\)
\(\iff (\vec{AD} ;\vec{AB})=\frac{3\pi}{3}-\frac{\pi}{3}\)
\(\iff (\vec{AD} ;\vec{AB})=\frac{2\pi}{3}\)
2.
\((\vec{CB} ;\vec{DC})=(\vec{DA} ;\vec{DC})=(-\vec{BC} ;-\vec{BA})=(\vec{BC} ;\vec{BA})=-\frac{\pi}{3}\)
Exemple :
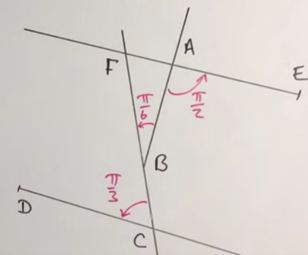
Déterminer la mesure de l'angle orienté \((\vec{CD} ;\vec{AE})\)
Que peut on en déduire pour les droites (CD) et (AE)
Complément :
\((\vec{CD} ;\vec{AE})=(\vec{CD} ;\vec{CF})+(\vec{CF} ;\vec{BA})+(\vec{BA} ;\vec{AE})\)
\(\iff (\vec{CD} ;\vec{AE})=\frac{-\pi}{3}+\frac{-\pi}{6}+\frac{-\pi}{2}\)
\(\iff (\vec{CD} ;\vec{AE})=\frac{-2\pi}{6}+\frac{-\pi}{6}+\frac{-3\pi}{6}\)
\(\iff (\vec{CD} ;\vec{AE})=\frac{-6\pi}{6}=-\pi\)
Les droites (CD) et (AE) sont donc parallèles.