VI/ Equations trigonométriques
Exemple :
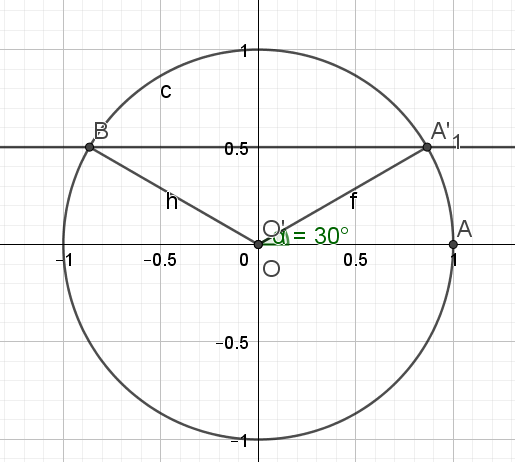
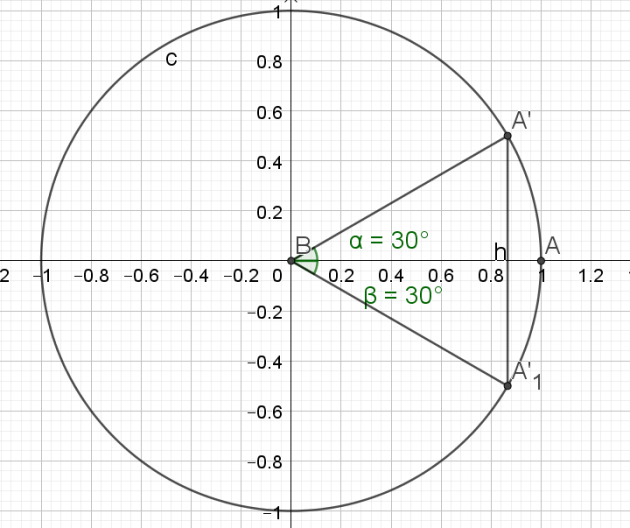
\(cos x= cos \frac{\pi}{6}\)
Complément :
Méthode : Equation cos x = cos a
\(\color{red}{\text{Soit } a \text{ un nombre réel.}}\)
\(\color{red}{cos x = cos a \text{ a pour solutions } S=\{ a+2k\pi;- a+2k\pi \} k∈\mathbb{Z}}\)
Fondamental :
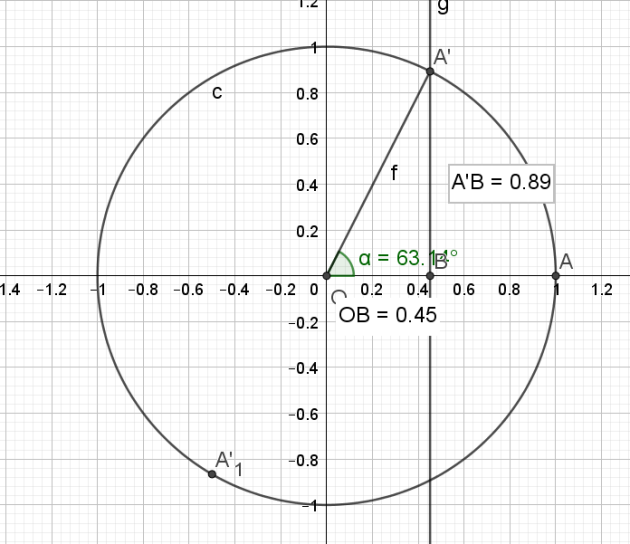
\(sin x=-0,5\)
Complément :
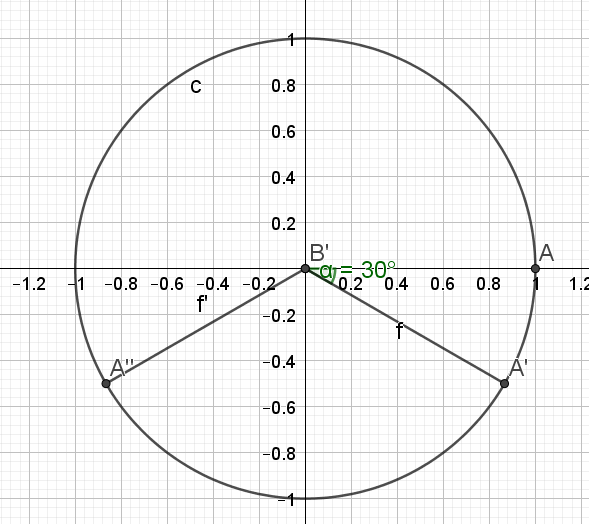
\(sin x=-0,5\)
\(\iff sin x=sin(-\frac{\pi}{6})\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi \\ x=\pi-(-\frac{\pi}{6})+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi \\ x=\pi+\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi \\ x=\frac{6\pi}{6}+\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi \\ x=\frac{7\pi}{6}+2k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Fondamental :
\(\color{red}{\text{Soit } a \text{ un nombre réel.}}\)
\(\color{red}{ sin x = sin a \text{ a pour solutions } S=\{a+2k\pi;\pi- a+2k\pi\}} \) \(\color{red}{k∈\mathbb{Z}}\)
Exemple :
Résoudre dans \(\mathbb{R}\), l'équation :
\(sin(3x)=1\)
Complément :
\(sin(3x)=sin(\frac{\pi}{2})\)
\(\iff \begin{cases}3x=\frac{\pi}{2}+2k\pi\\3x=\pi-\frac{\pi}{2}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+\frac{2k\pi}{3}\\3x=\frac{\pi}{2}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{6}+\frac{2k\pi}{3}\\x=\frac{\pi}{6}+\frac{2k\pi}{3}\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff x=\frac{\pi}{6}+\frac{2k\pi}{3}\) \(k \in \mathbb{Z}\)
Les mesures principales correspondantes sont :
Pour \(k=0\): \(\frac{\pi}{6}\)
Pour \(k=1\):\(\frac{\pi}{6}+\frac{2\pi}{3}=\frac{\pi}{6}+\frac{4\pi}{6}=\frac{5\pi}{6}\)
Pour \(k=2\):
\(\frac{\pi}{6}+\frac{4\pi}{3}=\frac{\pi}{6}+\frac{8\pi}{6}=\frac{9\pi}{6}-2\pi\)
\(=\frac{9\pi}{6}-\frac{12\pi}{6}=\frac{-3\pi}{6}=\frac{-\pi}{2}\)
Pour \(k=3\):\(\frac{\pi}{6}+\frac{6\pi}{3}=\frac{\pi}{6}+2\pi=\frac{\pi}{6}\)
On retrouve la valeur pour \(k=0\), inutile de prendre des valeurs de \(k\) supérieures car on ajoute \(\frac{2\pi}{3}\)
entre deux angles successifs.
Pour \(k=-1\): \(\frac{\pi}{6}+\frac{-2\pi}{3}=\frac{\pi}{6}-\frac{4\pi}{6}=\frac{-3\pi}{6}=-\frac{\pi}{2}\)
On retrouve la valeur pour \(k=2\), inutile de prendre des valeurs de \(k\) inférieures car on soustrait \(\frac{2\pi}{3}\)
entre deux angles successifs.
Exemple :
On donne la valeur exacte ci-dessous :
\(cos(\frac{\pi}{8})=\frac{\sqrt{2+\sqrt{2}}}{2}\)
1.En utilisant la formule \((cos x)^2+(sin x)^2=1\)
déterminer la valeur exacte de \(sin(\frac{\pi}{8})\)
2.En déduire la valeur exacte de \(cos(\frac{5\pi}{8})\), en justifiant votre démarche.
3.Etablir l'égalité : \(tan(\frac{\pi}{8})=\sqrt{3-2\sqrt{2}}\)
Complément :
\(cos(\frac{\pi}{8})=\frac{\sqrt{2+\sqrt{2}}}{2}\)
\((cos (\frac{\pi}{8}))^2+(sin (\frac{\pi}{8}))^2=1\)
\(\iff (\frac{\sqrt{2+\sqrt{2}}}{2})^2+(sin (\frac{\pi}{8}))^2=1\)
\(\iff \frac{2+\sqrt{2}}{4}+(sin (\frac{\pi}{8}))^2=1\)
\(\iff (sin (\frac{\pi}{8}))^2=1-\frac{2+\sqrt{2}}{4}\)
\(\iff (sin (\frac{\pi}{8}))^2=\frac{4}{4}-\frac{2+\sqrt{2}}{4}\)
\(\iff (sin (\frac{\pi}{8}))^2=\frac{4-(2+\sqrt{2})}{4}\)
\(\iff (sin (\frac{\pi}{8}))^2=\frac{4-2-\sqrt{2}}{4}\)
\(\iff (sin (\frac{\pi}{8}))^2=\frac{2-\sqrt{2})}{4}\)
\(\iff sin (\frac{\pi}{8})=\sqrt{\frac{2-\sqrt{2}}{4}}\) ou \(sin (\frac{\pi}{8})=-\sqrt{\frac{2-\sqrt{2}}{4}}\)
\(\iff sin (\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}\) ou \(sin (\frac{\pi}{8})=\frac{-\sqrt{2-\sqrt{2}}}{2}\)
or \(\frac{\pi}{8}\in[0 ; \frac{\pi}{2}]\) donc \(sin(\frac{\pi}{8})\ge 0\)
donc \(sin (\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}\)
2. \(cos(\frac{5\pi}{8})=cos(\frac{4\pi}{8}+\frac{\pi}{8})=cos(\frac{\pi}{2}+\frac{\pi}{8})=-sin(\frac{\pi}{8})\)
\(\iff cos(\frac{5\pi}{8})=-\frac{\sqrt{2-\sqrt{2}}}{2}\)
3.\(tan(\frac{\pi}{8})=\frac{sin(\frac{\pi}{8})}{cos(\frac{\pi}{8})}\)
\(\iff tan(\frac{\pi}{8})=\frac{\frac{\sqrt{2-\sqrt{2}}}{2}}{\frac{\sqrt{2+\sqrt{2}}}{2}}\)
3\(\iff tan(\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2} \times \frac{2}{\sqrt{2+\sqrt{2}}}\)
\(\iff tan(\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}\)
\(\iff tan(\frac{\pi}{8})=\frac{(\sqrt{2-\sqrt{2}})(\sqrt{2-\sqrt{2}})}{(\sqrt{2+\sqrt{2}})(\sqrt{2-\sqrt{2}})}\)
\(\iff tan(\frac{\pi}{8})=\frac{2-\sqrt{2}}{\sqrt{2^2-\sqrt{2}^2}}\)
\(\iff tan(\frac{\pi}{8})=\frac{2-\sqrt{2}}{\sqrt{4-2}}\)
\(\iff tan(\frac{\pi}{8})=\frac{2-\sqrt{2}}{\sqrt{2}}\)
\(\iff tan(\frac{\pi}{8})=\frac{2}{\sqrt{2}}-\frac{\sqrt{2}}{\sqrt{2}}\)
\(\iff tan(\frac{\pi}{8})=\sqrt{2}-1\)
\((\sqrt{3-2\sqrt{2}})^2=3-2\sqrt{2}\)
\((\sqrt{2}-1)^2=3-2\sqrt{2}\)
donc \(\sqrt{3-2\sqrt{2}}=\sqrt{(\sqrt{2}-1)^2}=\sqrt{2}-1\)
Finalement \(tan(\frac{\pi}{8})=\sqrt{3-2\sqrt{2}}\)
Exemple :
Résoudre dans \(\mathbb{R}\) les équations suivantes :
\(2cos^2 x+2\sqrt{2} cos x+1=0\)
Complément :
\(2cos^2 x+2\sqrt{2} cos x+1=0\)
Posons \(X=cosx\)
donc \(X \in [0 ;1]\)
\(2X^2+2\sqrt{2}X+1=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(2\sqrt{2})^2-4\times 2 \times 1\)
\(\iff \Delta= 4\times 2-4\times 2\)
\(\iff \Delta=8-8\)
\(\iff \Delta=0\)
donc l'équation n'admet qu'une seule solution :
\(X_0=\frac{-b}{2a}=\frac{-2\sqrt{2}}{2\times 2}\)
\(\iff X_0=\frac{-2\sqrt{2}}{4}\)
\(\iff X_0=\frac{-\sqrt{2}}{2}\)
\(\iff cos x=\frac{-\sqrt{2}}{2}\)
\(\iff x= \frac{\pi}{4}+2k\pi\) ou \(x= -\frac{\pi}{4}+2k\pi\) \(k\in \mathbb{Z}\)
Exemple :
\(2 sin^2 x+5sin x-3=0\)
Complément :
\(2 sin^2 x+5sin x-3=0\)
Posons \(X=sinx\)
donc \(X \in [0 ;1]\)
\(2X^2+5X-3=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=5^2-4\times 2 \times (-3)\)
\(\iff \Delta=25+24\)
\(\iff \Delta=49\)
\(\iff \Delta=49\)
donc l'équation admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-5-\sqrt{49}}{2\times 2}\\X_2=\frac{-5+\sqrt{49}}{2\times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-5-7}{4}\\X_2=\frac{-5+7}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-12}{4}\\X_2=\frac{2}{4}\end{cases}\)
\(\iff \begin{cases}X_1=-3\\X_2=\frac{1}{2}\end{cases}\)
or \(X \in [0 ;1]\) donc \(X_1=-3\) est impossible
\(X_2=\frac{1}{2}\)
\(\iff sin x =\frac{1}{2}\)
\(\iff x= \frac{\pi}{6}+2k\pi\) ou \(x= \pi-\frac{\pi}{6}+2k\pi\) \(k \in\mathbb{Z}\)