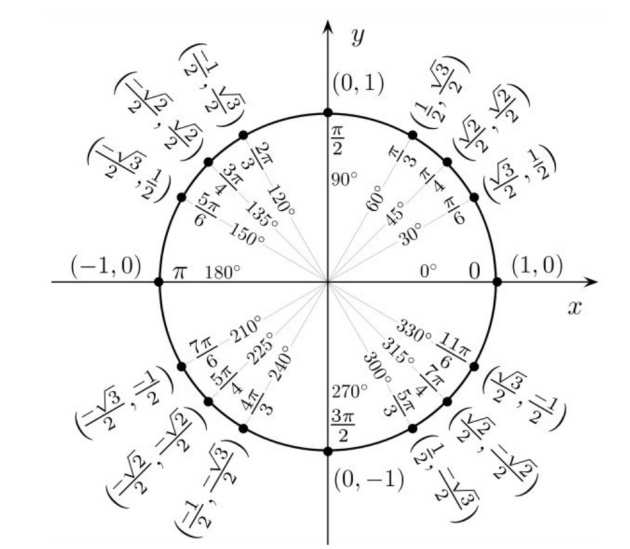
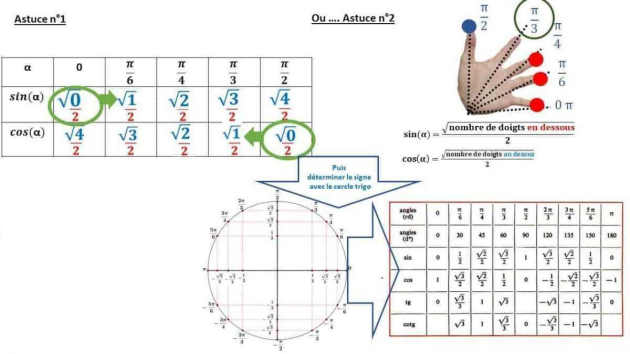
V/ Cosinus et sinus d'un angle
Définition :
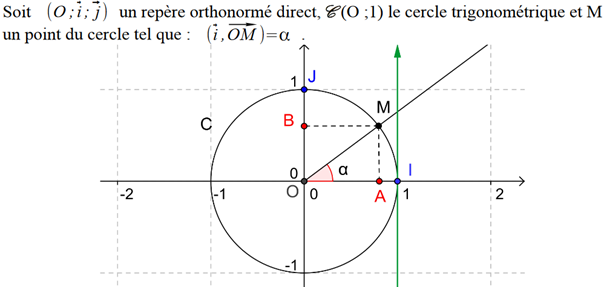
\(\color{red}{\text{Le cosinus du nombre réel } x \text{ est l'abscisse de M et on note } cos \; x.}\)
\(\color{red}{\text{Le sinus du nombre réel } x \text{ est l'ordonnée de M et on note } sin \; x.}\)
Complément : a. Calcul du cosinus et du sinus de π/4
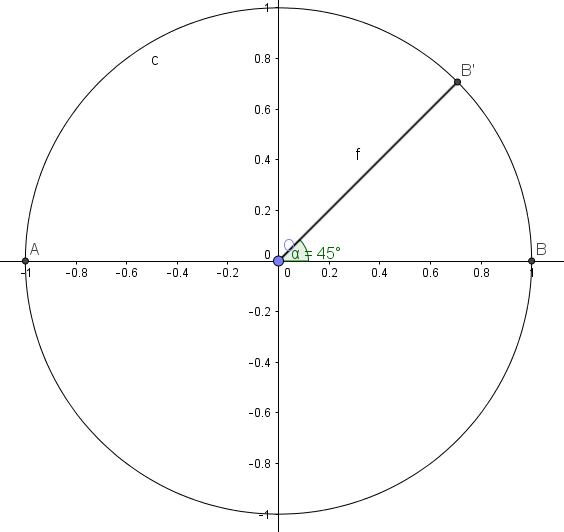
Complément :
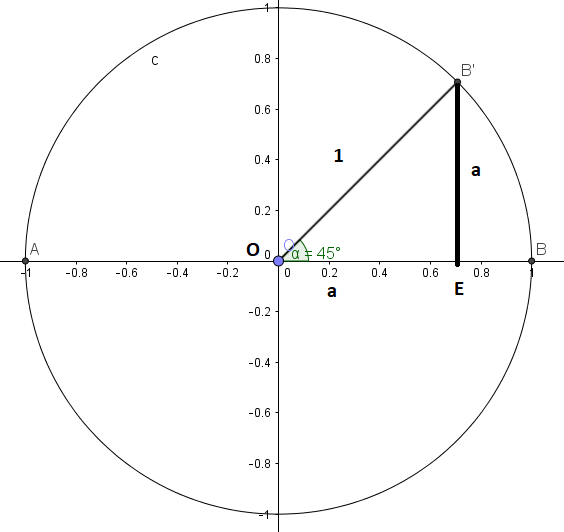
\(\widehat{OEB'}+\widehat{EB'O}+\widehat{B'OE}=\pi\)
\(\iff \frac{\pi}{2}+\widehat{EB'O}+\frac{\pi}{4}=\pi\)
\(\iff \widehat{EB'O}=\pi-\frac{\pi}{2}-\frac{\pi}{4}\)
\(\iff \widehat{EB'O}=\frac{\pi}{4}\)
Le triangle OB'E est donc un triangle équilatéral car il a deux angles égaux(\(\frac{\pi}{4}\)).
\(OE^2+EB'^2=OB'^2\)
\(\iff a^2+a^2=1^2\)
\(\iff 2a^2=1\)
\(\iff a^2=\frac{1}{2}\)
\(\iff a=\sqrt{\frac{1}{2}}\)
\(\iff a=\frac{\sqrt{1}}{\sqrt{2}}\)
\(\iff a=\frac{1}{\sqrt{2}}\)
\(\iff a=\frac{\sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)
\(\iff a=\frac{\sqrt{2}}{2}\)
\(cos(\frac{\pi}{4})=\frac{ \text{côté adjacent}}{\text{hypoténuse}}\)
\(\iff cos(\frac{\pi}{4})=\frac{OE}{OB'}\)
\(\iff cos(\frac{\pi}{4})=\frac{a}{1}\)
\(\iff cos(\frac{\pi}{4})=a\)
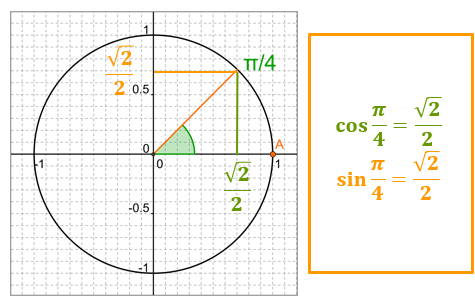
\(\color{red}{cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2}}\)
\(sin(\frac{\pi}{4})=\frac{\text{côté opposé}}{\text{hypoténuse}}\)
\(\iff sin(\frac{\pi}{4})=\frac{EB'}{OB'}\)
\(\iff sin(\frac{\pi}{4})=\frac{a}{1}\)
\(\iff sin(\frac{\pi}{4})=a\)
\(\color{red}{sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}}\)
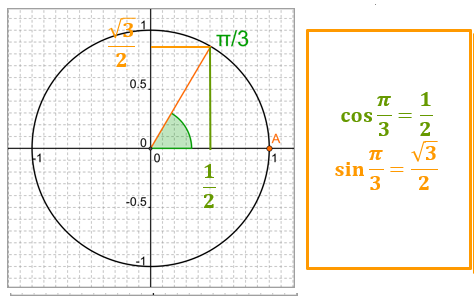
Exemple : b. Calcul du cosinus et du sinus de π/3
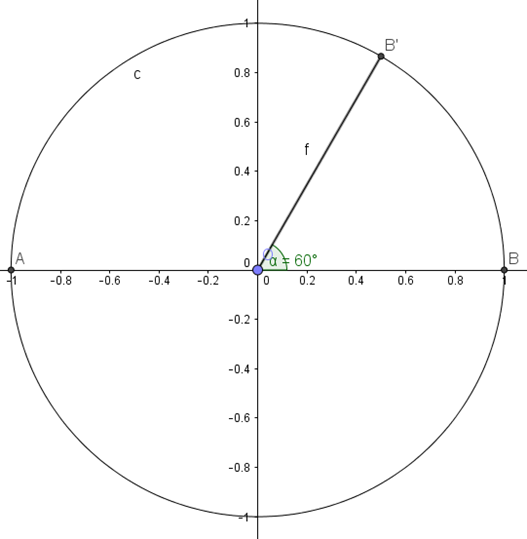
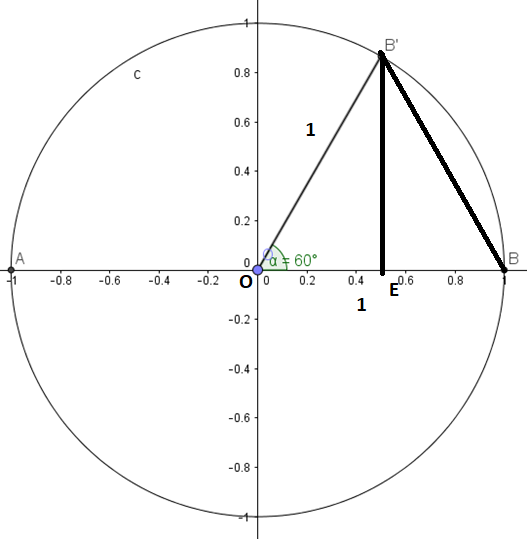
Le triangle OBB' est équilatéral car il a deux côtés de même longueur 1
donc \(\widehat{OB'B}=\widehat{OBB'}\)
\(\widehat{OB'B}+\widehat{OBB'}+\widehat{B'OB}=\pi\)
\(2\widehat{OB'B}+\frac{\pi}{3}=\pi\)
\(2\widehat{OB'B}=\pi-\frac{\pi}{3}\)
\(2\widehat{OB'B}=\frac{2\pi}{3}\)
\(\widehat{OB'B}=\frac{\pi}{3}\)
Les trois angles du triangle sont donc égaux,
on déduit que le triangle OBB' est un triangle équilatéral.
La hauteur (BE') est donc aussi une médiatrice du côté [OB']
en effet B est équidistant des points O et B' et (BE') est perpendiculaire à [OB']
donc
\(OE=EB=\frac{1}{2}\)
\(OE^2+EB'^2=OB'^2\)
\(\iff (\frac{1}{2})^2+EB'^2=1^2\)
\(\iff \frac{1}{4}+EB'^2=1\)
\(\iff EB'^2=1-\frac{1}{4}\)
\(\iff EB'^2=\frac{4}{4}-\frac{1}{4}\)
\(\iff EB'^2=\frac{3}{4}\)
\(\iff EB'=\sqrt{\frac{3}{4}}\)
\(\iff EB'=\frac{\sqrt{3}}{2}\)
\(cos(\frac{\pi}{3})=\frac{\text{côté adjacent}}{\text{hypoténuse}}\)
\(\iff cos(\frac{\pi}{3})=\frac{OE}{OB'}\)
\(\iff cos(\frac{\pi}{3})=\frac{\frac{1}{2}}{1}\)
\(\iff cos(\frac{\pi}{3})=\frac{1}{2}\)
\(\color{red}{cos(\frac{\pi}{3})=\frac{1}{2}}\)
\(sin(\frac{\pi}{3})=\frac{\text{côté opposé}}{\text{hypoténuse}}\)
\(\iff sin(\frac{\pi}{3})=\frac{EB'}{OB'}\)
\(\iff sin(\frac{\pi}{3})=\frac{\frac{\sqrt{3}}{2}}{1}\)
\(\iff sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}\)
\(\color{red}{sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}}\)
Fondamental : Valeurs remarquables des fonctions sinus et cosinus :
\(x\) | 0 | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\pi\) |
|---|---|---|---|---|---|---|
\(cos x\) | ||||||
\(sin x\) |
\(x\) | 0 | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\pi\) |
|---|---|---|---|---|---|---|
\(cos x\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | 0 | -1 |
\(sin x\) | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | 1 | 0 |
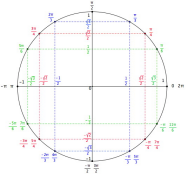
Exemple :
Après avoir placé sur un cercle, les angles dont une mesure est donnée ci-dessous puis trouvez les valeurs des cosinus et des sinus des angles ci-dessous :


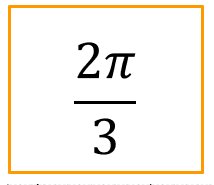
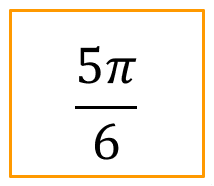
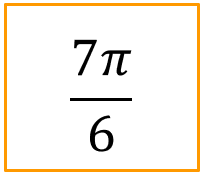
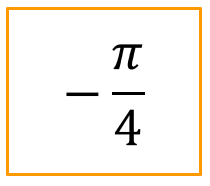
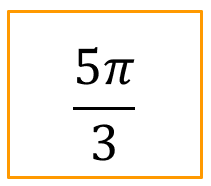
Définition : 2) Propriétés
Pour tout nombre réel \(x\), on a :
1.\(-1 \le cos x\le 1\)
2.\(-1 \le sin x\le 1\)
3. \(cos^2 x + sin^2 x = 1\)
4. \(cos(x+2k\pi)=cos x\) où k entier relatif
5. \(sin(x+2k\pi)=sin x\)où k entier relatif