II/ Mesure principale d'un angle
Méthode :
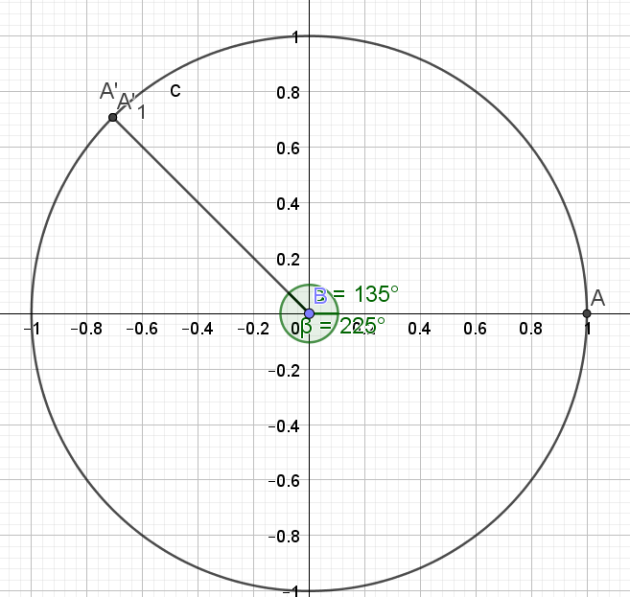
1. Placer sur le cercle trigonométrique les angles de mesure \(\frac{3\pi}{4}\) et \(\frac{-5\pi}{4}\). Qu'observez vous ?
2. Placer sur le cercle l'angle de mesure \(\frac{19\pi}{4}\). Qu'observez vous ?
Complément :
1.Les angles de mesure \(\frac{3\pi}{4}\) et \(\frac{-5\pi}{4}\) correspondent au même point sur le cercle trigonométrique.
En effet :
\(\frac{3\pi}{4}-\frac{-5\pi}{4}=\frac{3\pi}{4}+\frac{5\pi}{4}=\frac{8\pi}{4}=2\pi\)
Les deux angles \(\frac{3\pi}{4}\) et \(\frac{-5\pi}{4}\) sont donc séparés de \(2\pi\) et donc d'un tour :
ils correspondent donc à un même point sur le cercle.
2.Les angles de mesure \(\frac{3\pi}{4}\) et \(\frac{19\pi}{4}\) correspondent au même point sur le cercle trigonométrique.
En effet :
\(\frac{19\pi}{4}-\frac{3\pi}{4}=\frac{16\pi}{4}=4\pi=2 \times 2\pi\)
Les deux angles \(\frac{3\pi}{4}\) et \(\frac{19\pi}{4}\) sont donc séparés de \(2 \times 2\pi\) et donc de deux tours :
ils correspondent donc à un même point sur le cercle.
Définition :
\(\color{red}{\text{La mesure principale d'un angle orienté est la mesure,}}\)
\(\color{red}{\text{ qui parmi toutes les autres, se situe dans l'intervalle} ]-\pi;\pi]. }\)
Exemple :
Déterminer la mesure principale de l'angle \(\frac{27π}{4}\)
Complément :
\(\frac{\frac{27π}{4}}{2\pi}=\frac{27π}{4} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{27π}{4}}{2\pi}=\frac{27π}{8\pi}\)
\(\iff \frac{\frac{27π}{4}}{2\pi}=\frac{27}{8}\)
\(\frac{24}{8} \le \frac{27}{8} \le \frac{32}{8}\)
\(3 \le \frac{27}{8} \le 4\)
donc \(\frac{27π}{4}\) est compris entre 3 et 4 tours.
\(\frac{27π}{4}-3\times 2\pi=\frac{27π}{4}-6\pi\)
\(\iff \frac{27π}{4}-3\times 2\pi=\frac{27π}{4}-\frac{24π}{4}\)
\(\iff \frac{27π}{4}-3\times 2\pi=\frac{3π}{4}\in]-\pi ;\pi]\)
\(\frac{27π}{4}-4\times 2\pi=\frac{27π}{4}-8\pi\)
\(\iff \frac{27π}{4}-4\times 2\pi=\frac{27π}{4}-\frac{32π}{4}=\frac{-5π}{4}\notin]-\pi ;\pi]\)
La mesure principale de \(\frac{27π}{4}\) est donc \(\frac{3π}{4}\)
Exemple :
Déterminer la mesure principale de l'angle \(\frac{-17π}{3}\)
Complément :
\(\frac{\frac{-17π}{3}}{2\pi}=\frac{-17π}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-17π}{3}}{2\pi}=\frac{-17π}{6\pi}\)
\(\iff \frac{\frac{-17π}{3}}{2\pi}=\frac{-17}{6}\)
\(\frac{-18}{6} \le \frac{-17}{6} \le \frac{-12}{6}\)
\(-3 \le \frac{-17}{6} \le -2\)
donc \(\frac{-17π}{3}\) est compris entre -3 et -2 tours.
\(\frac{-17π}{3}-(-3) \times 2\pi=\frac{-17π}{3}+6\pi\)
\(\iff \frac{-17π}{3}-(-3) \times 2\pi=\frac{-17π}{3}+\frac{18π}{3}\)
\(\iff \frac{-17π}{3}-(-3)\times 2\pi=\frac{π}{3}\in]-\pi ;pi]\)
\(\frac{-17π}{3}-(-2)\times 2\pi=\frac{-17π}{3}+4\pi\)
\(\iff \frac{-17π}{3}-(-2)\times 2\pi=\frac{-17π}{3}+\frac{12π}{4}=\frac{-5π}{3}\notin]-\pi ;\pi]\)
La mesure principale de \(\frac{-17π}{3}\) est donc \(\frac{π}{3}\)
Exemple :
Déterminer la mesure principale de l'angle \(x=\frac{273π}{12}\)
Complément :
\(\frac{\frac{273π}{12}}{2\pi}=\frac{273π}{12} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{273π}{12}}{2\pi}=\frac{273π}{24\pi}\)
\(\iff \frac{\frac{273π}{12}}{2\pi}=\frac{273}{24}\)
\(\frac{264}{24} \le \frac{273}{24} \le \frac{288}{24}\)
\(11 \le \frac{273}{24} \le 12\)
donc \(\frac{273π}{12}\) est compris entre 11 et 12 tours.pi
\(\frac{273π}{12}-11\times 2\pi=\frac{273π}{12}-22\pi\)
\(\iff \frac{273π}{12}-11\times 2\pi=\frac{273π}{12}-\frac{264π}{12}\)
\(\iff \frac{273π}{12}-11\times 2\pi=\frac{9π}{12}=\frac{3π}{4}\in]-\pi ;\pi]\)
\(\frac{273π}{12}-12\times 2\pi=\frac{273π}{12}-24\pi\)
\(\iff \frac{273π}{12}-12\times 2\pi=\frac{273π}{12}-\frac{288π}{12}\)
\(\iff \frac{273π}{12}-11\times 2\pi=\frac{-15π}{12}=\frac{-5π}{4}\notin]-\pi ;\pi]\)
La mesure principale de \(\frac{273π}{12}\) est donc \(\frac{3π}{4}\)
Exemple :
Déterminer la mesure principale de l'angle \(x=\frac{89π}{12}\)
Complément :
\(\frac{\frac{89π}{12}}{2\pi}=\frac{89π}{12} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{89π}{12}}{2\pi}=\frac{89π}{24\pi}\)
\(\iff \frac{\frac{89π}{12}}{2\pi}=\frac{89}{24}\)
\(\frac{72}{24} \le \frac{89}{24} \le \frac{96}{24}\)
\(3 \le \frac{89}{24} \le 4\)
donc \(\frac{89π}{12}\) est compris entre 3 et 4 tours.
\(\frac{89π}{12}-3\times 2\pi=\frac{89π}{12}-6\pi\)
\(\iff \frac{89π}{12}-3\times 2\pi=\frac{89π}{12}-\frac{72π}{12}\)
\(\iff \frac{89π}{12}-3\times 2\pi=\frac{17π}{12}\notin]-\pi ;\pi]\)
\(\frac{89π}{12}-4\times 2\pi=\frac{89π}{12}-8\pi\)
\(\iff \frac{89π}{12}-4\times 2\pi=\frac{89π}{12}-\frac{96π}{12}\)
\(\iff \frac{89π}{12}-4\times 2\pi=\frac{-7π}{12}\in]-\pi ;\pi]\)
La mesure principale de \(\frac{89π}{12}\) est donc \(\frac{-7π}{12}\)
Exemple :
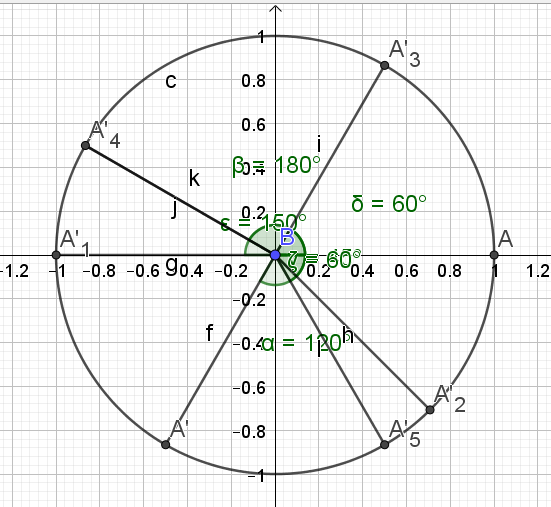
Placer sur le cercle trigonométrique les points correspondants à des mesures des angles de
\(\frac{-\pi}{6}\);\(\frac{3\pi}{4}\);12π;\(\frac{9\pi}{2}\);\(\frac{\pi}{12}\);15π;\(\frac{-5\pi}{6}\);\(\frac{13\pi}{3}\)
Complément :
Déterminons les mesures principales des angles :
\(\frac{-\pi}{6}\in]-\pi ;\pi](A')\)
\(\frac{3\pi}{4}\in]-\pi ;\pi](A'_1)\)
\(12π= 6 \times 2\pi \mapsto 0 \in]-pi ;\pi](A)\)
\(\frac{9\pi}{2}= \frac{8\pi}{2}+\frac{\pi}{2}=4\pi+\frac{\pi}{2}\mapsto \frac{\pi}{2} \in]-\pi ;\pi](A'_2)\)
\(\frac{\pi}{12}\in]-\pi ;pi](A'_3)\)
\(15π=14 \pi +\pi=7 \times 2\pi +\pi\mapsto \pi in]-\pi ;\pi](A'_4)\)
\(\frac{-5\pi}{6} in]-\pi ;\pi](A'_5)\)
\(\frac{13\pi}{3}=\frac{12\pi}{3}+\frac{\pi}{3}=4\pi+\frac{\pi}{3}\)
\(\iff \frac{13\pi}{3}=2 \times 2\pi+\frac{\pi}{3} \mapsto \frac{\pi}{3}(A'_6)\)
Exemple :
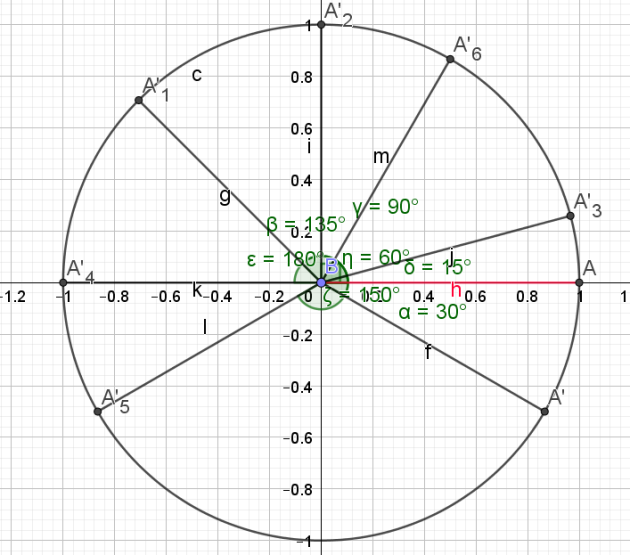
Placer sur le cercle trigonométrique les points correspondants à des mesure des angles de :
\(\frac{4\pi}{3}\); -21π;\(\frac{-9\pi}{4}\);\(\frac{-17\pi}{3}\);\(\frac{17\pi}{6}\);\(\frac{-121\pi}{3}\)
Complément :
Déterminons les mesures principales des angles :
1. \(\frac{\frac{4\pi}{3}}{2\pi}=\frac{4\pi}{3}\times \frac{1}{2\pi}\)
\(\iff \frac{\frac{4\pi}{3}}{2\pi}=\frac{4\pi}{6\pi}\)
\(\iff \frac{\frac{4\pi}{3}}{2\pi}=\frac{4}{6}=\frac{2}{3}\)
\(0 \le \frac{2}{3} \le 1\)
\(\frac{4\pi}{3}-0 \times 2\pi\)
\(=\frac{4\pi}{3}\notin]-\pi ;\pi]\)
\(=\frac{4\pi}{3}-\frac{6\pi}{3}\)
\(=\frac{-2\pi}{3}\in]-\pi ;\pi](A')\)
2.
\(\frac{-21π}{2\pi}=\frac{-21}{2}\)
\(\frac{-22}{2} \le \frac{-21}{2} \le \frac{-20}{2}\)
\(-11 \le \frac{-21}{2} \le -10\)
\(-21π-(-11)\times 2\pi=-21\pi+22\pi=\pi\in]-\pi ;\pi](A'_1)\)
\(-21π-(-10)\times 2\pi=-21\pi+20\pi=-\pi\notin]-\pi ;\pi]\)
3.
\(\frac{-9\pi}{4}=\frac{-8\pi}{4}+\frac{-\pi}{4}=-2\pi+\frac{-\pi}{4}\mapsto\frac{-\pi}{4}\in]-\pi ;\pi](A'_2)\)
4.
\(\frac{\frac{-17\pi}{3}}{2\pi}=\frac{-17\pi}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-17\pi}{3}}{2\pi}=\frac{-17\pi}{6\pi}\)
\(\iff \frac{\frac{-17\pi}{3}}{2\pi}=\frac{-17}{6}\)
\(\frac{-18}{6}\le \frac{-17}{6}\le \frac{-12}{6}\)
\(\iff -3 \le \frac{-17}{6}\le -2\)
\(\frac{-17\pi}{3}-(-3) \times 2\pi=\frac{-17\pi}{3}+3 \times 2\pi\)
\(\iff \frac{-17\pi}{3}-(-3) \times 2\pi=\frac{-17\pi}{3}+6\pi\)
\(\iff \frac{-17\pi}{3}-(-3) \times 2\pi=\frac{-17\pi}{3}+\frac{18\pi}{3}\)
\(\iff \frac{-17\pi}{3}-(-3) \times 2\pi=\frac{\pi}{3}\in]-\pi ;\pi](A'_3)\)
\(\frac{-17\pi}{3}-(-2) \times 2\pi=\frac{-17\pi}{3}+2 \times 2\pi\)
\(\iff \frac{-17\pi}{3}-(-2) \times 2\pi=\frac{-17\pi}{3}+4\pi\)
\(\iff \frac{-17\pi}{3}-(-2) \times 2\pi=\frac{-17\pi}{3}+\frac{12\pi}{3}\)
\(\iff \frac{-17\pi}{3}-(-2) \times 2\pi=\frac{-5\pi}{3}\notin]-\pi ;\pi]\)
5.\(\frac{17\pi}{6}\)
\(\frac{\frac{17\pi}{6}}{2\pi}=\frac{17\pi}{6} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{17\pi}{6}}{2\pi}=\frac{17\pi}{12\pi}\)
\(\iff \frac{\frac{17\pi}{6}}{2\pi}=\frac{17}{12}\)
\(\frac{12}{12}\le \frac{17}{12}\le \frac{24}{12}\)
\(\iff 1 \le \frac{17}{12}\le 2\)
\(\frac{17\pi}{6}-2\pi\)
\(=\frac{17\pi}{6}-\frac{12\pi}{6}\)
\(=\frac{5\pi}{6}\in]-\pi ;\pi](A'_4)\)
\(\frac{17\pi}{6}-2\times 2\pi\)
\(=\frac{17\pi}{6}-4\pi\)
\(=\frac{17\pi}{6}-\frac{24\pi}{6}\)
\(=\frac{-7\pi}{6}\notin]-\pi ;\pi]\)
6.\(\frac{-121\pi}{3}\)
\(\frac{\frac{-121\pi}{3}}{2\pi}=\frac{-121\pi}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-121\pi}{3}}{2\pi}=\frac{-121\pi}{6\pi}\)
\(\iff \frac{\frac{-121\pi}{3}}{2\pi}=\frac{-121}{6}\)
\(\frac{-126}{6} \le \frac{-121}{6} \le \frac{-120}{6}\)
\(-21 \le \frac{-121}{6} \le -20\)
\(\frac{-121\pi}{3}-(-21)\times 2\pi=\frac{-121\pi}{3}+42\pi\)
\(\iff \frac{-121\pi}{3}-(-21)\times 2\pi=\frac{-121\pi}{3}+\frac{126\pi}{3}\)
\(\iff \frac{-121\pi}{3}-(-21)\times 2\pi=\frac{5\pi}{3}\notin]-\pi ;\pi]\)
\(\frac{-121\pi}{3}-(-20)\times 2\pi=\frac{-121\pi}{3}+40\pi\)
\(\iff \frac{-121\pi}{3}-(-20)\times 2\pi=\frac{-121\pi}{3}+\frac{120\pi}{3}\)
\(\iff \frac{-121\pi}{3}-(-20)\times 2\pi=\frac{-\pi}{3}\in]-\pi ;\pi](A'_5)\)