Exercice : Equation Trigonométrique Second Degré
Résoudre dans \(\mathbb{R}\) les équations suivantes :
Question
1. \(2cos^2 x+ 9 cos x+4=0\)
Solution
\(2cos^2 x+ 9 cos x+4=0\)
\(X=cos x\)
\(2X^2+ 9 X+4=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=9^2-4 \times 2 \times 4\)
\(\iff \Delta=81-32=49\)
Comme \(\Delta\)>0, l 'équation \(2X^2+ 9 X+4=0\)
admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-9-\sqrt{49}}{2\times 2}\\X_2=\frac{-9+\sqrt{49}}{2\times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-9-7}{4}\\X_2=\frac{-9+7}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-16}{4}\\X_2=\frac{-2}{4}\end{cases}\)
\(\iff \begin{cases}X_1=-4\\X_2=\frac{-1}{2}\end{cases}\)
\(\iff \begin{cases}cos x_1=-4\\cos x_2=\frac{-1}{2}\end{cases}\)
\(cos x_1=-4\) n'a pas de solution car \(cos x\in[-1 ;1]\).
\(cos x_2=\frac{-1}{2}\)
\(\begin{cases}x_2=\pi-\frac{\pi}{3}+2k\pi\\x_2=-(\pi-\frac{\pi}{3})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x_2=\frac{2\pi}{3}+2k\pi\\x_2=-\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Dans \(\mathbb{R}\), les solutions sont :
\(\iff \begin{cases}x_2=\frac{2\pi}{3}+2k\pi\\x_2=-\frac{2\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Dans \(]-\pi ;\pi]\) , les solutions sont :
\(\iff \begin{cases}x_2=\frac{2\pi}{3}\\x_2=-\frac{2\pi}{3}\end{cases}\)
Question
2. \(4sin^2 x- 2(1+\sqrt{3})sin x+\sqrt{3}=0\)
Solution
\(4sin^2 x- 2(1+\sqrt{3})sin x+\sqrt{3}=0\)
\(X=sin x\)
\(4X^2- 2(1+\sqrt{3})X+\sqrt{3}=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-2(1+\sqrt{3}))^2-4 \times 4 \times \sqrt{3}\)
\(\iff \Delta=4(1+\sqrt{3})^2-16\times \sqrt{3}\)
\(\iff \Delta=4(1^2+2\sqrt{3}+3)-16\times \sqrt{3}\)
\(\iff \Delta=4(4+2\sqrt{3})-16\times \sqrt{3}\)
\(\iff \Delta=4(4+2\sqrt{3})-16\times \sqrt{3}\)
\(\iff \Delta=16+8\sqrt{3}-16\sqrt{3}\)
\(\iff \Delta=16-8\sqrt{3}\)
\(\iff \Delta=4(4-2\sqrt{3})\)
\(\iff \Delta=4(1-2\sqrt{3}+3)\)
\(\iff \Delta=4(1^2-2\sqrt{3}+\sqrt{3}^2)\)
\(\iff \Delta=4(1-\sqrt{3})^2\)
Comme \(\Delta\)>0, l 'équation \(4X^2- 2(1+\sqrt{3})X+\sqrt{3}=0\)
admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-(- 2(1+\sqrt{3}))-\sqrt{4(1-\sqrt{3})^2}}{2\times 4}\\X_2=\frac{-(- 2(1+\sqrt{3}))+\sqrt{4(1-\sqrt{3})^2}}{2\times 4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{ 2(1+\sqrt{3})-2(1-\sqrt{3})}{8}\\X_2=\frac{2(1+\sqrt{3})+2(1-\sqrt{3})}{8}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{2+2\sqrt{3}-2+2\sqrt{3})}{8}\\X_2=\frac{2+2\sqrt{3}+2-2\sqrt{3}}{8}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{4\sqrt{3}}{8}\\X_2=\frac{4}{8}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{\sqrt{3}}{2}\\X_2=\frac{1}{2}\end{cases}\)
\(cos x_1=\frac{\sqrt{3}}{2}\)
\(\begin{cases}x_1=\frac{\pi}{6}+2k\pi\\x_1=-\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(cos x_2=\frac{1}{2}\)
\(\begin{cases}x_2=\frac{\pi}{3}+2k\pi\\x_2=-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Dans \(\mathbb{R}\), les solutions sont :
\(\begin{cases}\frac{\pi}{6}+2k\pi\\-\frac{\pi}{6}+2k\pi\\\frac{\pi}{3}+2k\pi\\-\frac{\pi}{3}+2k\pi\end{cases}\)
\(k\in\mathbb{Z}\)
Dans \(]-\pi ;\pi]\) , les solutions sont :
\(\begin{cases}-\frac{\pi}{3}\\-\frac{\pi}{6}\\\frac{\pi}{6}\\\frac{\pi}{3}\end{cases}\)
\(k\in\mathbb{Z}\)
Question
3.Déterminer les éventuelles racines du trinôme \(t\) défini par \(t(x)=-4x^2+(2\sqrt{3}-2)x+\sqrt{3}\)
Solution
\(\Delta=(2\sqrt{3}-2)^2-4\times (-4)\sqrt{3}\)
\(\Delta=4\sqrt{3}^2-2 \times 2\sqrt{3} \times 2+2^2+16\sqrt{3}\)
\(\iff \Delta=4\times 3-8\sqrt{3} +4+16\sqrt{3}\)
\(\iff \Delta=12+8\sqrt{3} +4\)
\(\iff \Delta=(2\sqrt{3})^2+2 \times 2\sqrt{3} \times 2+2^2\)
\(\iff \Delta=(2\sqrt{3}+2)^2\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(2\sqrt{3}-2)-(2\sqrt{3}+2)}{2 \times (-4)}\\x_2=\frac{-(2\sqrt{3}-2)+(2\sqrt{3}+2)}{2 \times (-4)}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-2\sqrt{3}+2-2\sqrt{3}-2)}{-8}\\x_2=\frac{-2\sqrt{3}+2+2\sqrt{3}+2)}{-8}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-4\sqrt{3}}{-8}\\x_2=\frac{4}{-8}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{\sqrt{3}}{2}\\x_2=\frac{-1}{2}\end{cases}\)
Question
2.Factoriser \(t(x)\)
Solution
La forme factorisée est :
\(t(x)=a(x-x_1)(x-x_2)\)
\(\iff t(x)=-4(x-\frac{\sqrt{3}}{2})(x-(\frac{-1}{2}))\)
\(\iff t(x)=-4(x-\frac{\sqrt{3}}{2})(x+\frac{1}{2}))\)
\(\iff t(x)=4(\frac{\sqrt{3}}{2}-x)(x+\frac{1}{2}))\)
\(\iff t(x)=(\sqrt{3}-2x)(2x+1)\)
\(\iff t(x)=(-2x+\sqrt{3})(2x+1)\)
Question
3.Etablir dans \([0 ;2\pi]\), le signe de \(2cos x+1\) et de \(-2cos x+\sqrt{3}\)
Solution
\(2cos x+1\ge 0\)
\(\iff cos x\ge \frac{-1}{2}\)
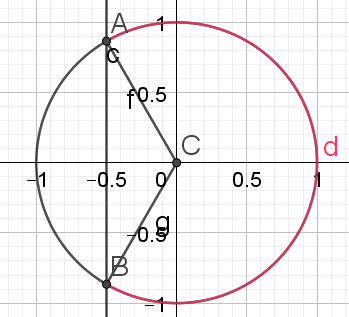
\(\iff x \in [0 ;\frac{2\pi}{3}] \cup [\frac{4\pi}{3} ;2\pi]\)
\(-2cos x+\sqrt{3}\ge 0\)
\(\iff -2cos x\ge -\sqrt{3}\)
\(\iff 2cos x\le \sqrt{3}\)
\(\iff cos x\le \frac{\sqrt{3}}{2}\)
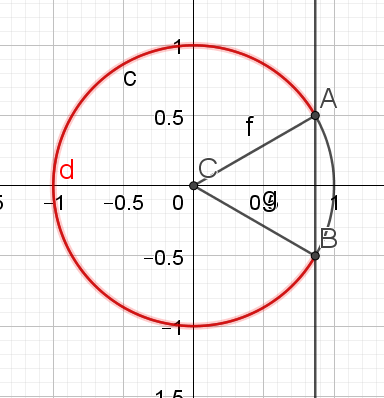
\(\iff x \in [\frac{\pi}{6} ;2\pi-\frac{\pi}{6}]=[\frac{\pi}{6} ;\frac{12\pi}{6}-\frac{\pi}{6}]\)
\(\iff x \in [\frac{\pi}{6} ;\frac{11\pi}{6}]\)
Question
4.En déduire le signe sur \([0 ;2\pi]\) de \(-4cos^2 x +(2\sqrt{3}-2) cos x +\sqrt{3}\)
