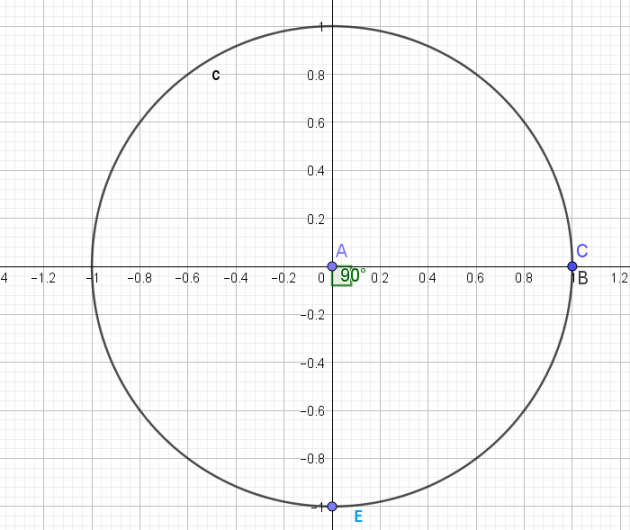
3. Construction d'angles
Fondamental :
Placer sur le cercle trigonométrique les points correspondants à des mesures d'angle de :
\(\frac{π}{4}\) ;\(\frac{π}{3}\); \(\frac{π}{6}\)
1. Construction de \(\frac{\pi}{4}\)(45°)
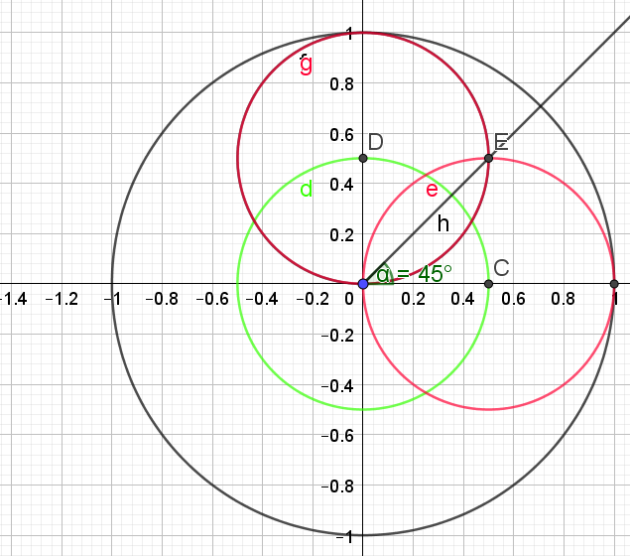
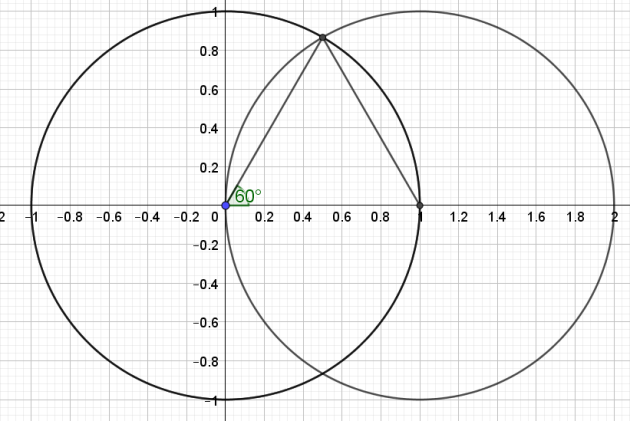
2. Construction de \(\frac{\pi}{3}\)(60°)
3. Construction de \(\frac{\pi}{6}\) (30°)
A partir de \(\frac{\pi}{3}\), on construit la bissectrice :
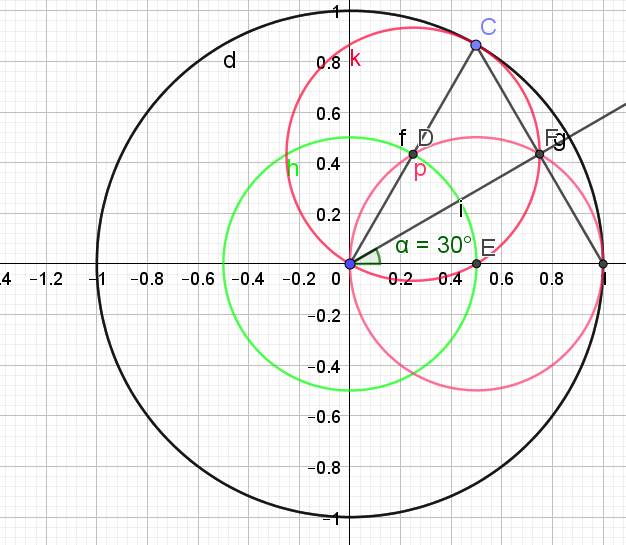
Fondamental :
Placer sur le cercle trigonométrique les points correspondants à des mesures d'angle de :
0 radian ;\(\frac{2π}{3}\);\(\frac{-π}{3}\) ;\(\frac{-π}{12}\);\(\frac{-π}{2}\) ;-π;2π
1. Construction de 0 radian
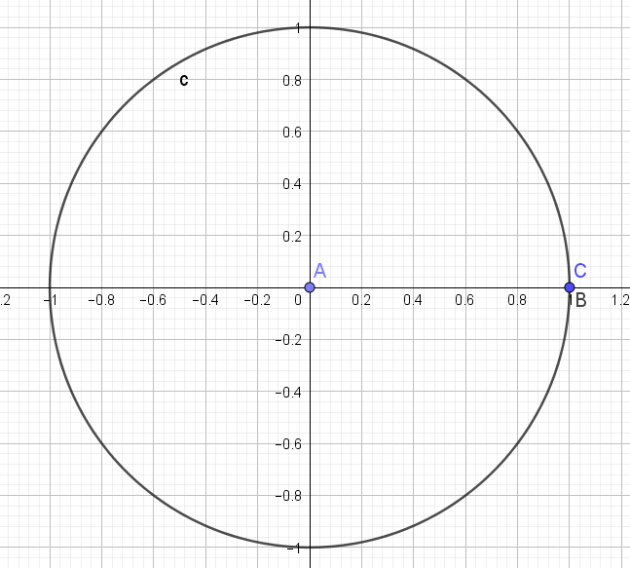
\(\widehat{BAC}=0 rad\)
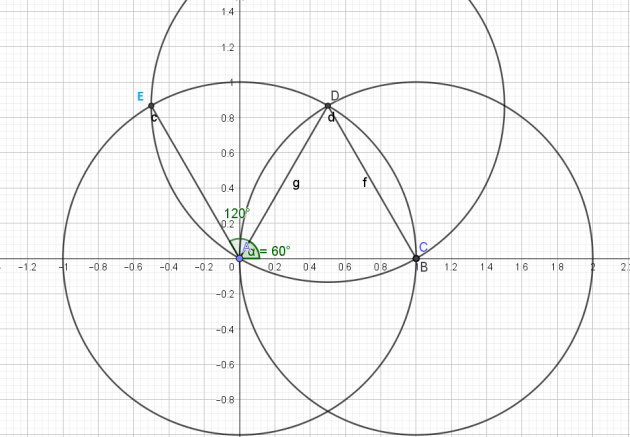
2.Construction de \(\frac{2π}{3}\) (120°)
\(\widehat{EAC}=\frac{2π}{3} rad\)
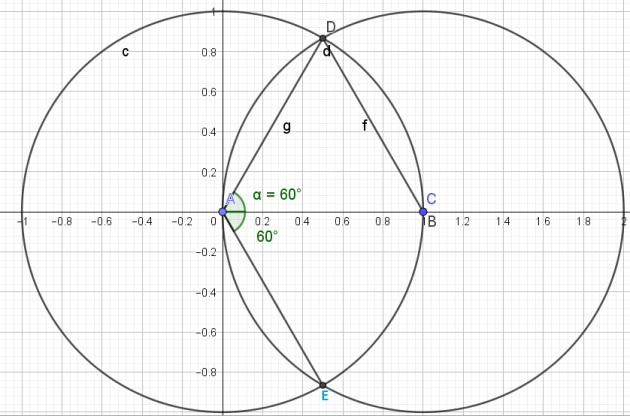
3. Construction de \(\frac{-π}{3}\) radian (-60°)
\(\widehat{CAE}=\frac{-π}{3} rad\)
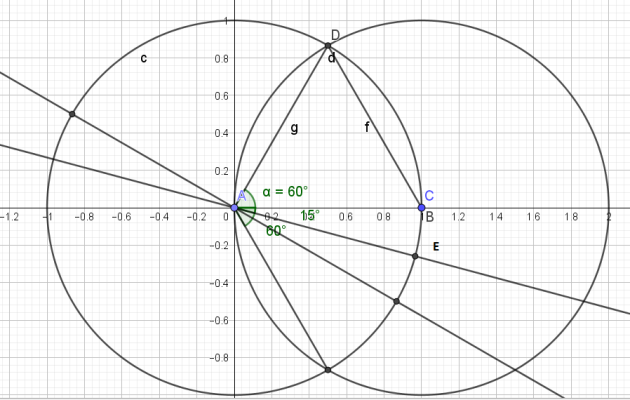
4. Construction de \(\frac{-π}{12}\) radian (-15°)
\(\widehat{CAE}=\frac{-π}{12}\)
5. Construction de \(\frac{-π}{2}\) radian (-90°)
\(\widehat{CAE}=\frac{-π}{2}\)