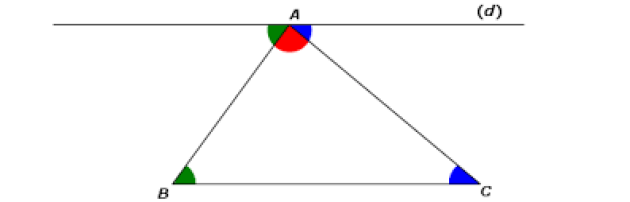
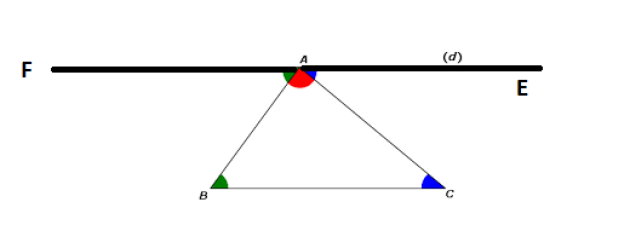
Somme des angles d'un triangle
Exemple :
Montrer que la somme des mesures (positives) des trois angles d'un triangle vaut 180°
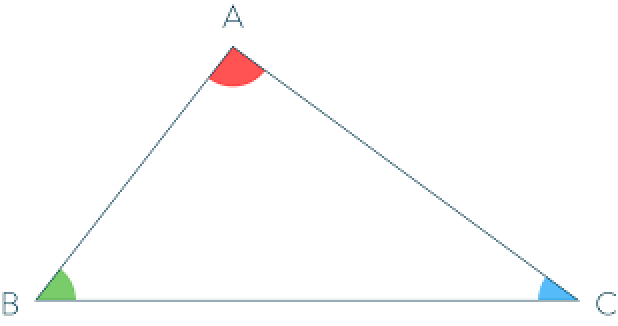
Complément :
\((\vec{BA} ;\vec{BC})+(\vec{CB} ;\vec{CA})+(\vec{AC} ;\vec{AB} )\)
\(=(-\vec{AB} ;-\vec{AF})+(\vec{CB} ;-\vec{AC})+(\vec{AC} ;\vec{AB} )\)
\(=(\vec{AC} ;\vec{AB} )+(\vec{AB} ;\vec{AF})+(\vec{CB} ;-\vec{AC})\)
\(=(\vec{AC};\vec{AF})+(\vec{AF} ;-\vec{AC})\)
\(=(\vec{AC};\vec{AF})+(\vec{AF} ;\vec{AC})+\pi\)
\(=(\vec{AC};\vec{AF})-(\vec{AC} ;\vec{AF})+\pi\)
\(=\pi\)
Exemple :
Dans la figure suivante, les deux droites (AB) et (DE) sont parallèles.
Déterminer la mesure de l'angle \((\vec{DC} ;\vec{DE} )\)
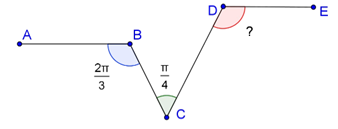
Complément :
\((\vec{BA} ;\vec{DE} )=-\pi\)
\((\vec{BA} ;\vec{DE} )=(\vec{BA} ;\vec{BC} )+(\vec{BC} ;\vec{DE})\)
\((\vec{BA} ;\vec{DE} )=(\vec{BA} ;\vec{BC} )+(\vec{BC} ;\vec{CD})+(\vec{CD} ;\vec{DE})\)
\((\vec{BA} ;\vec{DE} )=\frac{2\pi}{3}+(\vec{CB} ;\vec{CD})+\pi+(\vec{CD} ;\vec{DE})\)
\((\vec{BA} ;\vec{DE} )=\frac{2\pi}{3}+\frac{-\pi}{4}+\pi+(-\vec{DC} ;\vec{DE})\)
\((\vec{BA} ;\vec{DE} )=\frac{2\pi}{3}+\frac{-\pi}{4}+\pi+(\vec{DC} ;\vec{DE})+\pi\)
\(\iff -\pi=\frac{2\pi}{3}+\frac{-\pi}{4}+\pi+(\vec{DC} ;\vec{DE})+\pi\)
\(\iff -\pi=\frac{8\pi}{12}+\frac{-3\pi}{12}+(\vec{DC} ;\vec{DE})+2\pi\)
\(\iff -\pi=\frac{5\pi}{12}+(\vec{DC} ;\vec{DE})+2\pi\)
\(\iff \frac{5\pi}{12}+(\vec{DC} ;\vec{DE})+2\pi=-\pi\)
\(\iff (\vec{DC} ;\vec{DE})=-\frac{5\pi}{12}-3\pi\)
\(\iff (\vec{DC} ;\vec{DE})=\frac{12\pi}{12}-\frac{5\pi}{12}=\frac{7\pi}{12}\mapsto 7 \times 15=105°\)