VII/ Fonctions sinus et cosinus
Complément :
Fondamental :
\(\color{red}{\text{ Une fonction est dite pérodique, de période T si pour tout réel } x \text{ on a } f(x+T)=f(x)}\)
Exemple :
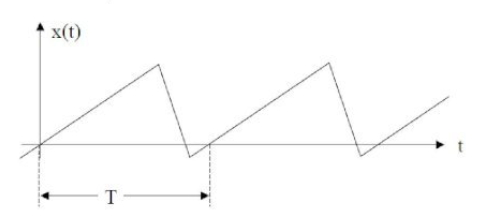
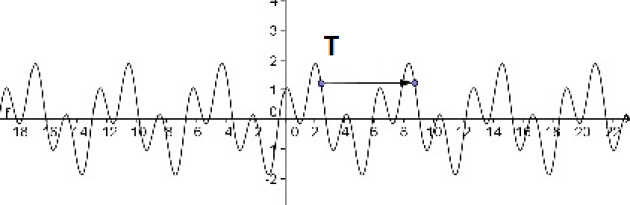
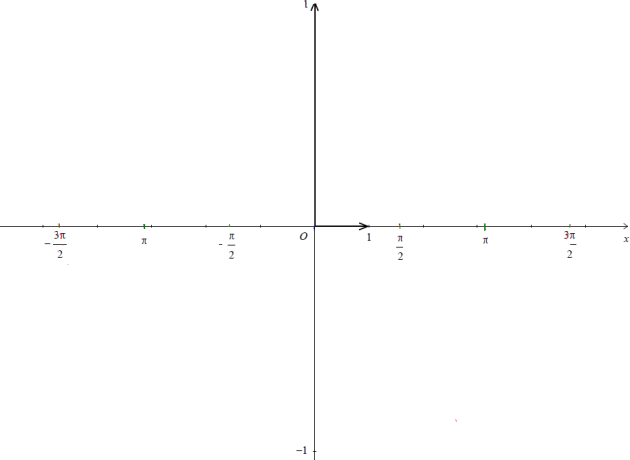
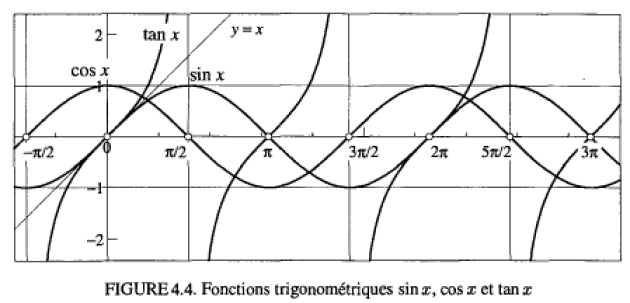
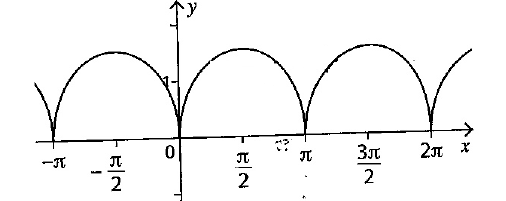
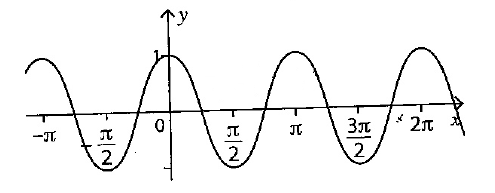
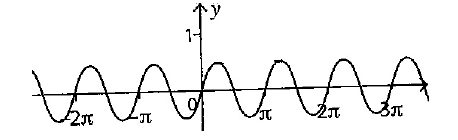
Dans chaque cas donnez la périodicité des fonctions ci-dessous :
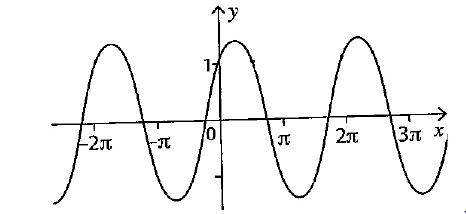
Complément :
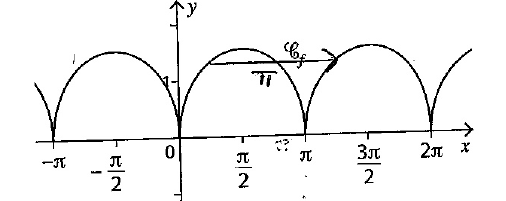
La période est \(\pi\)
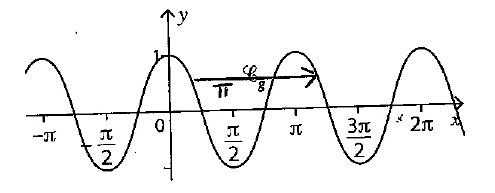
La période est \(\pi\)
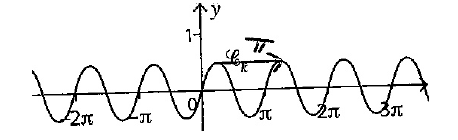
La période est \(\pi\)
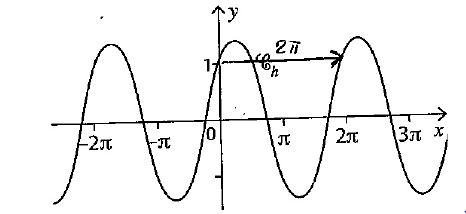
La période est \(2\pi\)
Remarque :
Si T est une période, tout multiple de T en est une autre.
\(...=f(x+2T)=f(x+T)=f(x)=f(x-T)=f(x-2T)=...\)
Fondamental :
Fondamental :
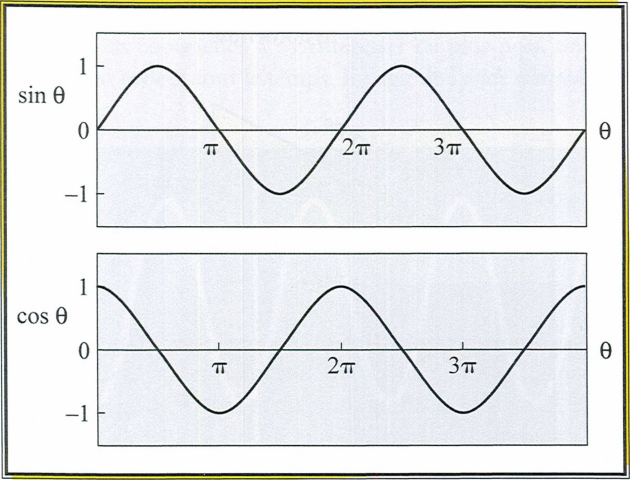
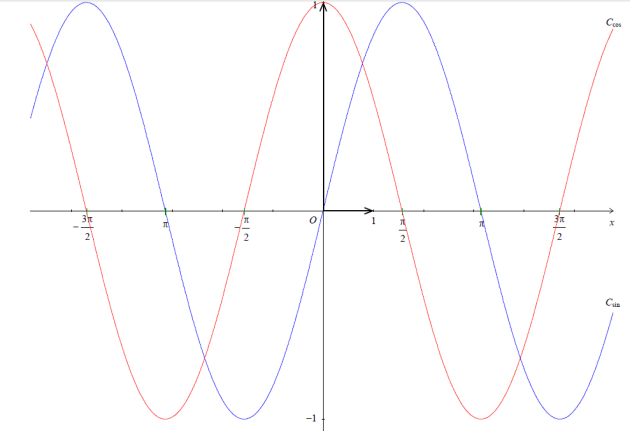
\(\color{red}{\text{Les fonctions cosinus et sinus sont périodiques de période }2\pi}\)
Fondamental :
\(\color{red}{\text{La fonction cosinus est paire.} f(-x)=f(x)}\)
La courbe est symétrique par rapport à l'axe des ordonnées.
\(\color{red}{\text{La fonction sinus est impaire} f(-x)=-f(x)}\)
La courbe est symétrique par rapport à l'origine du repère.
Exemple :
Dans chaque cas donnez la parité des fonctions ci-dessous :
Complément :
La fonction est paire car elle est symétrique par rapport à l'axe des ordonnées
La fonction est paire car elle est symétrique par rapport à l'axe des ordonnées
La fonction est impaire car elle est symétrique par rapport à l'origine du repère.
La fonction n'est ni paire, ni impaire car elle est symétrique par rapport à l'axe des ordonnées.
Complément :
Complément :
Exemple :
On considère la fonction définie sur \(\mathbb{R}\) par
\(f(x)=sin(2x)+cos(x)sin(x)\)
1.Montrer que la fonction \(f\) est périodique de période \(\pi\)
2.Déterminer la parité de la fonction \(f\)
Complément :
1.\(f(x+\pi)=sin(2(x+\pi))+cos(x+\pi)sin(x+\pi)\)
\(\iff f(x+\pi)=sin(2x+2\pi)+cos(x+\pi)sin(x+\pi)\)
or \(sin(x+2\pi)=sin(x)\) car la fonction sinus est \(2\pi\) périodique.
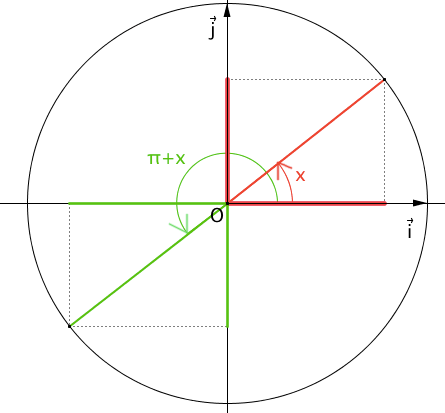
\(\begin{cases}cos(x+\pi)=-cos(x)\\sin(x+\pi)=-sin(x) \end{cases}\)
\(\iff f(x+\pi)=sin(2x)+(-cos(x))(-sin(x))\)
\(\iff f(x+\pi)=sin(2x)+cos(x)sin(x)\)
\(\iff f(x+\pi)=f(x)\)
donc la fonction \(f\) est périodique de période \(2\pi\)
2.\(f(-x)=sin(2(-x))+cos(-x)sin(-x)\)
\(\iff f(-x)=sin(-2x)+cos(-x)sin(-x)\)
\(\iff f(-x)=sin(-2x)+cos(-x)sin(-x)\)
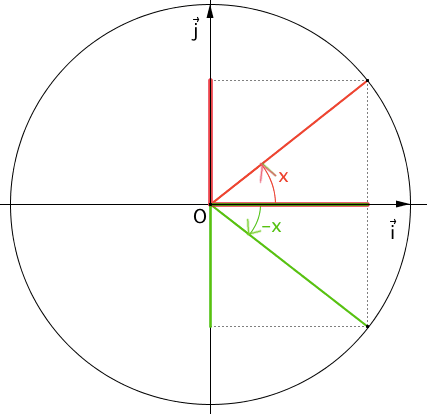
\(\begin{cases}cos(-x)=cos(x)\\sin(-x)=-sin(x) \end{cases}\)
\(\iff f(-x)=-sin(2x)+cos(x)(-sin(x))\)
\(\iff f(-x)=-sin(2x)-cos(x)sin(x)\)
\(\iff f(-x)=-(sin(2x)+cos(x)sin(x))\)
\(\iff f(-x)=-f(x)\)
la fonction \(f\) est donc impaire et symétrique par rapport à l'origine du repère.
Exemple : .
