III/ Mesure d'un angle orienté de vecteurs
Définition :
\(\color{red}{\text{Une mesure de l'angle orienté des vecteurs } \vec{u} \; et \; \vec{v} \; est \; y – x.}\)
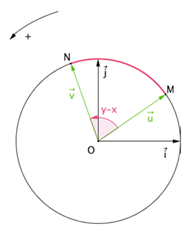
Fondamental : Propriété
Donc \((\vec{u} ;\vec{v})=-(\vec{v} ;\vec{u})\)
Exemple :
\((\vec{OB},\vec{OM})=\frac{\pi}{4}\)
\((\vec{OB},\vec{OP})=\frac{2\pi}{3}\)
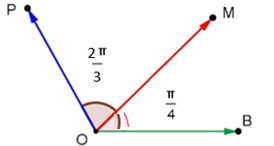
Déterminer une mesure de l'angle de vecteurs \((\vec{OM} ;\vec{OP} ) \)
Complément :
\((\vec{OM},\vec{OP})=\frac{2\pi}{3}-\frac{\pi}{4}\)
\((\vec{OM},\vec{OP})=\frac{8\pi}{12}-\frac{3\pi}{12}=\frac{5\pi}{12}\)