Exercice : Rappel :Différentes Méthodes de calcul du produit scalaire
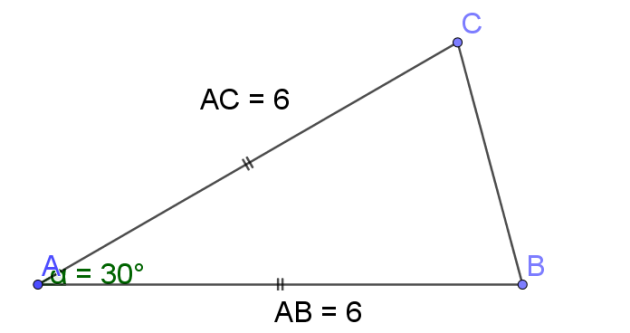
\(\color{magenta}{\textbf{1.Déterminer le produit scalaire } \vec{AB}\cdot\vec{AC} \textbf{( à l'aide de la formule de base)}}\)
Question
Solution
1.a.\(\vec{AB}\cdot\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})=AB \times AC \times cos(\widehat{BAC})\)
\(\vec{AB}\cdot\vec{AC}=6 \times 6 \times cos(30°)\)
\(\vec{AB}\cdot\vec{AC}=6 \times 6 \times cos(\frac{\pi}{6})\)
\(\vec{AB}\cdot\vec{AC}=6 \times 6 \times \frac{\sqrt{3}}{2}\)
\(\vec{AB}\cdot\vec{AC}=18\sqrt{3}\)
Question
\(\color{magenta}{ \textbf{ 2. Déterminer le produit scalaire } \vec{AB}\cdot\vec{AC} \textbf{ par projection }}\)
Solution

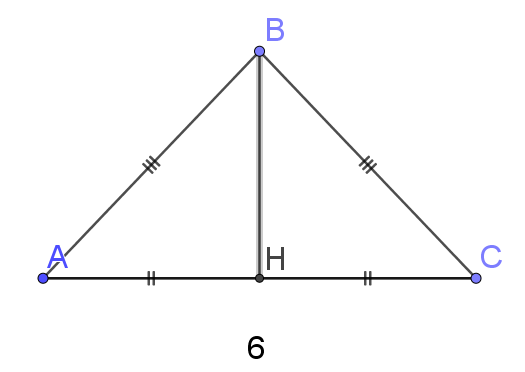
b.\(\vec{AB}\cdot\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})=AB \times AC \times cos(\widehat{BAC})=AC \times AH\)
en effet dans le triangle AHB rectangle en H
\(cos(\widehat{BAH})=cos(\widehat{BAC})=\frac{côté adjacent}{hypoténuse}=\frac{AH}{AB}\) donc \(AH=AB \times cos(\widehat{BAC})\)
finalement :
\(\vec{AB}\cdot\vec{AC}=6 \times 3=18\)
Question
\(\color{magenta}{ \textbf{ 3. Déterminer le produit scalaire } \vec{AB}\cdot\vec{AC} \textbf{ à l'aide des coordonnées des vecteurs}}\)
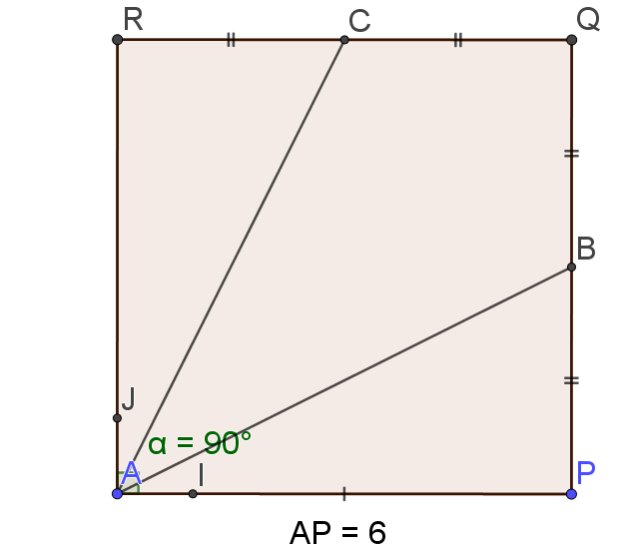
Soit (A ;I ;J) le repère orthonormé représenté ci-dessus :
1.Donner les coordonnées des points A,B, C dans ce repère.
2.En déduire les coordonnées des vecteurs \(\vec{AB}\) et \(\vec{AC}\)
3.En déduire la valeur du produit scalaire \(\vec{AB} \cdot \vec{AC}\)
Solution
1.Dans le repère \((A,\vec{AI},\vec{AJ})\) , les coordonnées des points sont :
A(0 ;0)
B(6 ;3)
C(3 ;6)
2.\(\vec{AB}=\begin{pmatrix}6-0\\3-0\end{pmatrix}=\begin{pmatrix}6\\3\end{pmatrix}\)
\(\vec{AC}=\begin{pmatrix}3-0\\6-0\end{pmatrix}=\begin{pmatrix}3\\6\end{pmatrix}\)
\(\vec{AB}\cdot\vec{AC}=xx'+yy'=6\times 3+3\times 6=18+18=36\)