Exercice : Angles Vecteurs
On considère le plan muni d'un repère orthonormal (O ;I ;J)
Question
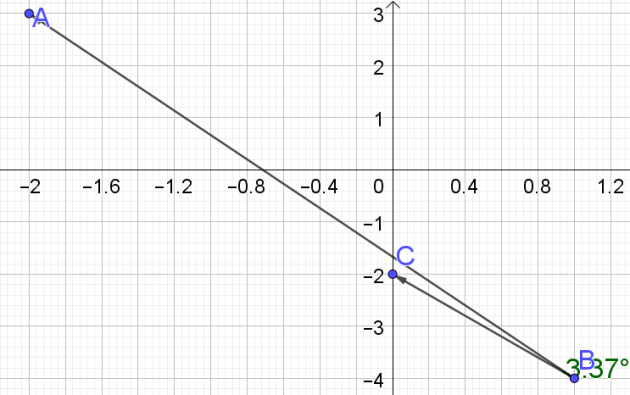
1. Soit A,B,C trois points du plan de coordonnées respectives (-2 ;3) ,(1 ;-4) et (0 ;-2)
a.Déterminer le produit scalaire de \(\vec{BA}\cdot\vec{BC}\),\(\|\vec{BA}\|\) et\( \|\vec{BC}\|\)
Solution
\(\vec{BA}=\begin{pmatrix}-2-1\\3-(-4)\end{pmatrix}=\begin{pmatrix}-3\\7\end{pmatrix}\)
\(\vec{BC}=\begin{pmatrix}0-1\\-2-(-4)\end{pmatrix}=\begin{pmatrix}-1\\2\end{pmatrix}\)
\(\vec{BA}\cdot\vec{BC}=(-3)\times(-1)+7\times2=3+14=17\)
\(\|\vec{BA}\|=\sqrt{(-3)^2+7^2}=\sqrt{9+49}=\sqrt{58}\)
\(\|\vec{BC}\|=\sqrt{(-1)^2+2^2}=\sqrt{1+4}=\sqrt{5}\)
Question
b. En déduire la mesure de l'angle géométrique \(\widehat{ABC}\) au centième près de degrés.
Solution
\(\vec{BA}\cdot\vec{BC}=BA \times BC \times cos((\vec{BA},\vec{BC}))=17\)
donc \(\sqrt{58} \times \sqrt{5} \times cos((\vec{BA},\vec{BC}))=17\)
\(cos((\vec{BA},\vec{BC}))=\frac{17}{\sqrt{58} \times \sqrt{5}}\simeq 3,4°\)