Exercice : Angles vecteurs 2
Question
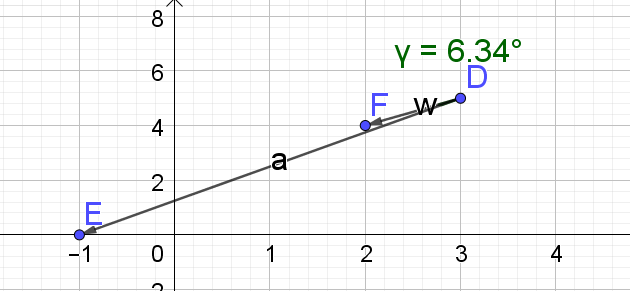
Donner une mesure de l'angle orienté \((\vec{DE},\vec{DF})\) où D(3 ;5),E(-1 ;0), F(2 ;4) au centième de degré près.
Solution
D(3 ;5),E(-1 ;0), F(2 ;4)
\(\vec{DE}=\begin{pmatrix}-1-3\\0-5\end{pmatrix}=\begin{pmatrix}-4\\-5\end{pmatrix}\)
\(\vec{DF}=\begin{pmatrix}2-3\\4-5\end{pmatrix}=\begin{pmatrix}-1\\-1\end{pmatrix}\)
\(\vec{DE}\cdot\vec{DF}=(-4)\times(-1)+(-5)\times(-1)=4+5=9\)
\(\|\vec{DE}\|=\sqrt{(-4)^2+(-5)^2}=\sqrt{16+25}=\sqrt{41}\)
\(\|\vec{DF}\|=\sqrt{(-1)^2+(-1)^2}=\sqrt{1+1}=\sqrt{2}\)
\(\vec{DE}\cdot\vec{DF}=DE \times DF \times cos((\vec{DE},\vec{DF}))=9\)
donc \(\sqrt{41} \times \sqrt{2} \times cos((\vec{DE},\vec{DF}))=9\)
\(cos((\vec{DE},\vec{DF}))=\frac{9}{\sqrt{41} \times \sqrt{2}}\simeq 6,3°\)