Exercice : Droites Perpendiculaires
On considère le plan muni d'un repère (O ;I ;J) orthonormé.
1.Dans chaque cas déterminer une équation cartésienne de la droite perpendiculaire au vecteur \(\vec{u}\) et passant par le point A :
Question
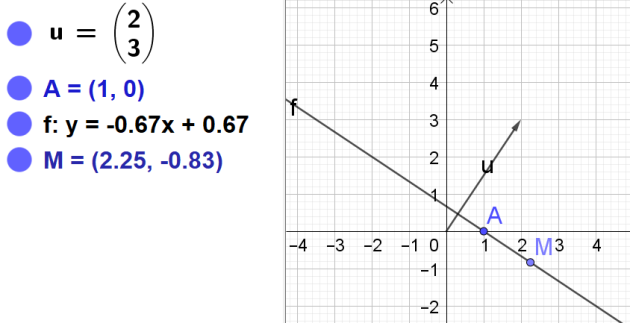
a. \(\vec{u}=\begin{pmatrix}2\\3\end{pmatrix}\) et A(1 ;0)
Solution
Soit M\((x,y)\) un point appartenant à la perpendiculaire au vecteur \(\vec{u}\) au point A :
\(\vec{AM}=\begin{pmatrix}x-1\\y-0\end{pmatrix}\)
\(\vec{u}=\begin{pmatrix}2\\3\end{pmatrix}\)
\(\vec{AM}\cdot\vec{u}=2(x-1)+3(y-0)=2x-2+3y=0\)
d'où \(2x-2+3y=0\)
donc l'équation de la droite est \(y=\frac{-2}{3}x+\frac{2}{3}\)
Question
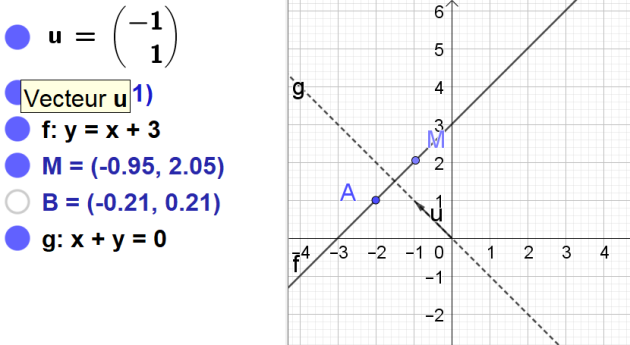
b. \(\vec{u}=\begin{pmatrix}-1\\1\end{pmatrix}\) et A(-2 ;1)
Solution
Soit M\((x,y)\) un point appartenant à la perpendiculaire au vecteur \(\vec{u}\) au point A :
\(\vec{AM}=\begin{pmatrix}x-(-2)\\y-1\end{pmatrix}\)\(=\begin{pmatrix}x+2\\y-1\end{pmatrix}\)
\(\vec{u}=\begin{pmatrix}-1\\1\end{pmatrix}\)
\(\vec{AM}\cdot\vec{u}=-1(x+2)+1(y-1)=-x-2+y-1=0\)
d'où \(-x+y-3=0\)
donc l'équation de la droite est \(y=x+3\)