Exercice : Calcul d'angles
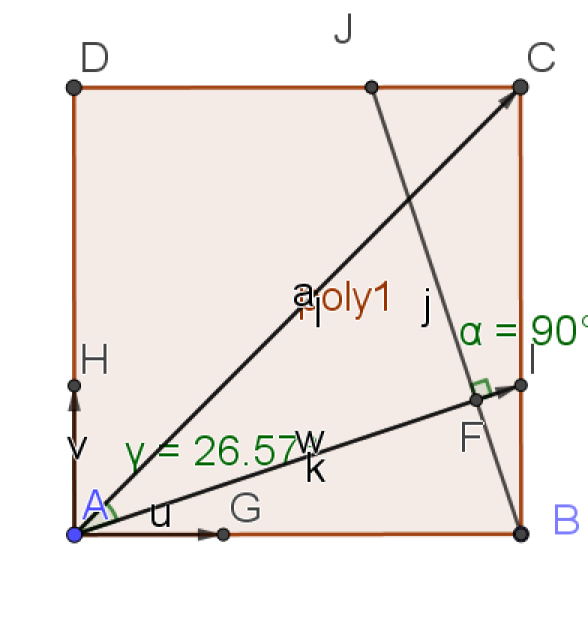
ABCD est un carré de côté 3. I et J sont les points tels que \(\vec{BI}=\frac{1}{3}\vec{BC}\) et \(\vec{CJ}=\frac{1}{3}\vec{CD}\).
\(\color{red}{\textbf{• Le but de la partie A est de montrer que les droites (AI) et (BJ) sont perpendiculaires.}}\)
\(\color{red}{\textbf{• Le but de la partie B est de déterminer une mesure de l'angle }} \widehat{AIC}.\)
Question
\(\color{magenta}{\textbf{Partie A}}\)
1. Calculer \(\overrightarrow{AI}\centerdot\overrightarrow{BJ}.\)
On pourra remarquer que \(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}\) et que \(\overrightarrow{BJ}=\overrightarrow{BC}+\overrightarrow{CJ}\).
Solution
\(\overrightarrow{AI}\centerdot\overrightarrow{BJ}=(\overrightarrow{AB}+\overrightarrow{BI})\cdot(\overrightarrow{BC}+\overrightarrow{CJ})\)
\(\overrightarrow{AI}\centerdot\overrightarrow{BJ}=\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{AB}\cdot\overrightarrow{CJ}+\overrightarrow{BI}\cdot\overrightarrow{BC}+\overrightarrow{BI}\cdot\overrightarrow{CJ}\)
or \(\begin{cases}\overrightarrow{AB}\cdot\overrightarrow{BC}=0 car les deux vecteurs \overrightarrow{AB} et \overrightarrow{BC} sont orthogonaux.\\\overrightarrow{AB}\cdot\overrightarrow{CJ}=AB \times CJ \times cos(\pi)=3 \times 1 \times (-1)=-3\\\overrightarrow{BI}\cdot\overrightarrow{BC}=BI \times BC \times cos(0)=3 \times 1 \times 1=3\\\overrightarrow{BI}\cdot\overrightarrow{CJ}=0 car les deux vecteurs \overrightarrow{BI} et \overrightarrow{CJ} sont orthogonaux.\end{cases}\)
donc
\(\overrightarrow{AI}\centerdot\overrightarrow{BJ}=0\)
Question
\(2. Conclure.\)
Solution
On en déduit que les vecteurs \(\overrightarrow{AI}\) et \(\overrightarrow{BJ}\) sont orthogonaux et donc les droites (AI) et (BJ) sont perpendiculaires.
\(\color{magenta}{\textbf{Partie B}}\)
Question
\(\color{magenta}{\textbf{Partie B}}\)
1. a. Calculer rapidement les longueurs AI et AC.
Solution
Dans le triangle ABI rectangle en B :
\(AI^2=AB^2+BI^2\)
\(AI^2=3^2+1^2=9+1=10\)
donc \(AI=\sqrt{10}\)
Dans le triangle ABC rectangle en B :
\(AC^2=AB^2+BC^2\)
\(AC^2=3^2+3^2=9+9=18\)
donc \(AC=\sqrt{18}\)
Question
b. En déduire l'expression de \(\overrightarrow{AI}\cdot\overrightarrow{AC}\) en fonction de \(cos(\widehat{IAC})\)
Indice
\(\overrightarrow{AI}\cdot\overrightarrow{AC}=AI \times AC \times cos(\widehat{IAC})\)
\(\overrightarrow{AI}\cdot\overrightarrow{AC}=\sqrt{10} \times \sqrt{18} \times cos(\widehat{IAC})\)
Question
2. On considère le repère \((A,\frac{\overrightarrow{AB}}{3},\frac{\overrightarrow{AD}}{3})\).
a. Pourquoi ce repère est-il orthonormal ?
Solution
Le repère \((A,\frac{\overrightarrow{AB}}{3},\frac{\overrightarrow{AD}}{3})\) est orthonormal car
les vecteurs \(\frac{\overrightarrow{AB}}{3}\) et \(\frac{\overrightarrow{AD}}{3}\) sont orthogonaux et de même longueur.
Question
b. Sans justifier, donner les coordonnées des points A,B,C,D,I et J.
Solution
A(0,0),B(3,0),C(3,3), D(0,3) ,I(3,1) et J(2,3)
Question
c. Calculer \(\overrightarrow{AI}\cdot\overrightarrow{AC}\)
Solution
\(\overrightarrow{AI}=\begin{pmatrix}3-0\\1-0\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}\)
\(\overrightarrow{AC}=\begin{pmatrix}3-0\\3-0\end{pmatrix}=\begin{pmatrix}3\\3\end{pmatrix}\)
\(\overrightarrow{AI}\cdot\overrightarrow{AC}=3\times3+1\times 3=12\)
Question
3. Déduire de ces deux questions une mesure approchée de l'angle \(\). On arrondira au dixième.
Solution
\(\sqrt{10} \times \sqrt{18} \times cos(\widehat{IAC})=12\)
\(cos(\widehat{IAC})=\frac{12}{\sqrt{10} \times \sqrt{18}}\)
\(\widehat{IAC}=Arccos(\frac{12}{\sqrt{10} \times \sqrt{18}})\)
\(\widehat{IAC}\simeq26,57\)°