Exercice : Projection 2
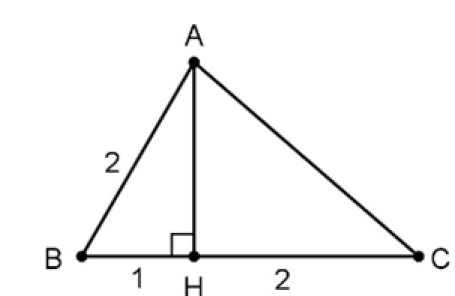
En utilisant les renseignements portés sur la figure ci-contre, calculer les produits scalaires suivants :
Question
a.\((\vec{AB}+\vec{AH})\cdot\vec{AB}\)
Solution
a. \((\vec{AB}+\vec{AH})\cdot\vec{AB}=\vec{AB}\cdot\vec{AB}+\vec{AH}\cdot\vec{AB}\)
or \(\vec{AB}\cdot\vec{AB}=AB \times AB \times cos((\vec{AB},\vec{AB}))=AB \times AB \times cos(0)=AB^2=2^2=4\)
\(\vec{AH}\cdot\vec{AB}=AH \cdot\ AH\) car B se projette orthogonalement en H sur (AH)
\(\vec{AH}\cdot\vec{AB}=AH \times AH \times cos((\vec{AH},\vec{AH}))\)
\(\vec{AH}\cdot\vec{AB}=AH \times AH \times cos(0)\)
\(\vec{AH}\cdot\vec{AB}=AH \times AH\)
\(\vec{AH}\cdot\vec{AB}=AH^2\)
En utilisant le théorème de Pythagore dans le triangle rectangle AHB rectangle en H :
\(AH^2+HB^2=AB^2\)
\(AH^2+1^2=2^2\)
\(AH^2+1=4\)
\(AH^2=4-1=3\)
\(\vec{AH}\cdot\vec{AB}=3\)
\((\vec{AB}+\vec{AH})\cdot\vec{AB}=AB^2+AH^2=4+3=7\)
donc \(\color{red}{(\vec{AB}+\vec{AH})\cdot\vec{AB}=7}\)
Question
b.\((\vec{AH}+\vec{HC})\cdot\vec{AB}\)
Solution
b.\((\vec{AH}+\vec{HC})\cdot\vec{AB}=\vec{AH}\cdot\vec{AB}+\vec{HC}\cdot\vec{AB}\)
\(\vec{AH}\cdot\vec{AB}=3\)
\(\vec{HC}\cdot\vec{AB}=\vec{HC}\cdot\vec{HB}\) car \(\vec{AB}\) se projette sur (HC) en \(\vec{HB}\)
\(\vec{HC}\cdot\vec{AB}=\vec{HC}\cdot\vec{HB}=HC \times HB \times cos(\pi)=2 \times 1 \times (-1)=-2\)
\((\vec{AH}+\vec{HC})\cdot\vec{AB}=3-2=1\)
donc \(\color{red}{(\vec{AH}+\vec{HC})\cdot\vec{AB}=1}\)
\(\color{magenta}{Remarque :}\) \((\vec{AH}+\vec{HC})\cdot\vec{AB}\)=\(\vec{AC}\cdot\vec{AB}=1\) par la relation de Chasles.
Question
c.\((\vec{AH}+\vec{HB})\cdot(\vec{AH}+\vec{HC})\)
Solution
c.\( (\vec{AH}+\vec{HB})\cdot(\vec{AH}+\vec{HC})=\vec{AH}\cdot\vec{AH}+\vec{AH}\cdot\vec{HC}+\vec{HB}\cdot\vec{AH}+\vec{HB}\cdot\vec{HC}\)
\(\vec{AH}\cdot\vec{AH}=AH \times AH \times cos(\vec{AH},\vec{AH})=AH^2 \times cos(0)=AH^2\)
\(\vec{AH}\cdot\vec{HC}=0\) car les vecteurs \(\vec{AH}\) et \(\vec{HC}\) sont orthogonaux.
\(\vec{HB}\cdot\vec{AH}=0\) car les vecteurs \(\vec{HB}\) et \(\vec{AH}\) sont orthogonaux.
\(\vec{HB}\cdot\vec{HC}=HB \times HC \times cos(\pi)=1 \times 2 \times (-1)=-2\)
donc \((\color{red}{\vec{(AH}+\vec{HB})\cdot(\vec{AH}+\vec{HC})=3-2=1}\)
\(\color{magenta}{Remarque :}\) \((\vec{AH}+\vec{HB})\cdot(\vec{AH}+\vec{HC})\)=\(\vec{AB}\cdot\vec{AC}=1\) par la relation de Chasles.
Résultat déjà trouvé au b.