Exercice : Projections
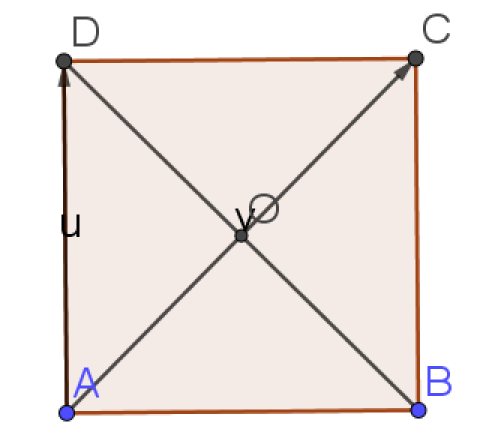
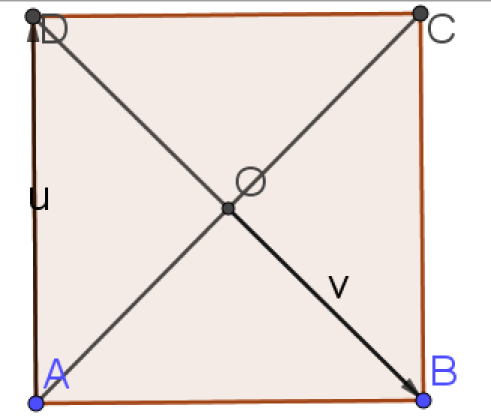
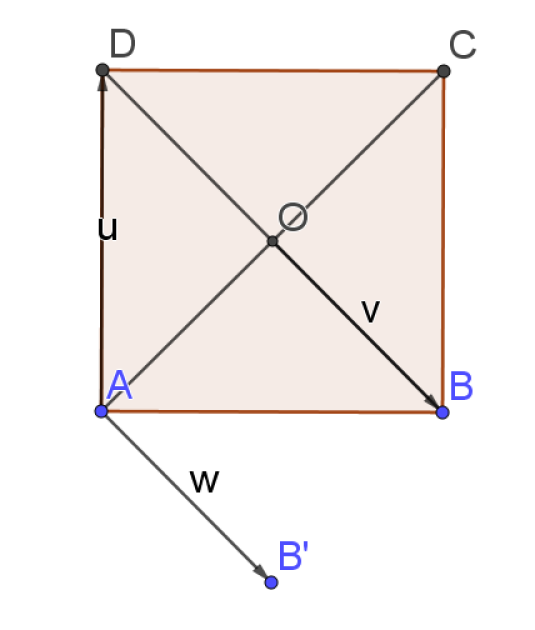
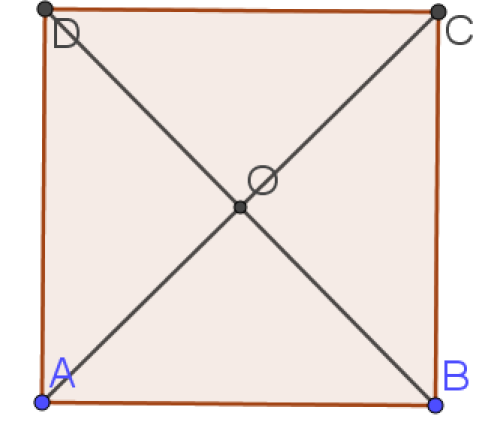
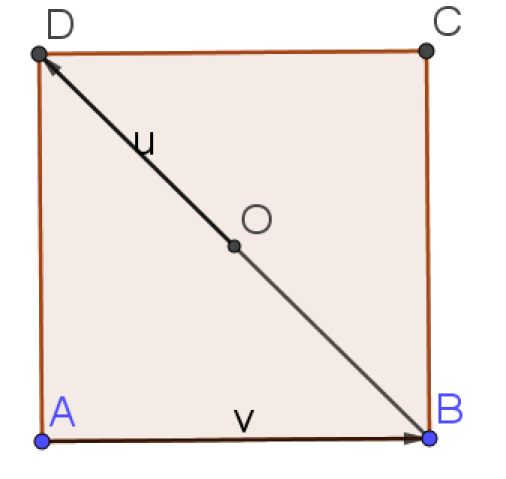
ABCD est un carré de centre O et de coté 4
Calculer :
Question
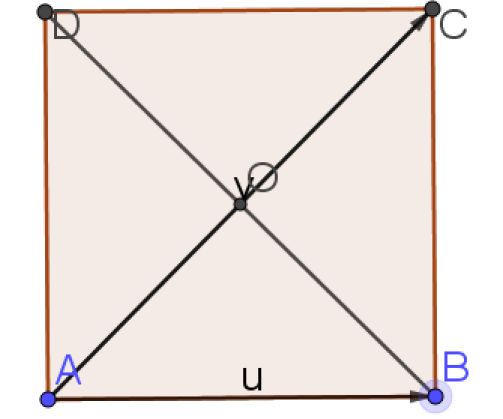
a. \(\vec{AB}\cdot\vec{AC}\)
Solution
a. \(\vec{AB}\cdot\vec{AC}=\)a. \(\vec{AB}\cdot\vec{AB}=AB \times AB=4 \times 4=16\) car C se projette orthogonalement en B sur (AB)
Question
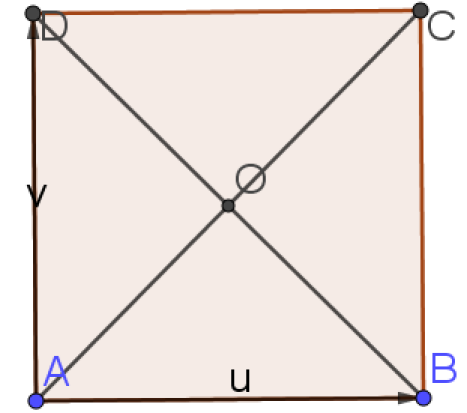
b. \(\vec{AB}\cdot\vec{AD}\)\(\)
Solution
b. \(\vec{AB}\cdot\vec{AD}=0\) car les vecteurs sont orthogonaux
Question
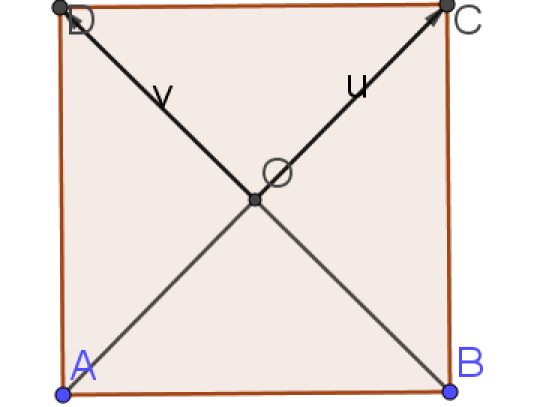
c. \(\vec{OC}\cdot\vec{OD}\)\(\)
Solution
c. \(\vec{OC}\cdot\vec{OD}\)\(=0\) car les vecteurs sont orthogonaux
Question
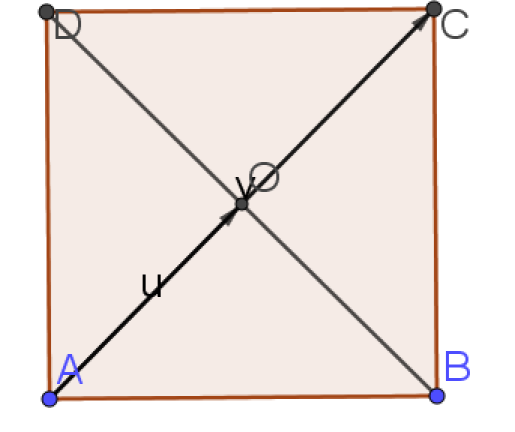
d. \(\vec{AC}\cdot\vec{AO}\)
Solution
d. \(\vec{AC}\cdot\vec{AO}=AC \times AO \times cos(0)\)
Calcul de la longueur AC grâce au théorème de Pythagore dans le triangle ABC rectangle en B:
\(AC^2=AB^2+BC^2=a^2+a^2=2a^2\)
\(AC=\sqrt{2a^2}=\sqrt{2}a\)
donc \(\color{magenta}{\textbf{La longueur de la diagonale d'un carré est la longueur du côté multipliée par }\sqrt{2}}\)
donc dans notre cas : \(AC=4\sqrt{2}\)
d'où \(\vec{AC}\cdot\vec{AO}= 4\sqrt{2} \times 2\sqrt{2} \times cos(0)=8\sqrt{2}^2=8 \times 2=16\)
Question
e. \(\vec{OC}\cdot\vec{OA}\)\(\)
Solution
e. \(\vec{OC}\cdot\vec{OA}\)
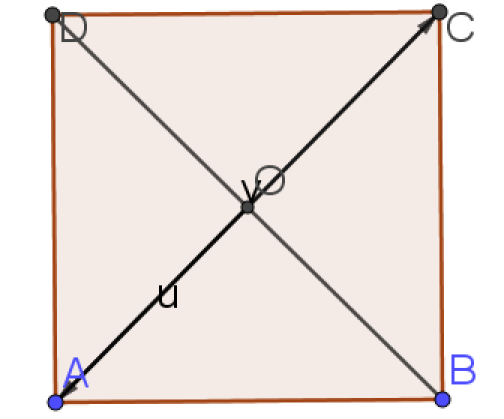
\(\vec{OC}\cdot\vec{OA}= OC \times OA \times cos(\pi)=OC \times OA \times (-1)=-OC \times OA=-2\sqrt{2} \times 2\sqrt{2}=-4\sqrt{2}^2=-4 \times 2=-8\)
Question
f. \(\vec{AD}\cdot\vec{OB}\)
Question
g. \(\vec{AB}\cdot\vec{AO}\)\(\)
Solution
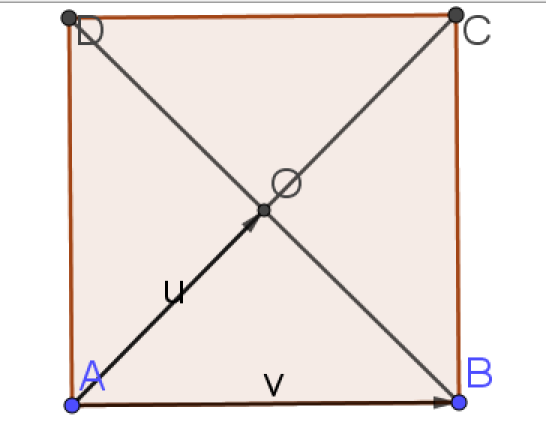
g. \(\vec{AB}\cdot\vec{AO}=AB \times AO \times cos(\frac{\pi}{4})=4 \times 2\sqrt{2}\times \frac{\sqrt{2}}{2}=4 \times \sqrt{2}^2=8\)
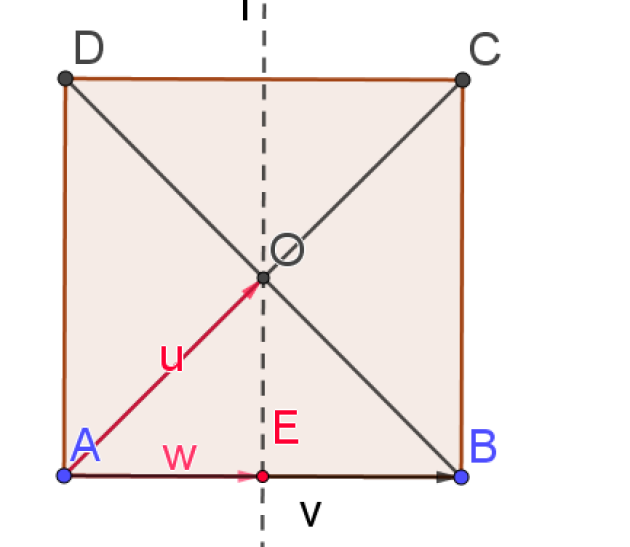
\(\vec{AB}\cdot\vec{AO}=AB \times AE=4 \times 2=8\)

\(\vec{AB}\cdot\vec{AO}=\vec{AO}\cdot\vec{AO}\) car B se projette orthogonalement en O sur (AO)
\(\vec{AB}\cdot\vec{AO}=AO \times AO=AO^2=(2\sqrt{2})^2=4 \times 2=8\)
Question
h. \(\vec{AB}\cdot\vec{CD}\)
Solution
h. \(\vec{AB}\cdot\vec{CD}=AB \times CD \times(\pi)=4 \times 4 \times (-1)=-16\)
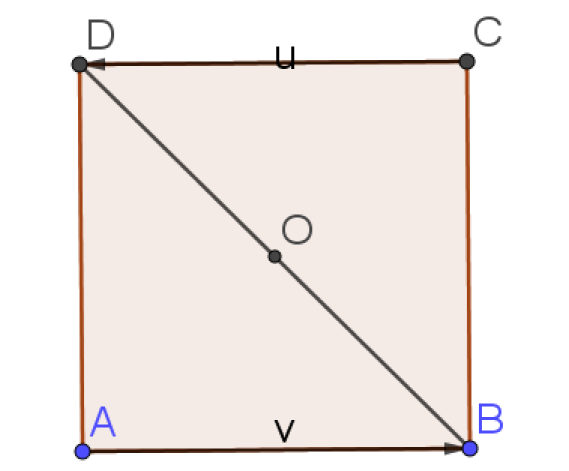
Question
i. \(\vec{AB}\cdot\vec{OD}\)
Solution
i. \(\vec{AB}\cdot\vec{OD}\)
\(\vec{AB}\cdot\vec{OD}=AB \times OD \times cos(135)=4 \times 2\sqrt{2} \times (\frac{-\sqrt{2}}{2})=-4(\sqrt{2})^2=-4 \times 2=-8\)
Question
j. \(\vec{AC}\cdot\vec{AD}\)\(\)
Solution
j. \(\vec{AC}\cdot\vec{AD}=AC \times AO=4\sqrt{2} \times 2\sqrt{2}=8(\sqrt{2})^2=8 \times 2=16\) car D se projette orthogonalement en O sur (AC)