Chapitre X Produit scalaire

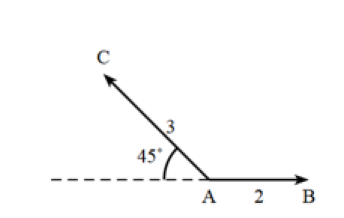
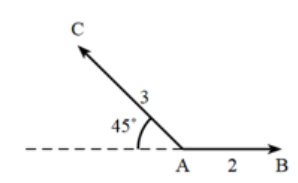
1.a.\(\vec{AB}\cdot\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})=AB \times AC \times cos(\widehat{BAC})\)

\(\vec{AB}\cdot\vec{AC}=2 \times 3 \times cos(180°-45°)\)

\(\vec{AB}\cdot\vec{AC}=6  \times cos(\pi-\frac{\pi}{4})\)

\(\vec{AB}\cdot\vec{AC}=6 \times cos(\frac{3\pi}{4})\)

\(\vec{AB}\cdot\vec{AC}=6 \times \frac{-\sqrt{2}}{2}\)

\(\vec{AB}\cdot\vec{AC}=-3\sqrt{2}\)

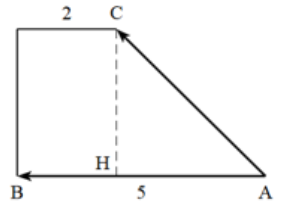
b.\(\vec{AB}\cdot\vec{AC}=AB \times AC \times cos(\vec{AB},\vec{AC})=AB \times AC \times cos(\widehat{BAC})=AC \times AH\)

en effet dans le triangle AHC rectangle en H

\(cos(\widehat{CAH})=cos(\widehat{CAB})=\frac{côté adjacent}{hypoténuse}=\frac{AH}{AC}\) donc \(AH=AC \times cos(\widehat{CAB})\)

or AH=5-2=3

finalement :

\(\vec{AB}\cdot\vec{AC}=5 \times 3=15\)

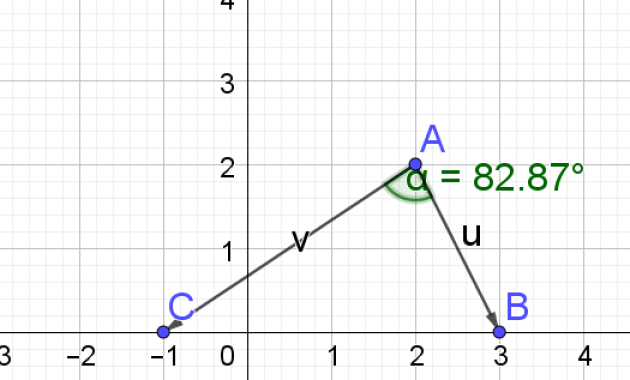
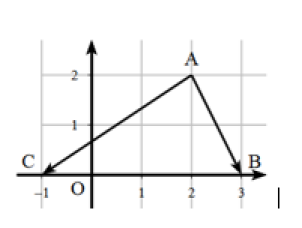
c.Dans le repère \((O,\vec{i},\vec{j})\) , les coordonnées des points sont :

A(2 ;2)

B(3 ;0)

C(-1 ;0)

donc \(\vec{AB}=\begin{pmatrix}3-2\\0-2\end{pmatrix}=\begin{pmatrix}1\\-2\end{pmatrix}\)

\(\vec{AC}=\begin{pmatrix}-1-2\\0-2\end{pmatrix}=\begin{pmatrix}-3\\-2\end{pmatrix}\)

\(\vec{AB}\cdot\vec{AC}=xx'+yy'=1\times (-3)+(-2)\times(-2)=-3+4=1\)

2. a.\( AB=\sqrt{x^2+y^2}=\sqrt{1^2+(-2)^2}=\sqrt{1+4}=\sqrt{5}\)

\(AC=\sqrt{x^2+y^2}=\sqrt{(-3)^2+(-2)^2}=\sqrt{9+4}=\sqrt{13}\)

\(b.\vec{AB}\cdot\vec{AC}=AB \times AC \times cos(\widehat{BAC})=1\)

\(\vec{AB}\cdot\vec{AC}=\sqrt{5} \times \sqrt{13} \times cos(\widehat{BAC})=1\)

\(\sqrt{65} cos(\widehat{BAC})=1\)

\(cos(\widehat{BAC})=\frac{1}{\sqrt{65}}\)

c.\(\widehat{BAC}=Arccos(\frac{1}{\sqrt{65}})\simeq 82,9°\)