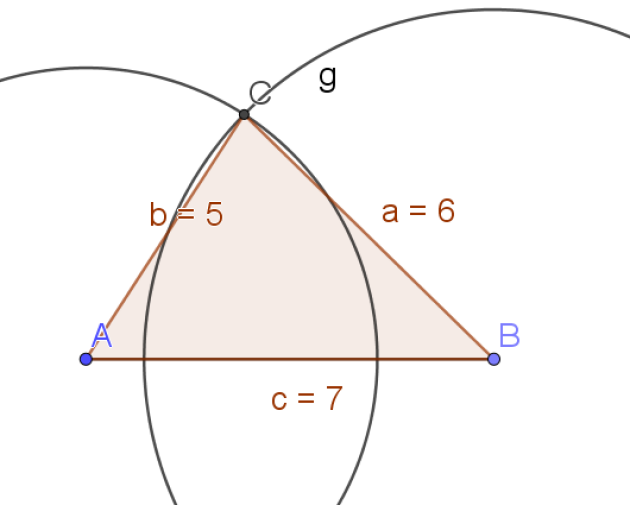
Exercice : Calcul d'angle 2
On considère un triangle ABC tel que AB=7 AC=5 et BC=6
Question
1. Donner la valeur du produit scalaire \(\vec{AB}.\vec{AC}\)
Solution
On utilise la formule d'Al-Kashi :
\(BC^2=AB^2+AC^2-2\vec{AB}\vec{AC}\)
\(6^2=7^2+5^2-2\vec{AB}\vec{AC}\)
\(36=49+25-2\vec{AB}\vec{AC}\)
\(36=74-2\vec{AB}\vec{AC}\)
\(36-74=-2\vec{AB}\vec{AC}\)
\(-38=-2\vec{AB}\vec{AC}\)
\(\vec{AB}\vec{AC}=19\)
Question
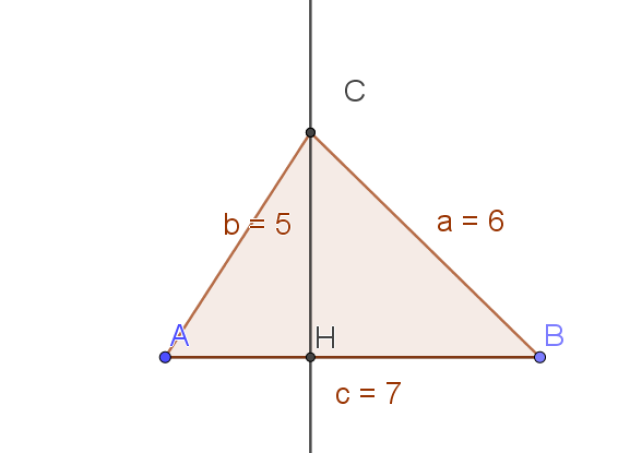
2.Soit H le projeté orthogonal de C sur (AB). Déterminer la longueur AH.\(\)
Solution
Soit H le projeté orthogonal de C sur (AB). Déterminer la longueur AH.
\(\vec{AB}\cdot\vec{AC}=\vec{AB}\cdot\vec{AH}\) car H est le projeté orthogonal de C sur (AB)
\(\vec{AB}\cdot\vec{AC}=AB \times AH = 7 \times AH\)
\(7 \times AH=19\)
\(AH=\frac{19}{7}\simeq2,7\)
Question
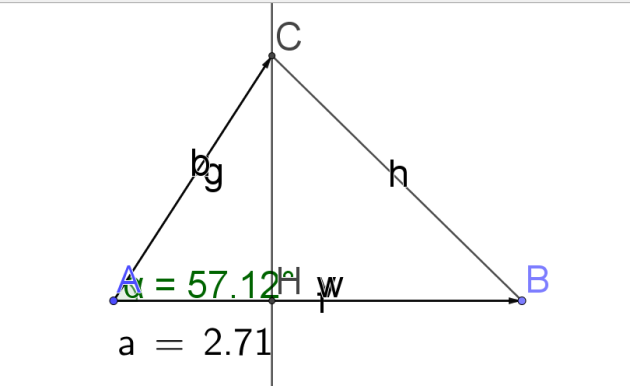
3.Déterminer une valeur approchée de la mesure en degré de l'angle \(\widehat{BAC}\)
Solution
\(\vec{AB}.\vec{AC}=AB \times AC \times cos(\widehat{BAC})=7 \times 5\times cos(\widehat{BAC})=35cos(\widehat{BAC})=19\)
\(cos(\widehat{BAC})=\frac{19}{35}\)
2.\(\widehat{BAC}=Arccos(\frac{19}{35})\)
3.\(\widehat{BAC}\simeq57,1°\)
