Exercice : Orthogonalité

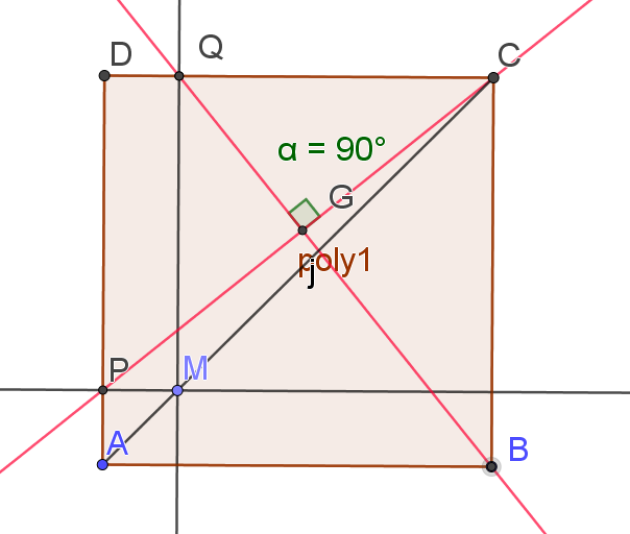
ABCD est un carré. M est un point du segment [AC] distinct de A et de C. P et Q sont les projetés orthogonaux de M respectivement sur [AD] et [DC] .

carre.ggb [ggb, 21,8 ko]

Question

1. Conjecturer la position relative des droites (BQ) et (CP).

Solution

Les droites (BQ) et (CP) semblent être perpendiculaires.

Question

2. On se place dans le repère \((A ;\vec{AB}.\vec{AD})\)

Donner les coordonnées des points B,Q,C et P en fonction des coordonnées du point M qu'on note \((x,y)\)

Solution

B(1,0), \(Q(x,1)\) ,C(1,1), \(P(0,y)\)

Question

3.Calculer le produit scalaire \(\vec{BQ}.\vec{CP}\). Valider la conjecture.

Solution

\(\vec{BQ}=\begin{pmatrix}x-1\\1-0\end{pmatrix}=\begin{pmatrix}x-1\\1\end{pmatrix}\)

\(\vec{CP}=\begin{pmatrix}0-1\\y-1\end{pmatrix}=\begin{pmatrix}-1\\y-1\end{pmatrix}\)

\(\vec{BQ}.\vec{CP}=(x-1) \times (-1) + 1 \times (y-1)=-x+1+y-1=y-x\)

or \(M \in (AC)\) donc \(y=x\)

donc \(\vec{BQ}.\vec{CP}=0\) les vecteurs \(\vec{BQ}\) et \(\vec{CP}\) sont donc orthogonaux

et les droites (BQ) et (CP) sont donc perpendiculaires.