Exercice : Formule d'Al Kashi
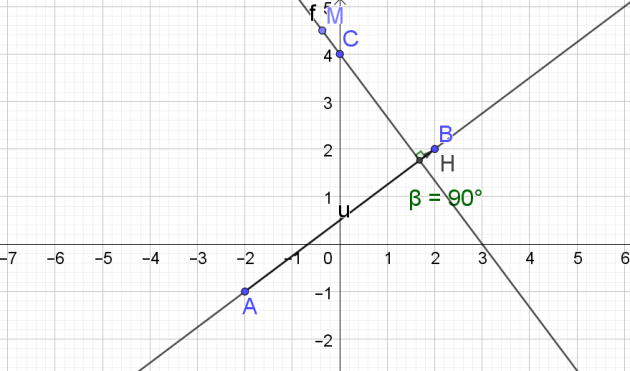
Le plan étant muni d'un repère orthonormé, on considère les points A\(\left(-2;-1\right)\),B\(\left(2;2\right)\) et \(C\left(0;4\right)\).
Question
1. Calculer les coordonnées des vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) puis le produit scalaire \(\overrightarrow{AB}\cdot\overrightarrow{AC}\).
Solution
\(\overrightarrow{AB}=\begin{pmatrix}2-(-2)\\2-(-1)\end{pmatrix}=\begin{pmatrix}4\\3\end{pmatrix}\)
\(\overrightarrow{AC}=\begin{pmatrix}0-(-2)\\4-(-1)\end{pmatrix}=\begin{pmatrix}2\\5\end{pmatrix}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=4 \times 2 + 3 \times 5=8+15=23\)
Question
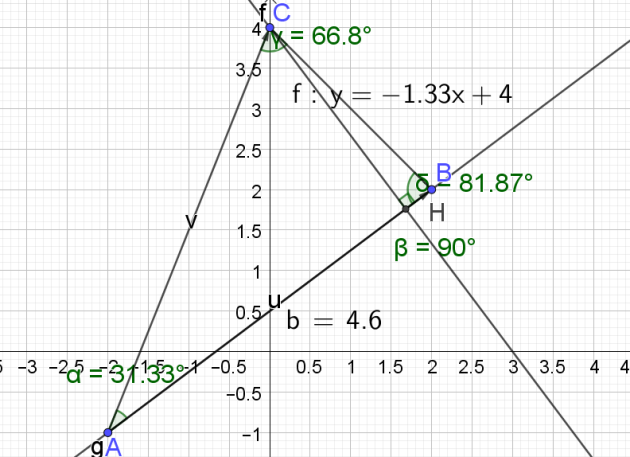
2. On appelle d la droite perpendiculaire à la droite \(\left(AB\right)\) passant par le point C. Déterminer l'équation réduite de la droite d.
Solution
Soit \(M(x,y)\) le point appartenant à la droite d perpendiculaire à la droite \(\left(AB\right)\) passant par le point C.
\(\overrightarrow{CM}=\begin{pmatrix}x-0\\y-4\end{pmatrix}=\begin{pmatrix}x\\y-4\end{pmatrix}\)
\(\overrightarrow{CM}\cdot\overrightarrow{AB}=\begin{pmatrix}x\\y-4\end{pmatrix} \cdot \begin{pmatrix}4\\3\end{pmatrix}=0\)
\(x \times 4 + (y-4) \times 3=0\)
\(4x+3y-12=0\)
\(3y=-4x+12\)
L'équation réduite de la droite (d) est donc \(y=\frac{-4}{3}x+4\)
Question
3. Montrer que la longueur du segment \(\left[AB\right]\) est 5.
Solution
\(AB=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\)
Question
4. Déduire des questions précédentes la longueur du segment \(\left[AH\right]\), H désignant le point d'intersection des droites d et \(\left(AB\right)\).
Solution
\(\overrightarrow{AB} \cdot \)\(\overrightarrow{AC}=\)\(\overrightarrow{AB} \cdot \)\(\overrightarrow{AH}=AB \times AH\)
donc \(AB \times AH=23\)
d'où 5 \(\times AH=23\)
\(AH=\frac{23}{5}=4,6\)
Question
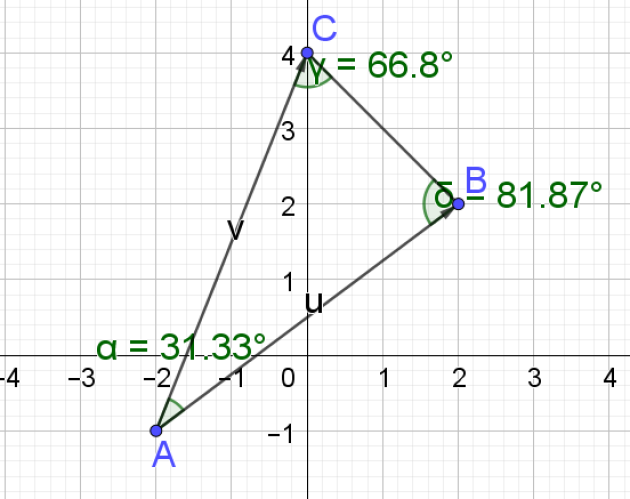
5. Déterminer les mesures des angles du triangle ABC
Solution
\(AC=\sqrt{2^2+5^2}=\sqrt{4+25}=\sqrt{29}\)
\(\vec{BC}=\begin{pmatrix}0-2\\4-2\end{pmatrix}\)\(=\begin{pmatrix}-2\\2\end{pmatrix}\)
\(BC=\sqrt{(-2)^2+2^2}=\sqrt{4+4}=\sqrt{8}\)
On utilise alors la Formule d'Al Kashi:
\(BC^2=AB^2+AC^2-2AB.AC.cos(\widehat{BAC})\)
\(8=25+29-2\times 5 \times \sqrt{29}.cos(\widehat{BAC})\)
\(8=54-2 \times 5 \times \sqrt{29}.cos(\widehat{BAC})\)
\(8-54=-10 \sqrt{29}.cos(\widehat{BAC})\)
\(-46=-10\sqrt{29}.cos(\widehat{BAC})\)
\(cos(\widehat{BAC})=\frac{46}{10\sqrt{29}}\)
\(\widehat{BAC}=Arccos(\frac{46}{10\sqrt{29}})\)
\(\widehat{BAC} \simeq 31,3°\)
\(AC^2=AB^2+BC^2-2AB.BC.cos(\widehat{ABC})\)
\(29=25+8-2\times 5 \times \sqrt{8}.cos(\widehat{ABC})\)
\(29=33-10 \times \sqrt{8}.cos(\widehat{ABC})\)
\(29-33=-10 \sqrt{8}.cos(\widehat{ABC})\)
\(-4=-10\sqrt{8}.cos(\widehat{ABC})\)
\(cos(\widehat{ABC})=\frac{4}{10\sqrt{8}}\)
\(\widehat{ABC}=Arccos(\frac{4}{10\sqrt{8}})\)
\(\widehat{BAC} \simeq 81,9°\)
\(AB^2=AC^2+BC^2-2AC.BC.cos(\widehat{ACB})\)
\(25=29+8-2\times sqrt{29} \times \sqrt{8}.cos(\widehat{ACB})\)
\(25=37-2\times sqrt{29} \times \sqrt{8}.cos(\widehat{ACB})\)
\(25-37=-2\times sqrt{29} \times \sqrt{8}.cos(\widehat{ACB})\)
\(-12=-2\times sqrt{29} \times \sqrt{8}.cos(\widehat{ACB})\)
\(cos(\widehat{ACB})=\frac{6}{\sqrt{29}\sqrt{8}}\)
\(\widehat{ACB}=Arccos(\frac{6}{\sqrt{29}\sqrt{8}})\)
\(\widehat{ACB} \simeq 81,9°\)