Exercice : Basique 1

L'objectif est de renforcer la capacité des élèves à étudier des problèmes

dont la résolution repose sur des calculs de distances et d'angles,

la démonstration d'alignement, de parallélisme ou d'orthogonalité.

Expression de deux vecteurs du plan en fonction de deux vecteurs non colinéaires

Capacités attendues : choisir une décomposition pertinente dans le cadre de la résolution de problèmes.

Commentaires : on ne se limite pas au cas de la géométrie repérée.

Produit scalaire

Capacités attendues :

- calculer le produit scalaire de deux vecteurs par différentes méthodes (projection orthogonale, analytiquement, à l'aide des normes et d'un angle, à l'aide des normes).

- choisir la méthode la plus adaptée en vue de la résolution d'un problème.

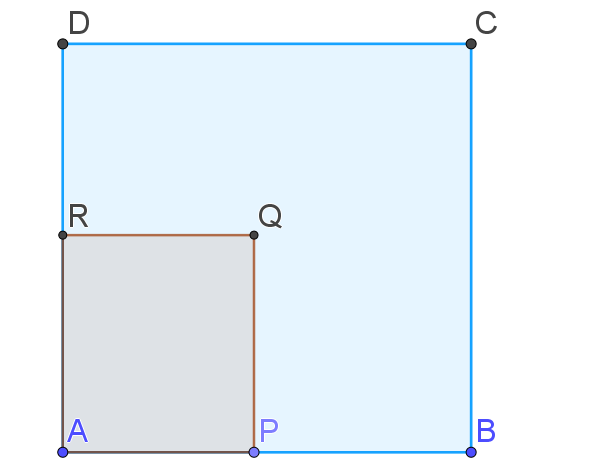
Soit ABCD un carré de sens direct.

On construit un rectangle APQR de sens direct tel que :

• P ∈ [AB] et R ∈ [AD] ;

• AP =DR.

Question

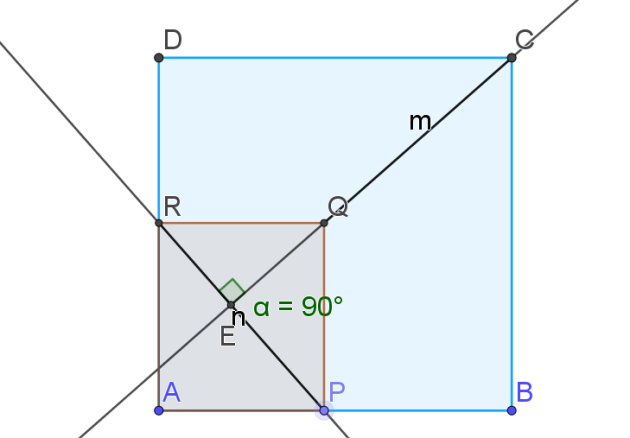
1.Que peut on conjecturer sur les droites (CQ) et (PR) ?

Solution

Carres.ggb [ggb, 17,2 ko]

Question

2. Justifier que \(\vec{CQ}.\vec{PR} =\vec{CQ}.(\vec{AR}-\vec{AP})\)

Solution

\(\vec{CQ}.\vec{PR} =\vec{CQ}.(\vec{PA}+\vec{AR})=\vec{CQ}.(-\vec{AP}+\vec{AR})\)\(=\vec{CQ}.(\vec{AR}-\vec{AP})\)

Question

3. En déduire que les droites (CQ) et (PR) sont perpendiculaires.

Solution

\(\vec{CQ}.\vec{PR} =\vec{CQ}.(\vec{AR}-\vec{AP})=\vec{CQ}.\vec{AR}-\vec{CQ}.\vec{AP}\)

\(\vec{CQ}.\vec{AR}=\vec{DR}.\vec{AR}=DR \times AR \times cos(\pi)=-DR \times AR\)

\(\vec{CQ}.\vec{AP}=\vec{BP}.\vec{AP}=BP \times AP \times cos(\pi)=-BP \times AP\)

or AP=DR et AR=BP

\(\vec{CQ}.\vec{AP}=-AR \times DR=\vec{CQ}.\vec{AP}\)

\(donc \vec{CQ}.\vec{AR}=\vec{CQ}.\vec{AP}\)

Finalement \(\vec{CQ}.\vec{PR}=0\)

et donc les droites (CQ) et (PR) sont perpendiculaires.