Exercice : Basique 13
Soit A ( – 1 ; 2 ) et B ( 5 ; 3 ) deux points du plan.
En utilisant le produit scalaire, déterminer les équations suivants :
Question
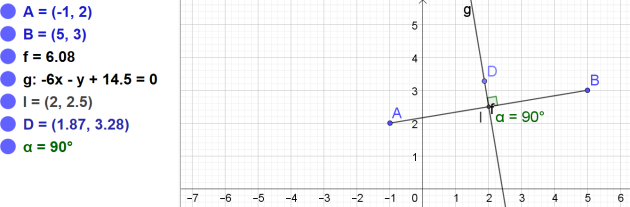
1. Equation affine de la droite \(\cal{D}\)' médiatrice du segment [AB].
Solution
Equation de la droite \(\cal{D}'\):
Soit M un point de la droite \(\cal{D}'\)
\(\vec{IM}.\vec{AB}=0\)
Coordonnées du point I milieu du segment [AB]:
\(x_I=\frac{x_A+x_B}{2}=\frac{-1+5}{2}=2\)
\(y_I=\frac{y_A+y_B}{2}=\frac{2+3}{2}=2,5\)
Coordonnées du vecteur \(\vec{AB}\)
\(\vec{AB}\)
\(=\begin{pmatrix}x_B-x_A\\y_B-y_A\end{pmatrix}\)
\(=\begin{pmatrix}5-(-1)\\3-2\end{pmatrix}\)
\(=\begin{pmatrix}5+1\\1\end{pmatrix}\)
\(=\begin{pmatrix}6\\1\end{pmatrix}\)
\(\vec{IM}.\vec{AB}=0\)
\(\iff \begin{pmatrix}x-2\\y-2,5\end{pmatrix}.\begin{pmatrix}6\\1\end{pmatrix}=0\)
\(\iff 6(x-2)+1(y-2,5)=0\)
\(\iff 6x-12+y-2,5=0\)
\(\iff 6x+y-14,5=0\)
L'équation affine de la droite \(\cal{D}\)' médiatrice du segment [AB] est donc \(6x+y-14,5=0\)
Question
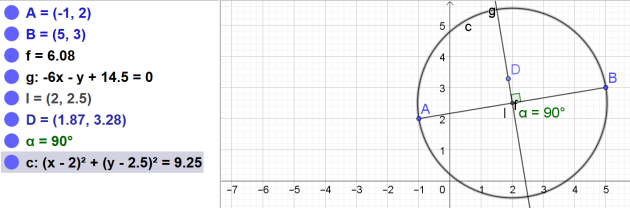
2. Equation de la forme \((x – a)² + (y – b)² = r²\) du cercle de diamètre [AB].
Solution
I est le centre du cercle donc :
\((x – 2)² + (y – 2,5)² = r²\)
\(r=\frac{AB}{2}\)
\(AB= \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(AB= \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(\vec{AB}=\begin{pmatrix}6\\1\end{pmatrix}\)
\(AB= \sqrt{6^2+1^2}=\sqrt{36+1}=\sqrt{37}\)
\(r=\frac{\sqrt{37}}{2}=\frac{\sqrt{37}}{\sqrt{4}}\)
\(\iff r=\sqrt{\frac{37}{4}}\)
\(\iff r=\sqrt{9,25}\)
\((x – 2)² + (y – 2,5)² = 9,25\)
L'équation du cercle de diamètre [AB] est \( (x – 2)² + (y – 2,5)² = 9,25\)
Question
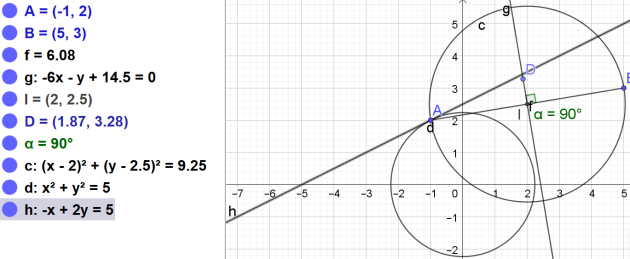
3. Equation cartésienne de la tangente en A au cercle de centre O et de rayon OA.
Solution
Soit M un point de la tangente au cercle de centre O et de rayon OA :
\(\vec{OA}.\vec{AM}=0\)
\(\iff \begin{pmatrix}x_A-0\\y_A-0\end{pmatrix}.\begin{pmatrix}x-x_A\\y-y_A\end{pmatrix}=0\)
\(\iff \begin{pmatrix}-1-0\\2-0\end{pmatrix}.\begin{pmatrix}x-(-1)\\y-2\end{pmatrix}=0\)
\(\iff \begin{pmatrix}-1\\2\end{pmatrix}.\begin{pmatrix}x+1\\y-2\end{pmatrix}=0\)
\(\iff -1(x+1)+2(y-2)=0\)
\(\iff -x-1+2y-4=0\)
\(\iff -x+2y-5=0\)
L'équation cartésienne de la tangente en A au cercle de centre O et de rayon OA a pour équation :
\(-x+2y-5=0\)