Exercice : Basique 8
ABC est un triangle rectangle en A.
H est le pied de la hauteur issue de A;
I est le milieu de [BC] ;
P et Q sont les projetés orthogonaux de H respectivement sur (AB) et (AC).
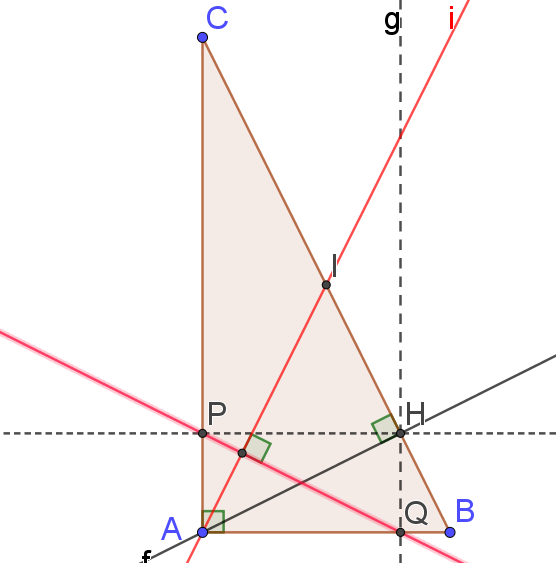
Question
1.Que peut on conjecturer pour les droites (AI) et (PQ) ?
Solution
On peut conjecturer que les droites (AI) et (PQ) sont orthogonales.
Question
2. Montrer que \(\frac{1}{2}\vec{AB} + \frac{1}{2}\vec{AC}=\vec{AI}\)
Solution
\(\frac{1}{2}\vec{AB} + \frac{1}{2}\vec{AC}\)
\(=\frac{1}{2}(\vec{AB} +\vec{AC})\)
Traçons la parallèle à la droite (AC) passant par le point B.
Traçons la parallèle à la droite (AB) passant par le point C.
Soit D leur point d'intersection.
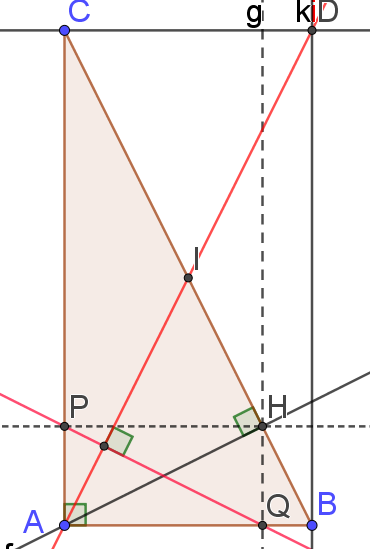
Le quadrilatère ABDC a ses côtés opposés parallèles
donc ABDC est un parallélogramme.
On a donc \(\vec{CD}=\vec{AB}\)
\(\frac{1}{2}\vec{AB} + \frac{1}{2}\vec{AC}\)
\(=\frac{1}{2}(\vec{CD} +\vec{AC})\)
\(=\frac{1}{2}(\vec{AC}+\vec{CD} )\)
\(=\frac{1}{2}\vec{AD}\)
or un parallélogramme a ses diagonales qui se coupent en leurs milieux.
I est donc le milieu de [AD]
donc \(\vec{AI}=\frac{1}{2}\vec{AD}\)
\(\iff \frac{1}{2}\vec{AB} + \frac{1}{2}\vec{AC}\)
\(=\frac{1}{2}\vec{AD}\)
\(=\vec{AI}\)
Remarque :
Le quadrilatère ABDC a un angle droit en A
donc ABDC est un rectangle.
2. Justifier que :
Question
a. \(\vec{AB}.\vec{PQ} =\vec{AB}.\vec{AH}\)
Solution
\(\vec{AB}.\vec{PQ} =\vec{AB}.\vec{AQ}=\vec{AB}.\vec{AH}\)
Question
b. \(\vec{AC}.\vec{PQ} =\vec{AC}.\vec{HA}\)
Solution
\(\vec{AC}.\vec{PQ} =\vec{AC}.\vec{PA}=\vec{AC}.\vec{HA}\)
Question
3. En déduire que \(\vec{AI}.\vec{PQ} = 0\).
Solution
\(\vec{AI}.\vec{PQ} = (\frac{1}{2}\vec{AB} + \frac{1}{2}\vec{AC}).\vec{PQ}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}\vec{AB}.\vec{PQ} + \frac{1}{2}\vec{AC}.\vec{PQ}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}\vec{AB}.\vec{AH} + \frac{1}{2}\vec{AC}.\vec{HA}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}\vec{AB}.\vec{AH} - \frac{1}{2}\vec{AC}.\vec{AH}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}(\vec{AB}.\vec{AH} - \vec{AC}.\vec{AH})\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}(\vec{AB} - \vec{AC}).\vec{AH}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}(\vec{AB} + \vec{CA}).\vec{AH}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2}( \vec{CA}+\vec{AB}).\vec{AH}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2} \vec{CB}.\vec{AH}\)
\(\iff \vec{AI}.\vec{PQ} = \frac{1}{2} \vec{CB}.\vec{AH}\)
or (CB) et (AH) sont orthogonales donc \(\vec{CB}.\vec{AH}=0\)
Finalement \(\vec{AI}\) et \(\vec{PQ}\) sont orthogonaux
et les droites (AI) et (PQ) sont donc perpendiculaires.