Exercice : Basique 3
ABCD est un carré.
M est un point du segment [AC] distinct de A et de C.
P et Q sont les projetés orthogonaux de M
respectivement sur [AD] et [DC].
Question
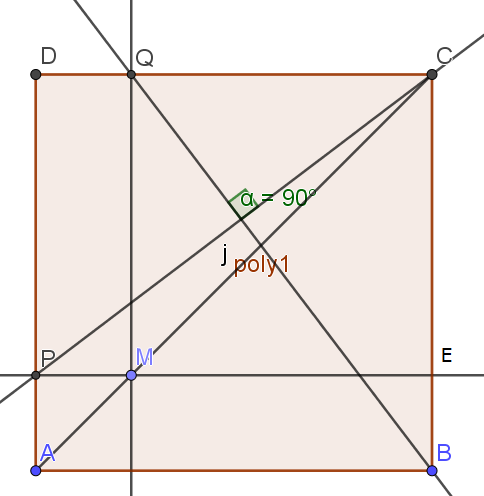
1. Conjecturer la position relative des droites (BQ) et (CP).
Solution
Les droites (BQ) et (CP) semblent être perpendiculaires.
Question
2. Calculer le produit scalaire \(\vec{BQ}.\vec{CP}\).
Indice
On décomposera le vecteur \(\vec{BQ}\) en introduisant le point C par la relation de Chasles.
On décomposera le vecteur \(\vec{CP}\) en introduisant le point D par la relation de Chasles.
Solution
\(\vec{BQ}.\vec{CP}\)
\(=(\vec{BC}+\vec{CQ}).(\vec{CD}+\vec{DP})\)
\(=\vec{BC}.\vec{CD}+\vec{BC}.\vec{DP}+\vec{CQ}.\vec{CD}+\vec{CQ}.\vec{DP}\)
\(\vec{BC}.\vec{CD}=0 \)car les vecteurs \(\vec{BC}\) et \(\vec{CD}\) sont orthogonaux.
\(\vec{BC}.\vec{DP}=- BC \times DP\)
car les vecteurs \(\vec{BC}\) et \(\vec{DP}\) ont même direction mais des sens contraires.
\(\vec{CQ}.\vec{CD}=CQ \times CD\)
car les vecteurs \(\vec{CQ}\) et \(\vec{CD}\) ont même direction et même sens.
\(\vec{CQ}.\vec{DP}=0 \)car les vecteurs \(\vec{CQ}\) et \(\vec{DP}\) sont orthogonaux.
\(\vec{BQ}.\vec{CP}=- BC \times DP+CQ \times CD\)
BC et CD sont des longueurs égales car ce sont les longueurs de deux côtés du carré ABCD
Montrons que les longueurs DP et CQ sont des longueurs égales.
Comme M se projette en P sur [DA] et en Q sur [DC]
(DP) et (QM) sont perpendiculaires à la même droite (DC)
donc (DP)//(QM)
(DQ) et (MP) sont perpendiculaires à la même droite (DA)
donc (DQ)//(MP)
Le quadrilatère DQMP est donc un parallélogramme.
De plus le quadrilatère DQMP possède un angle droit :
M se projette en P sur [DA]
donc DQMP est un rectangle.
Donc DP=QM
Comme M se projette en E sur [BC] et en Q sur [DC]
(ME) et (QC) sont perpendiculaires à la même droite (BC)
donc (ME)//(QC)
(MQ) et (EC) sont perpendiculaires à la même droite (DC)
donc (MQ)//(EC)
Le quadrilatère MECQ est donc un parallélogramme.
De plus M se trouve sur la bissectrice de l'angle \(\widehat{BCD}\)
or un point appartenant à la bissectrice est à égale distance
des deux côtés de l'angle
donc le parallélogramme MECQ possède deux côtés consécutifs égaux,
ME=MQ donc le parallélogramme MECQ est un losange.
De plus le losange MECQ possède un angle droit
car (MQ) est perpendiculaire à (CD)
donc le losange MECQ est donc un carré.
et CQ=QM
Finalement DP=QM=CQ
et
\(\vec{BQ}.\vec{CP}=- BC \times CQ+CQ \times BC=0\)
Les vecteurs \(\vec{BQ}\) et \(\vec{CP}\) sont donc orthogonaux.
Question
3. Valider la conjecture.
Solution
Les droites (BQ) et (CP) sont donc perpendiculaires.