Exercice : Basique 5
Le plan est muni d'un repère orthonormé et m un réel.
Soit \(\vec{u}=(16 ;m-6 )\) et \(\vec{v}=(m ;m+6)\)
Question
1. Déterminer les deux valeurs de m pour que \(\vec{u}\) et \(\vec{v}\) soient orthogonaux.
Solution
\(\vec{u}\) et \(\vec{v}\) sont orthogonaux.
donc \(\vec{u}.\vec{v}=0\)
\(\vec{u}=(16 ;m-6 )\) et \(\vec{v}=(m ;m+6)\)
\(16m+(m-6)(m+6)=0\)
\(\iff 16m+m^2-6^2=0\)
\(\iff m^2+16m-36=0\)
\(\Delta=b^2-4ac=16^2-4\times 1 \times (-36)\)
\(\iff \Delta=256+144=400\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-16-20}{2}\\x_2=\frac{-16+20}{2}\end{cases}\)
\(\iff \begin{cases}x_1=-18\\x_2=2\end{cases}\)
\(\vec{u}\) et \(\vec{v}\) sont orthogonaux pour m=-18 et m=2
Question
2. Calculer les coordonnées des deux vecteurs pour chacune de ces deux valeurs de m
Solution
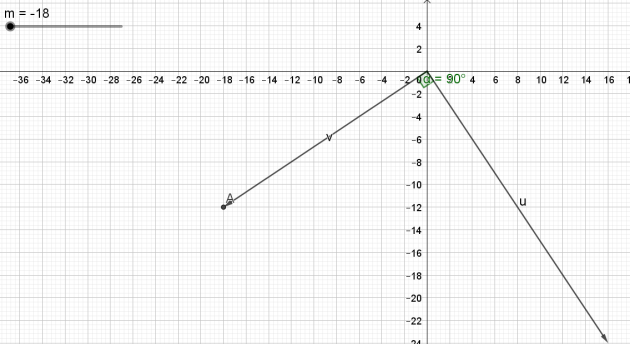
Pour m=-18 :
\(\vec{u}=(16 ;-18-6 )\) et \(\vec{v}=(-18 ;-18+6)\)
\(\vec{u}=(16 ;-24)\) et \(\vec{v}=(-18 ;-12)\)
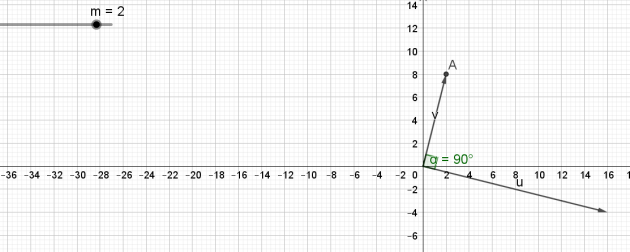
Pour m=2 :
\(\vec{u}=(16 ;2-6 )\) et \(\vec{v}=(2 ;2+6)\)
\(\vec{u}=(16 ;-4)\) et \(\vec{v}=(2;8)\)
Question
3. Faire un dessin dans ces deux cas. Vérifier géométriquement la propriété d'orthogonalité.