Exercice : Basique 14
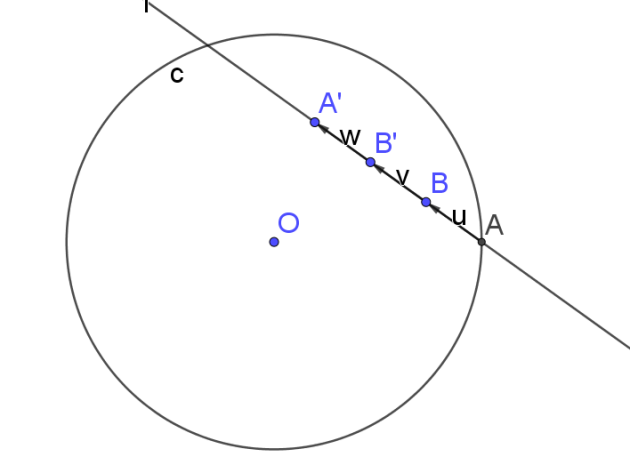
Soit O un point quelconque et \(\cal{C}\) le cercle de centre O et de rayon r.
A est un point de \(\cal{C}\) et d est une droite passant par A.
B est un point de cette droite et l'on défini le point A' tel que
\(\vec{AA'} = 3\vec{AB}\)
Question
1. Faire une figure.
Question
2. Construire en justifiant le cercle \(\cal{C}'\) image de \(\cal{C}\)
par l'homothétie h de centre B transformant A en A'.
(sans utiliser le rapport de l'homothétie).
Solution
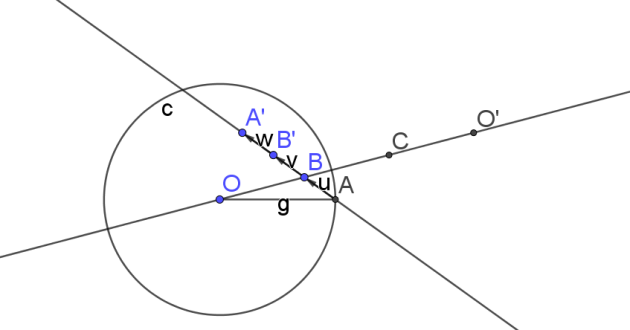
1.Construire l'image O'du centre O par l'homothétie h :
2. L'homothétie transforme le cercle \(\cal{C}\) en un cercle dont le centre est le point O'
(image du centre O par l'homothétie h)
et qui passe par l'ensemble des points images des points du cercle \(\cal{C}\)
donc comme A' est l'image du point A par l'homothétie h et que \(A\in \cal{C}\)
qui passe par A'
Question
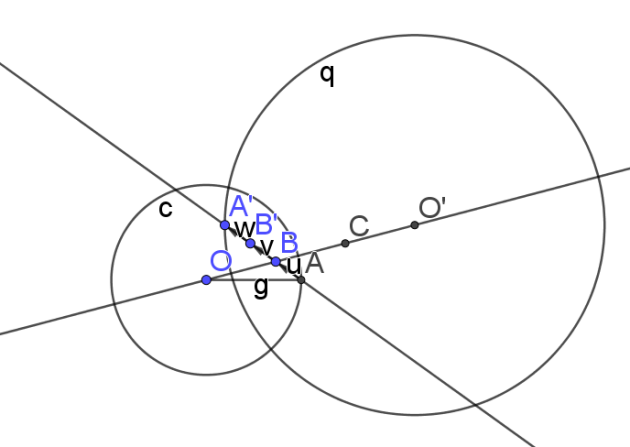
3. Déterminer le rapport de l'homothétie h puis préciser le rayon du cercle \(\cal{C}'\).
Dans le cas où r = 5.
Solution
Le rapport de l'homothétie est -2
\(\vec{AA'} = 3\vec{AB}\)
\(\iff \vec{AB}+\vec{BA'} = 3\vec{AB}\)
\(\iff \vec{BA'} = 3\vec{AB}-\vec{AB}\)
\(\iff \vec{BA'} = 2\vec{AB}\)
\(\iff \vec{BA'} = -2\vec{BA}\)
donc le rapport de l'homothétie est -2
et le rayon du nouveau cercle est donc 10