Exercice : Basique 15
Cet exercice est composé de deux parties indépendantes l'une de l'autre.
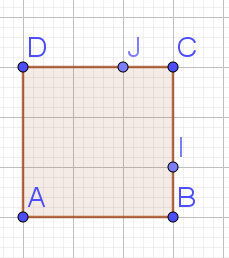
ABCD est un carré de côté 3.
I et J sont les points tels que :
\(\vec{BI} =\frac{1}{3}\vec{BC}\)
et
\(\vec{CJ}= \frac{1}{3}\vec{CD}\)
Partie A
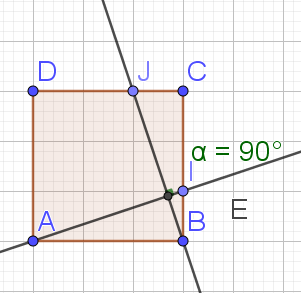
But de cette partie : montrer que les droites (AI) et (BJ) sont perpendiculaires.
Question
1. Calculer \(\vec{AI}.\vec{BJ}.\)
Indice
\(\vec{AI} =\vec{AB} +\vec{BI}\)
\(\vec{BJ}=\vec{BC} +\vec{CJ}\)
Solution
\(\vec{AI}.\vec{BJ} =(\vec{AB} +\vec{BI}).(\vec{BC} +\vec{CJ})\)
\(\vec{AI}.\vec{BJ} =\vec{AB}.\vec{BC}+\vec{AB}.\vec{CJ}+\vec{BI}.\vec{BC}+\vec{BI}.\vec{CJ}\)
\(\vec{AB}.\vec{BC}=0\) car les vecteurs \(\vec{AB}\) et \(\vec{BC}\) sont orthogonaux
\(\vec{AB}.\vec{CJ}=\vec{AB}.(\frac{1}{3}\vec{CD}\)
\(\iff \vec{AB}.\vec{CJ}=\frac{1}{3}\times \vec{AB} .\vec{CD}\)
\(\iff \vec{AB}.\vec{CJ}=\frac{1}{3}\times \vec{AB} .(-\vec{AB})\)
\(\iff \vec{AB}.\vec{CJ}=-\frac{1}{3}\times \vec{AB} .\vec{AB}\)
\(\iff \vec{AB}.\vec{CJ}=-\frac{1}{3}\times AB^2\)
\(\iff \vec{AB}.\vec{CJ}=-\frac{1}{3}\times 3^2\)
\(\iff \vec{AB}.\vec{CJ}=-\frac{1}{3}\times 9\)
\(\iff \vec{AB}.\vec{CJ}=-3\)
\(\vec{BI}.\vec{BC}=\frac{1}{3}\times \vec{BC} .\vec{BC}\)
\(\iff \vec{BI}.\vec{BC}=\frac{1}{3}\times BC^2\)
\(\iff \vec{BI}.\vec{BC}=\frac{1}{3}\times 3^2\)
\(\iff \vec{BI}.\vec{BC}=\frac{1}{3}\times 9\)
\(\iff \vec{BI}.\vec{BC}=3\)
\(\vec{BI}.\vec{CJ}=0\)
car les vecteurs \(\vec{BI}\) et \(\vec{CJ}\) sont orthogonaux
\(\vec{AI}.\vec{BJ}=0-3+3+0=0\)
Question
2. Conclure.
Solution
Comme
\(\vec{AI}.\vec{BJ}=0\)
Les vecteurs \(\vec{AI}\) et \(\vec{BJ}\) sont orthogonaux,
on en déduit que les droites (AI) et (BJ) sont perpendiculaires.
Partie B
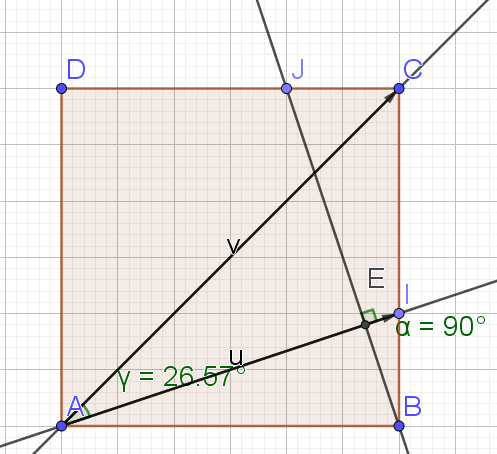
Le but de cette partie est de déterminer une mesure de l'angle \(\widehat{AIC}\).
Question
1.a. Calculer les longueurs AI et AC.
Solution
\(AI=\sqrt{1^2+3^2}=\sqrt{1+9}=\sqrt{10}\)
\(AC=\sqrt{3^2+3^2}=\sqrt{9+9}=\sqrt{18}=\sqrt{2\times 9}=3\sqrt{2}\)
Question
b. En déduire l'expression de \vec{AI}.\vec{AC} en fonction de cos((\vec{AI},\vec{AC}))
Solution
\(\vec{AI}.\vec{AC} = AI \times AC \times cos((\vec{AI},\vec{AC}))\)
\(\iff \vec{AI}.\vec{AC} = \sqrt{10} \times 3\sqrt{2} \times cos((\vec{AI},\vec{AC}))\)
\(\iff \vec{AI}.\vec{AC} = 3\sqrt{20} \times cos((\vec{AI},\vec{AC}))\)
\(\iff \vec{AI}.\vec{AC} = 3\sqrt{4 \times 5} \times cos((\vec{AI},\vec{AC}))\)
\(\iff \vec{AI}.\vec{AC} = 3 \times 2\sqrt{5} \times cos((\vec{AI},\vec{AC}))\)
\(\iff \vec{AI}.\vec{AC} = 6\sqrt{5} \times cos((\vec{AI},\vec{AC}))\)
2. On considère le repère \((A,\frac{\vec{AB}}{3} ,\frac{\vec{AD}}{3})\)
Question
a. Pourquoi ce repère est-il orthonormal ?
Solution
\(\vec{AB}\) et \(\vec{AD}\) sont orthogonaux car le quadrilatère est un carré.
Les normes \(||\frac{1}{3}\vec{AB}||\) et \(||\frac{1}{3}\vec{AD}||\) sont égales car le quadrilatère est un carré.
Question
b. Sans justifier, donner les coordonnées des points A,B,C,D,I et J.
Solution
A(0 ;0)
B(3 ;0)
C(3 ;3)
D(0 ;3)
I(3 ;1)
J(2 ;3)
Question
c. Calculer \(\vec{AI}.\vec{AC}\)
Solution
\(\vec{AI}=\left( \begin{array}{c} x_I-x_A\\y_I-y_A\end{array} \right )\)
\(\iff \vec{AI}=\left( \begin{array}{c} 3-0\\1-0\end{array} \right )\)
\(\iff \vec{AI}=\left( \begin{array}{c} 3\\1\end{array} \right )\)
\(\vec{AC}=\left( \begin{array}{c} x_C-x_A\\y_C-y_A\end{array} \right )\)
\(\iff \vec{AC}=\left( \begin{array}{c} 3-0\\3-0\end{array} \right )\)
\(\iff \vec{AC}=\left( \begin{array}{c} 3\\3\end{array} \right )\)
\(\vec{AI}.\vec{AC}=\left( \begin{array}{c} 3\\1\end{array} \right ) .\left( \begin{array}{c} 3\\3\end{array} \right )=9+3=12\)
Question
3. Déduire de ces deux questions une mesure approchée de l'angle
\((\vec{AI} ;\vec{AC}).\)
On arrondira au dixième.
Solution
\(\vec{AI}.\vec{AC} = 6\sqrt{5} \times cos((\vec{AI},\vec{AC}))=12\)
\(\iff cos((\vec{AI},\vec{AC}))=\frac{12}{6\sqrt{5}}\)
\(\iff cos((\vec{AI},\vec{AC}))=\frac{2}{\sqrt{5}}\)
\(\iff cos((\vec{AI},\vec{AC}))=\frac{2\sqrt{5}}{5}\)
\(\iff (\vec{AI},\vec{AC})=Arccos(\frac{2\sqrt{5}}{5})\simeq 26,6°\)