Exercice : Basique 6
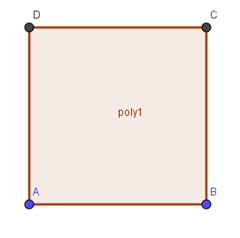
Soit ABCD un carré de côté 1.
Soit M le point de {AB] tel que
\(\vec{AM} =\frac{1}{3}\vec{AB}\)
et N le point de [BC] tel que \(\vec{BN}=\frac{1}{4}\vec{BC}\)
Question
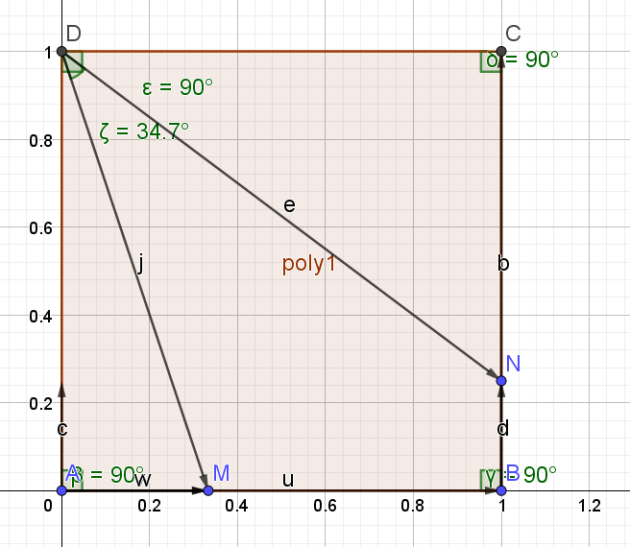
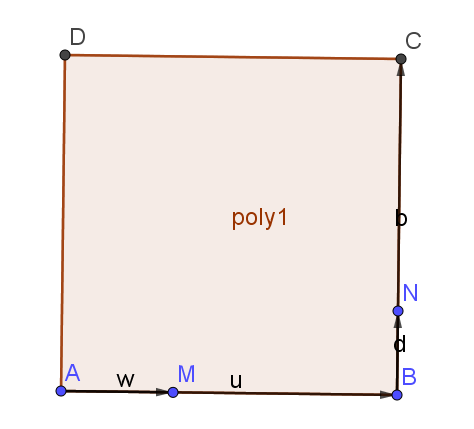
1.Faire une figure
Question
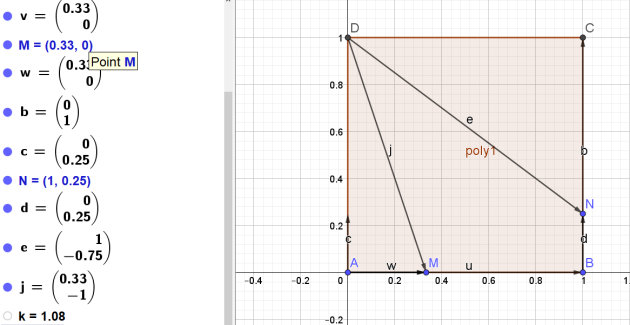
2.Déterminer les coordonnées des points D,M et N
dans le repère \((A,\vec{AB},\vec{AD})\)
Solution
D(0 ;1)
\(M(\frac{1}{3} ;0)\)
\(N(1 ;\frac{1}{4})\)
Question
3.En déduire le produit scalaire \(\vec{DM}.\vec{DN}\)
Indice
\(\vec{u}.\vec{v}=xx'+yy'\)
Solution
\(\vec{DM}=\left( \begin{array}{c}x_M-x_D\\y_M-y_D\end{array} \right )\)
\(\iff \vec{DM}=\left(\begin{array}{c}\frac{1}{3}-0\\0-1\end{array}\right)\)
\(\iff \vec{DM}=\left(\begin{array}{c}\frac{1}{3}\\-1\end{array}\right)\)
\(\vec{DN}=\left(\begin{array}{c}x_N-x_D\\y_N-y_D\end{array}\right)\)
\(\iff \vec{DM}=\left(\begin{array}{c}1-0\\\frac{1}{4}-1\end{array}\right)\)
\(\iff \vec{DM}=\left(\begin{array}{c}1\\-\frac{3}{4}\end{array}\right)\)
\(\vec{DM}.\vec{DN}\)
\(=\left(\begin{array}{c}\frac{1}{3}\\-1\end{array}\right).\left(\begin{array}{c}1\\-\frac{3}{4}\end{array}\right)\)
\(=\frac{1}{3} \times 1 +(-1) \times (-\frac{3}{4})\)
\(=\frac{1}{3} +\frac{3}{4}\)
\(=\frac{4}{12} +\frac{9}{12}\)
\(=\frac{13}{12}\)
Question
4.En utilisant le théorème de Pythagore dans des triangles rectangles à spécifier, déterminer les longueurs DM et DN
Solution
Dans le triangle DAM rectangle en A, d'hypoténuse [DM],
on utilise le théorème de Pythagore :
\(DM^2=DA^2+AM^2\)
\(\iff DM^2=1^2+(\frac{1}{3})^2\)
\(\iff DM^2=1+\frac{1}{9}\)
\(\iff DM^2=\frac{9}{9}+\frac{1}{9}\)
\(\iff DM^2=\frac{10}{9}\)
donc \(DM=\frac{\sqrt{10}}{3}\)
Dans le triangle DCN rectangle en C, d'hypoténuse [DN],
on utilise le théorème de Pythagore :
\(DN^2=DC^2+CN^2\)
\(\iff DN^2=1^2+(\frac{3}{4})^2\)
\(\iff DN^2=1+\frac{9}{16}\)
\(\iff DN^2=\frac{16}{16}+\frac{9}{16}\)
\(\iff DN^2=\frac{25}{16}\)
donc \(DN=\frac{5}{4}\)
Question
5.En écrivant que \(\vec{DM}.\vec{DN}=DM×DN×cos(\vec{DM} ;\vec{DN})\)
et en utilisant les questions précédentes
déterminer la valeur de \(cos(\vec{DM} ;\vec{DN} )\)
puis la mesure de l'angle de vecteurs \((\vec{DM} ;\vec{DN})\)
Solution
\vec{DM}.\vec{DN}=\frac{13}{12}
\(DM×DN×cos(\vec{DM} ;\vec{DN})=\frac{\sqrt{10}}{3}\times \frac{5}{4} \times cos(\vec{DM} ;\vec{DN})\)
donc
\(\frac{5\sqrt{10}}{12} \times cos(\vec{DM} ;\vec{DN})=\frac{13}{12}\)
\(cos(\vec{DM} ;\vec{DN})=\frac{\frac{13}{12}}{\frac{5\sqrt{10}}{12}}\)
\(cos(\vec{DM} ;\vec{DN})=\frac{13}{12} \times \frac{12}{5\sqrt{10}}\)
\(cos(\vec{DM} ;\vec{DN})=\frac{13}{5\sqrt{10}}\)
\((\vec{DM} ;\vec{DN})=Arccos(\frac{13}{5\sqrt{10}})\simeq34,7°\)