Exercice : Basique 11
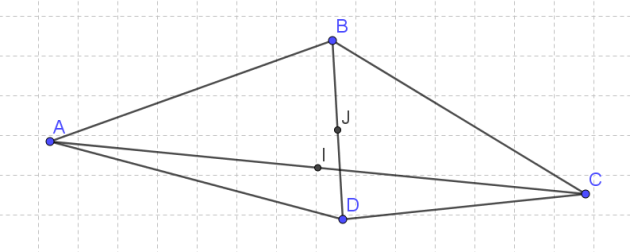
ABCD est un quadrilatère quelconque.
On appelle I et J les milieux respectifs des segments [AC] et [BD].
Question
1. Montrer que : \(AB^{2}+CB^{2}+CD^{2}+AD^{2}=4IJ^{2}+AC^{2}+BD^{2}\)
Solution
\(AB²=\vec{AB}^2=(\vec{AJ}+\vec{JB})^2\)
\(\iff AB²=\vec{AJ}^2+2\vec{AJ}.\vec{JB}+\vec{JB}^2\)
\(\iff AB²=AJ^2+2\vec{AJ}.\vec{JB}+BJ^2\)
\(AD²=\vec{AD}^2=(\vec{AJ}+\vec{JD})^2\)
\(\iff AD²=\vec{AJ}^2+2\vec{AJ}.\vec{JD}+\vec{JD}^2\)
\(\iff AD²=AJ^2+2\vec{AJ}.\vec{JD}+DJ^2\)
\(AB²+AD^2=AJ^2+2\vec{AJ}.\vec{JB}+BJ^2+AJ^2+2\vec{AJ}.\vec{JD}+DJ^2\)
\(\iff AB²+AD^2=2AJ^2+2\vec{AJ}.(\vec{JB}+\vec{JD})+BJ^2+DJ^2\)
Or J milieu de [BD] donc \(\vec{JB}=-\vec{JD}\) et \(BJ=DJ=\frac{BD}{2}\)
\(AB²+AD^2=2AJ^2+(\frac{BD}{2})^2+(\frac{BD}{2})^2\)
\(AB²+AD^2=2AJ^2+\frac{BD^2}{4}+\frac{BD^2}{4}\)
\(AB²+AD^2=2AJ^2+\frac{BD^2}{2}\)
\(CB²=\vec{CB}^2=(\vec{CJ}+\vec{JB})^2\)
\(\iff CB²=\vec{CJ}^2+2\vec{CJ}.\vec{JB}+\vec{JB}^2\)
\(\iff CB²=CJ^2+2\vec{CJ}.\vec{JB}+BJ^2\)
\(CD²=\vec{CD}^2=(\vec{CJ}+\vec{JD})^2\)
\(\iff CD²=\vec{CJ}^2+2\vec{CJ}.\vec{JD}+\vec{JD}^2\)
\(\iff CD²=CJ^2+2\vec{CJ}.\vec{JD}+DJ^2\)
\(CB²+CD^2=CJ^2+2\vec{CJ}.\vec{JB}+BJ^2+CJ^2+2\vec{CJ}.\vec{JD}+DJ^2\)
\(\iff CB²+CD^2=2CJ^2+2\vec{CJ}.(\vec{JB}+\vec{JD})+BJ^2+DJ^2\)
Or J milieu de [BD] donc \(\vec{JB}=-\vec{JD}\) et \(BJ=DJ=\frac{BD}{2}\)
\(CB²+CD^2=2CJ^2+(\frac{BD}{2})^2+(\frac{BD}{2})^2\)
\(CB²+CD^2=2CJ^2+\frac{BD^2}{4}+\frac{BD^2}{4}\)
\(CB²+CD^2=2CJ^2+\frac{BD^2}{2}\)
\(AB²+AD^2+CB²+CD^2=2CJ^2+\frac{BD^2}{2}+2AJ^2+\frac{BD^2}{2}\)
\(AB²+AD^2+CB²+CD^2=2CJ^2+2AJ^2+BD^2\)
\(AB²+AD^2+CB²+CD^2=2(AJ^2+CJ^2)+BD^2\)
\(AJ²=\vec{AJ}^2=(\vec{AI}+\vec{IJ})^2\)
\(\iff AJ²=\vec{AI}^2+2\vec{AI}.\vec{IJ}+\vec{IJ}^2\)
\(\iff AJ²=AI^2+2\vec{AI}.\vec{IJ}+IJ^2\)
\(CJ²=\vec{CJ}^2=(\vec{CI}+\vec{IJ})^2\)
\(\iff CJ²=\vec{CI}^2+2\vec{CI}.\vec{IJ}+\vec{IJ}^2\)
\(\iff CJ²=CI^2+2\vec{CI}.\vec{IJ}+IJ^2\)
\(AJ²+CJ²=AI^2+2\vec{AI}.\vec{IJ}+IJ^2+CI^2+2\vec{CI}.\vec{IJ}+IJ^2\)
\(AJ²+CJ²=AI^2+CI^2+2(\vec{AI}+\vec{CI}).\vec{IJ}+2IJ^2\)
Or I milieu de [AD] donc \(\vec{AI}=-\vec{CI}\) et \(AI=CI=\frac{AC}{2}\)
\(AJ²+CJ²=(\frac{AC}{2})^2+(\frac{AC}{2})^2+2IJ^2\)
\(AJ²+CJ²=\frac{AC^2}{4}+\frac{AC^2}{4}+2IJ^2\)
\(AJ²+CJ²=\frac{AC^2}{2}+2IJ^2\)
\(AB²+AD^2+CB²+CD^2=2(AJ^2+CJ^2)+BD^2\)
\(AB²+AD^2+CB²+CD^2=2(\frac{AC^2}{2}+2IJ^2)+BD^2\)
\(AB²+AD^2+CB²+CD^2=AC^2+4IJ^2+BD^2\)
\(AB²+AD^2+CB²+CD^2=4IJ^2+AC^2+BD^2\)
Question
2. Euler affirmait que ”la somme des carrés des côtés d'un quadrilatère est supérieure ou égale à la somme des carrés des diagonales”.
Peut-on avoir égalité ? Dans quel cas ?
Solution
\(AB²+AD^2+CB²+CD^2\) correspond à la somme des carrés des côtés du quadrilatère.
\(AC^2+BD^2\) correspond à la somme des carrés des diagonales du quadrilatère.
comme \(4IJ^2\ge0\)
\(AC^2+BD^2+4IJ^2\ge AC^2+BD^2\)
donc la propriété d'Euler est vérifiée.
Le cas d'égalité est obtenu pour \(4IJ^2=0\) soit pour IJ=0
donc le cas d'égalité est obtenu si les points I et J sont confondus.
Un quadrilatère a ses diagonales qui ont même milieu
si et seulement si les quadrilatère est un parallélogramme
donc ABCD est un parallélogramme : on retrouve l'égalité du parallélogramme.