Exercice : Basique 9
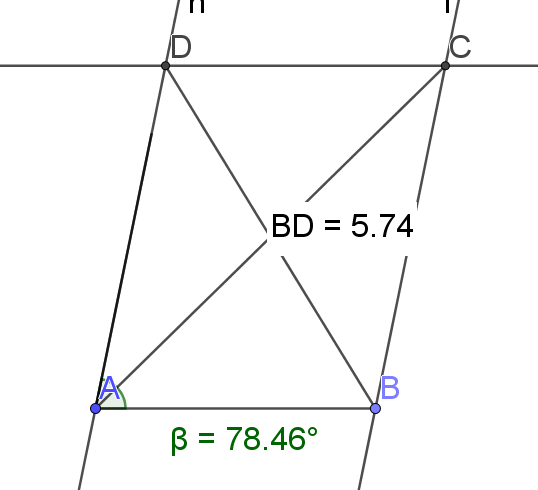
ABCD est un parallélogramme
avec AB = 4, AD = 5 et AC = 7.
Question
1.Calculer \(\vec{AB}.\vec{AD}\)
Solution
\((\vec{AB}+\vec{AD})^2=\vec{AB}^2+\vec{AB}.\vec{AD}+\vec{AD}^2\)
\(\iff (\vec{AB}+\vec{AD})^2=\vec{AB}^2+\vec{AB}.\vec{AD}+\vec{AD}^2\)
\(\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}\)
\(\iff \vec{AC}^2=\vec{AB}^2+2\vec{AB}.\vec{AD}+\vec{AD}^2\)
\(\iff 7^2=4^2+2\vec{AB}.\vec{AD}+5^2\)
\(\iff 49=16+2\vec{AB}.\vec{AD}+25\)
\(\iff 49=41+2\vec{AB}.\vec{AD}\)
\(\iff 8=2\vec{AB}.\vec{AD}\)
\(\iff \vec{AB}.\vec{AD}=4\)
\(\vec{AB}.\vec{AD}=4 \times 5 \times cos((\vec{AB},\vec{AD}))=4\)
\(\iff cos((\vec{AB},\vec{AD}))=\frac{4}{4 \times 5}\)
\(\iff cos((\vec{AB},\vec{AD}))=\frac{1}{5}\)
\(\iff cos((\vec{AB},\vec{AD}))=0,2\)
\(\iff (\vec{AB},\vec{AD})=Arccos(0,2)\simeq78,46\)
Question
2. En déduire BD
Solution
\(\vec{BD}^2=(\vec{BA}+\vec{AD})^2\)
\(\iff \vec{BD}^2=(-\vec{AB}+\vec{AD})^2\)
\(\iff \vec{BD}^2=(\vec{AD}-\vec{AB})^2\)
\(\iff \vec{BD}^2=\vec{AD}^2-2.\vec{AD}.\vec{AB}+\vec{AB}^2\)
\(\iff BD^2=AD^2-2.\vec{AD}.\vec{AB}+AB^2\)
\(\iff BD^2=AD^2-2.\vec{AD}.\vec{AB}+AB^2\)
\(\iff BD^2=5^2-2\times 4+4^2\)
\(\iff BD^2=25-8+16\)
\(\iff BD^2=41-8\)
\(\iff BD^2=33\)
\(\iff BD=\sqrt{33}\)