Exercice : Exercice 2024
Exercice 1
.
Question
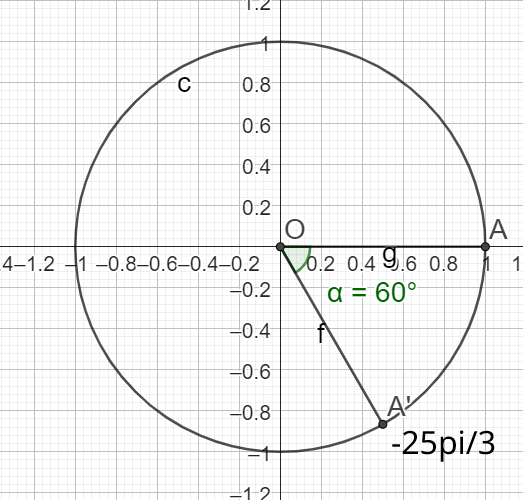
Donner la mesure principale des mesures \(\frac{-25\pi}{3}\) et \(2043\pi\)
Solution
\(\frac{\frac{-25\pi}{3}}{2\pi}=\frac{\frac{-25\pi}{3}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{-25\pi}{3}}{2\pi}=\frac{-25\pi}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-25\pi}{3}}{2\pi}=\frac{-25\pi}{6\pi}\)
or \(\frac{-30}{6}<\frac{-25}{6}<\frac{-24}{6}\)
\(\iff -5<\frac{-25}{6}<-4\)
donc \(\frac{-25\pi}{3}\) est compris entre -4 et -5 tours.
\(\frac{-25\pi}{3} + 4 \times 2 \pi\)
\(=\frac{-25\pi}{3} +8 \pi\)
\(=\frac{-25\pi}{3} +\frac{24 \pi}{3}\)
\(=-\frac{\pi}{3} \in ]-\pi ;\pi]\)
car \(]-\pi ;\pi]=]-\frac{3\pi}{3} ;\frac{3\pi}{3}]\)
La mesure principale de \(\frac{-25\pi}{3}\) est donc \(\frac{-\pi}{3}\)
(\(\frac{-25\pi}{3} + 5\times 2 \pi\)
\(=\frac{-25\pi}{3} +10 \pi\)
\(=\frac{-25\pi}{3} +\frac{30 \pi}{3}\)
\(=\frac{5\pi}{3} \notin ]-\pi ;\pi]\)
car \(]-\pi ;\pi]=]-\frac{3\pi}{3} ;\frac{3\pi}{3}]\))
\(\frac{2034\pi}{2\pi}=\frac{2043}{2}=1021,5\)
donc \(2043\pi\) est compris entre 1021 tours et 1022 tours.
\(2043\pi- 1021 \times 2 \pi\)
\(=2043 \pi - 2042 \pi\)
\(=\pi \in ]-\pi ;\pi]\)
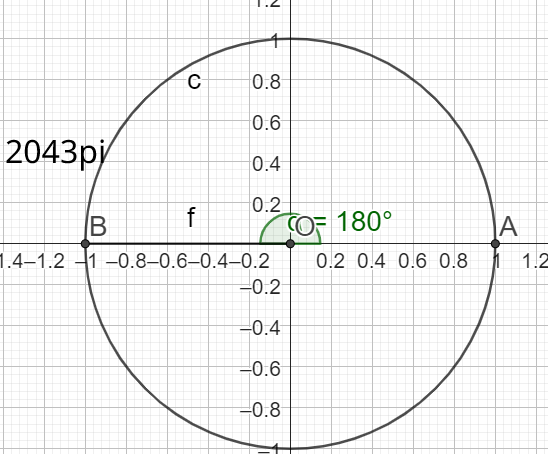
La mesure principale de \(2043\pi\) est donc \(\pi\)
(\(2043\pi- 1022 \times 2 \pi\)
\(=2043 \pi - 2044 \pi\)
\(=-\pi \notin ]-\pi ;\pi])\)
Exercice 2
Sachant que \(\cos(\frac{2\pi}{5})=\frac{\sqrt{5}-1}{4}\)
Question
1.Déterminer la valeur exacte de \(\cos(\frac{2\pi}{5})\)
Solution
\(cos (-x)=cos (x)\) pour tout \(x \in \mathbb{R}\)
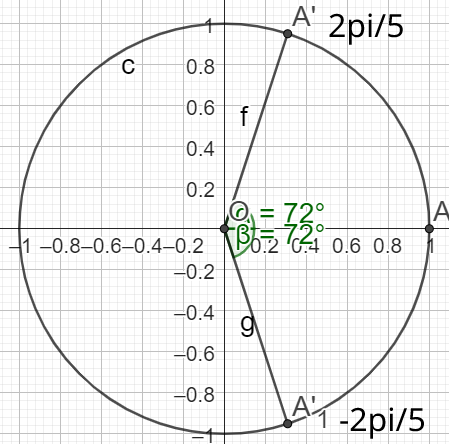
donc \(cos (-\frac{2\pi}{5})=cos (\frac{2\pi}{5})=\frac{\sqrt{5}-1}{4}\)
Question
2. Déterminer la valeur exacte de \(sin (\frac{2\pi}{5})\) et \(sin (\frac{3\pi}{5})\)
Solution
\(\cos^2(x)+\sin^2(x)=1\) pour tout \(x \in \mathbb{R}\)
donc \(\cos^2(\frac{2\pi}{5})+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left ( \frac{\sqrt{5}-1}{4} \right )^2+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{\sqrt{5}^2-2\times \sqrt{5} \times 1+ 1^2}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left (\frac{5-2\sqrt{5}+1}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left (\frac{6-2\sqrt{5}}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \sin^2(\frac{2\pi}{5})=1-\left (\frac{6-2\sqrt{5}}{16} \right )\)
\(\iff \sin^2(\frac{2\pi}{5})=\frac{16}{16}-\left (\frac{6-2\sqrt{5}}{16} \right )\)
\(\iff \sin^2(\frac{2\pi}{5})=\frac{10+2\sqrt{5}}{16}\)
\(\iff \sin(\frac{2\pi}{5})=\frac{\sqrt{10+2\sqrt{5}}}{4}\) ou \(\sin(\frac{2\pi}{5})=-\frac{\sqrt{10+2\sqrt{5}}}{4}\)
or \(\frac{2\pi}{5}=\frac{4\pi}{10} \in [0 ;\frac{\pi}{2}]=[0 ;\frac{5\pi}{10}]\)
donc \(\sin(\frac{2\pi}{5})=\frac{\sqrt{10+2\sqrt{5}}}{4}\)
\(sin (\pi-x)=sin(x)\) pour tout \(x \in \mathbb{R}\)
donc \(sin (\pi-\frac{2\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{5\pi}{5}-\frac{2\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{3\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{3\pi}{5})= \frac{\sqrt{10+2\sqrt{5}}}{4}\)
Question
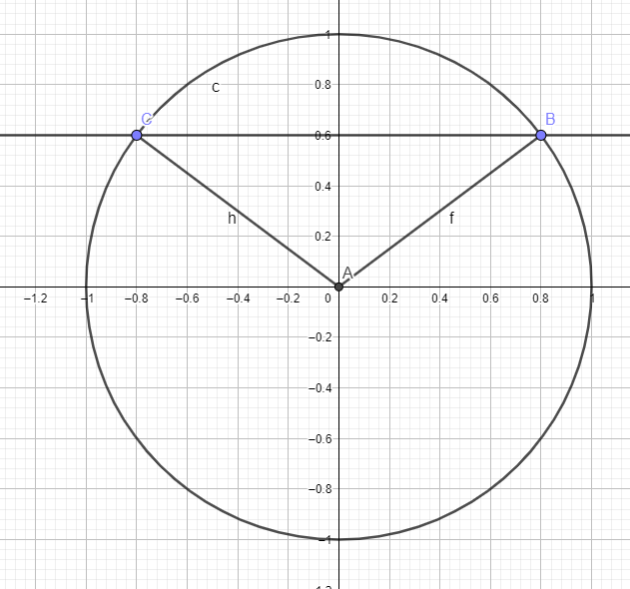
3.A l'aide du cercle trigonométrique, en déduire les valeurs de \(cos(\frac{3\pi}{5})\) et \(sin(\frac{\pi}{10})\)
Solution
\(cos (\pi-x)=-cos(x)\) pour tout \(x \in \mathbb{R}\)
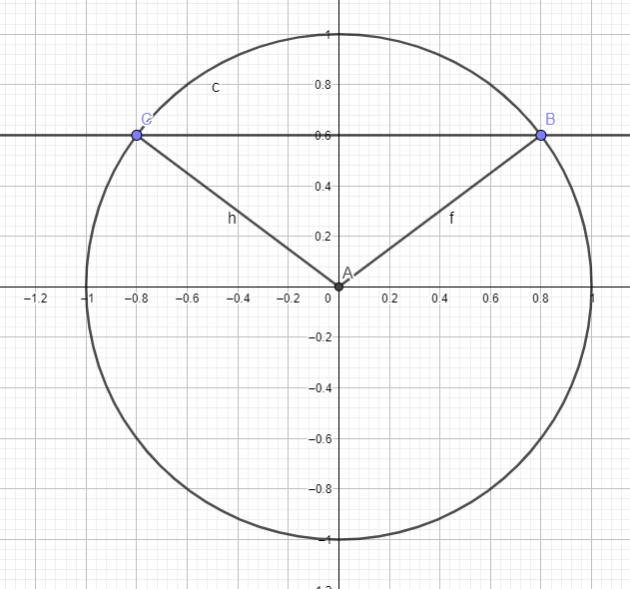
donc \(\cos (\pi-\frac{2\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{5\pi}{5}-\frac{2\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{3\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{3\pi}{5})= -\frac{\sqrt{5}-1}{4}\)
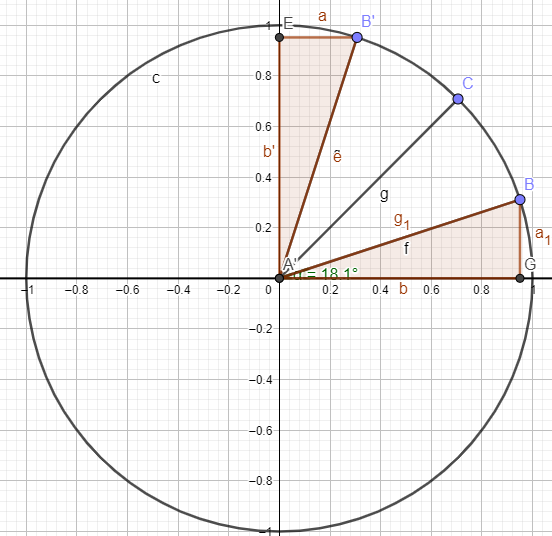
\(\sin(\frac{\pi}{2}-x)=\cos(x)\)
\(\sin(\frac{\pi}{2}-\frac{2\pi}{5})=\cos(\frac{2\pi}{5})\)
\(\iff \sin(\frac{5\pi}{10}-\frac{4\pi}{10})=\frac{\sqrt{5}-1}{4}\)
\(\iff \sin(\frac{\pi}{10})=\frac{\sqrt{5}-1}{4}\)
Exercice 3
Ecrire le plus simplement possible. Expliquer brièvement mais soigneusement chacune des égalités
Question
1.\(sin(\frac{\pi}{9})-sin(\frac{7\pi}{9})+sin(\frac{2\pi}{9})+sin(\frac{10\pi}{9})\)
Solution
\(sin(\frac{10\pi}{9})=-sin(\frac{\pi}{9})\)
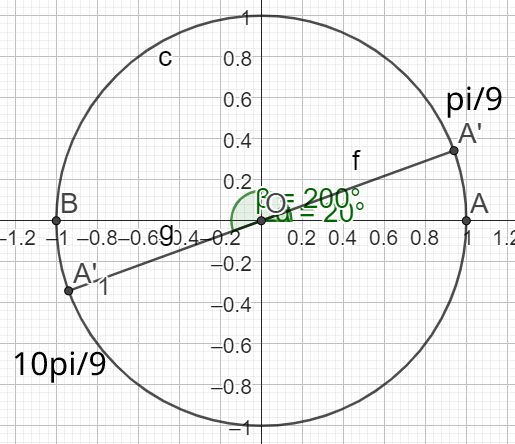
\(sin(\frac{7\pi}{9})=sin(\frac{2\pi}{9})\)
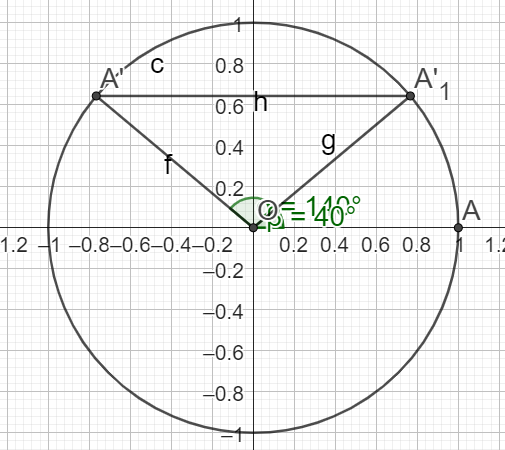
Finalement
\(sin(\frac{\pi}{9})-sin(\frac{7\pi}{9})+sin(\frac{2\pi}{9})+sin(\frac{10\pi}{9})\)
\(=sin(\frac{\pi}{9})-sin(\frac{2\pi}{9})+sin(\frac{2\pi}{9})+sin(\frac{\pi}{9})\)
\(=0\)
Question
2.\(sin(\frac{\pi}{2}-x)+cos(x+2\pi)+sin(x+3\pi)+sin(x+2\pi)+cos(\frac{\pi}{2}+x)\)
Solution
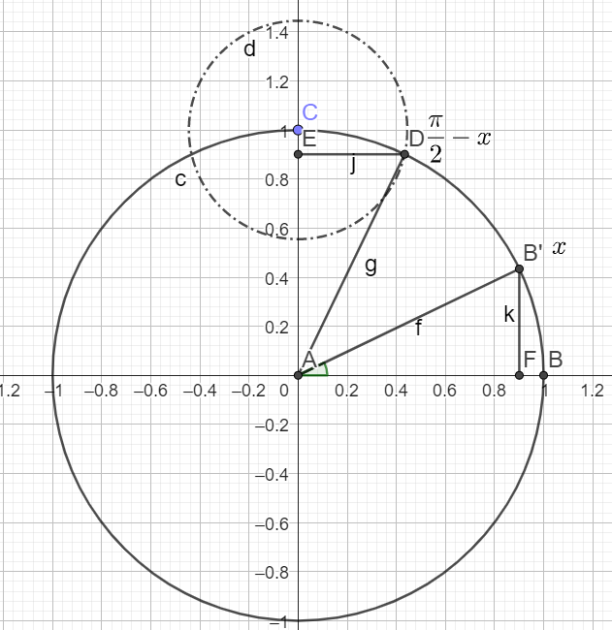
\(sin(\frac{\pi}{2}-x)=cos(x)\)
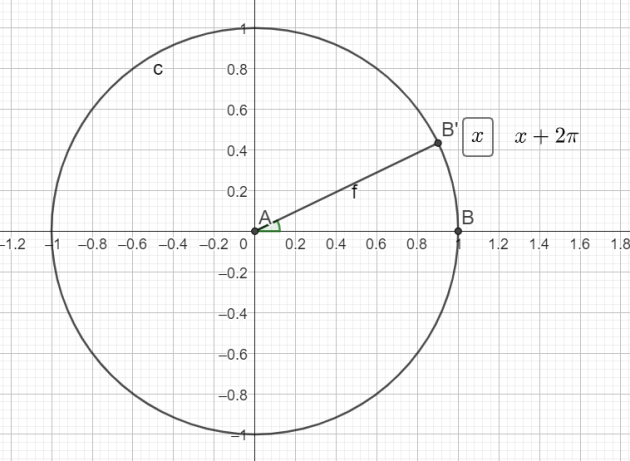
\(cos(x+2\pi)=cos(x)\)
\(sin(x+2\pi)=sin(x)\)
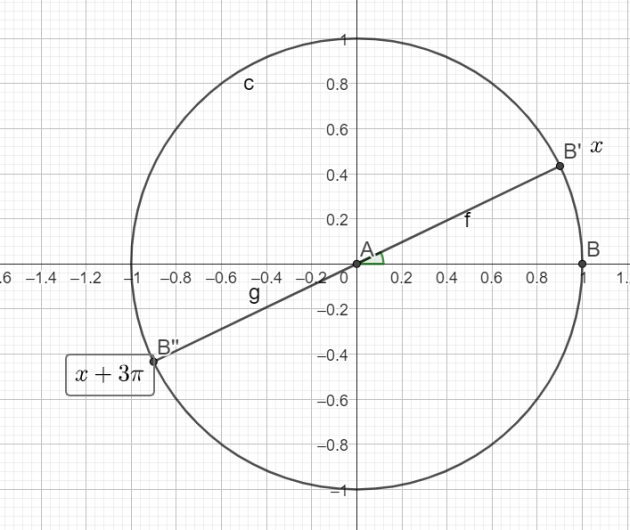
\(sin(x+3\pi)=-sin(x)\)
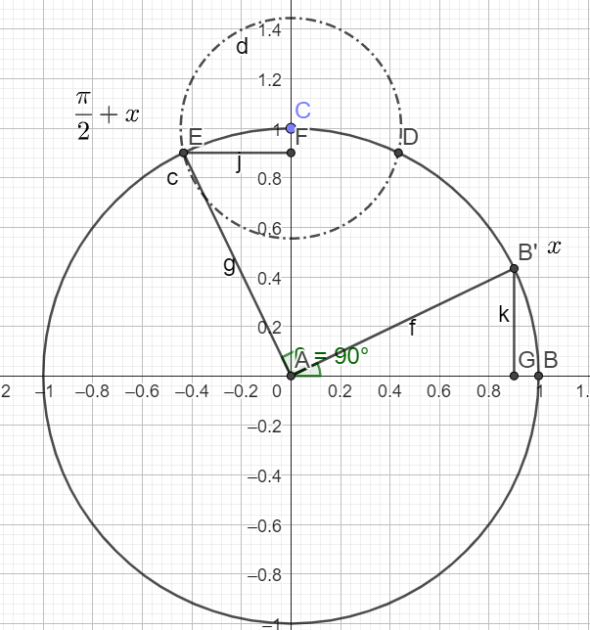
\(cos(\frac{\pi}{2}+x)=-sin(x)\)
\(sin(\frac{\pi}{2}-x)+cos(x+2\pi)+sin(x+3\pi)+sin(x+2\pi)+cos(\frac{\pi}{2}+x)\)
\(=cos(x)+cos(x)-sin(x)+sin(x)-sin(x)\)
\(=2cos(x)-sin(x)\)
Question
3.\(sin(0)+sin(\frac{\pi}{3})+sin(\frac{2\pi}{3})+sin(\pi)+sin(\frac{4\pi}{3})+sin(\frac{5\pi}{3})+sin(2\pi)\)
Solution
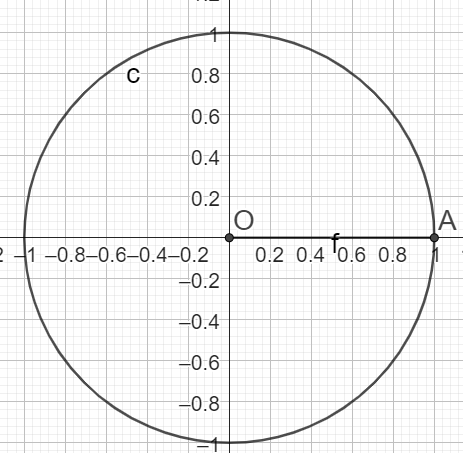
\(sin(0)=sin(2\pi)=0\)
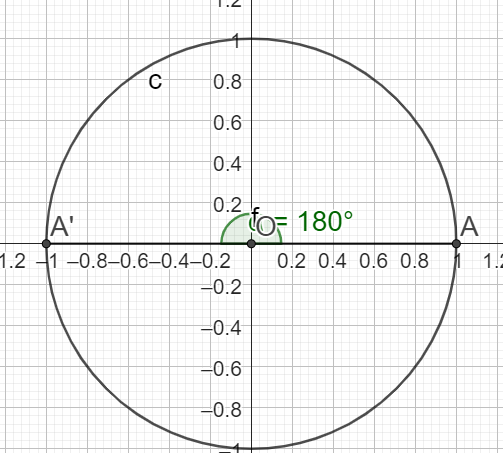
\(sin(\pi)=0\)
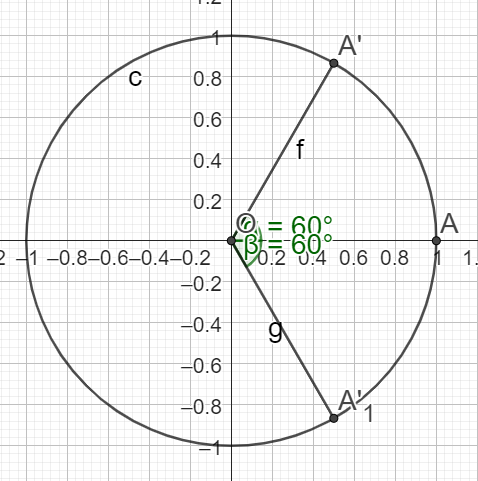
\(sin(\frac{5\pi}{3})=-sin(\frac{\pi}{3})\)
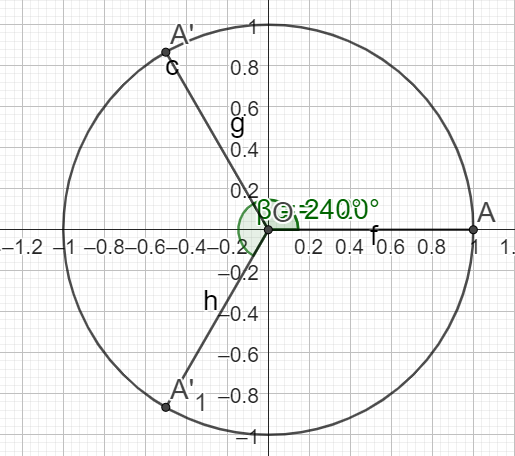
\(sin(\frac{4\pi}{3})=-sin(\frac{2\pi}{3})\)
\(sin(0)+sin(\frac{\pi}{3})+sin(\frac{2\pi}{3})+sin(\pi)+sin(\frac{4\pi}{3})+sin(\frac{5\pi}{3})+sin(2\pi)\)
\(=0+sin(\frac{\pi}{3})+sin(\frac{2\pi}{3})+0-sin(\frac{2\pi}{3})-sin(\frac{\pi}{3})+0\)
\(=0\)
Exercice 4
Résoudre les équations et inéquations suivantes,
on fera apparaître les images des solutions sur le cercle trigonométrique.
Question
1.\(2cos(x)-1=0\) sur \(I=\mathbb{R}\)
Solution
\(2cos(x)-1=0\)
\(\iff 2cos(x)=1\)
\(\iff cos(x)=\frac{1}{2}\)
\(\iff S=\{\frac{\pi}{3}+2k\pi ;\frac{-\pi}{3}+2k\pi\}\) pour \(k \in \mathbb{Z}\)
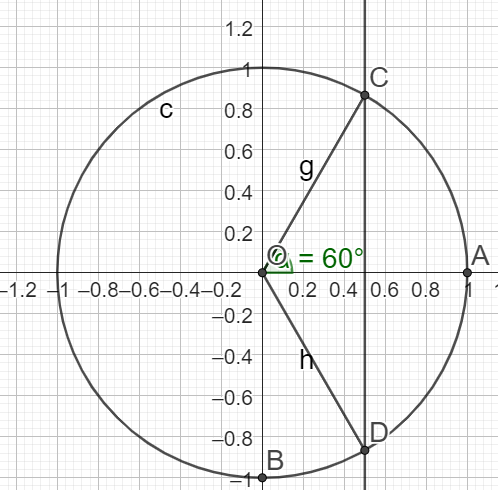
Question
2.\((2sin(x)-\sqrt{3})(\sqrt{2}cos(x)+1)=0\) sur \(I=\mathbb{R}\) puis sur \(J=]-\pi ;\pi]\)
Solution
\((2sin(x)-\sqrt{3})(\sqrt{2}cos(x)+1)=0\)
On utilise le théorème du produit nul :
\(\color{red}{\text{Théorème du produit nul :}}\)
\(\color{red}{\text{Un produit de facteurs est nul}}\)
\(\color{red}{\text{si et seulement si }}\)
\(\color{red}{\text{un de facteurs au moins est nul. }}\)
\(\iff 2sin(x)-\sqrt{3}=0\) ou \(\sqrt{2}cos(x)+1=0\)
\(\iff 2sin(x)=\sqrt{3}\) ou \(\sqrt{2}cos(x)=-1\)
\(\iff sin(x)=\frac{\sqrt{3}}{2}\) ou \(cos(x)=-\frac{1}{\sqrt{2}}\)
\(\iff sin(x)=\frac{\sqrt{3}}{2}\) ou \(cos(x)=-\frac{\sqrt{2}}{\sqrt{2}^2}\)
\(\iff sin(x)=\frac{\sqrt{3}}{2}\) ou \(cos(x)=-\frac{\sqrt{2}}{2}\)
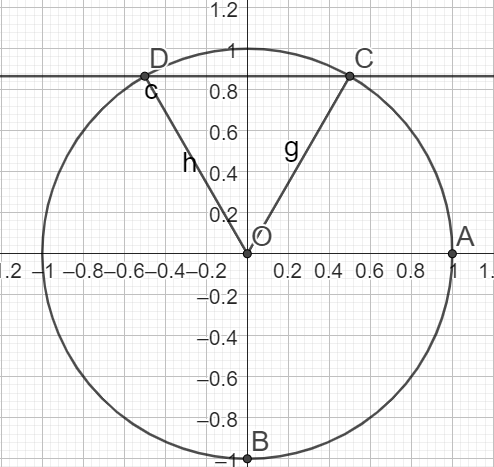
\(sin(x)=\frac{\sqrt{3}}{2}\)
\(\iff x \in \{\frac{\pi}{3}+2k\pi ;\pi -\frac{\pi}{3}+2k\pi \}\) \(k \in \mathbb{Z}\)
\(\iff x \in \{\frac{\pi}{3}+2k\pi ;\frac{3\pi}{3} -\frac{\pi}{3}+2k\pi \}\) \(k \in \mathbb{Z}\)
\(\iff x \in \{\frac{\pi}{3}+2k\pi ;\frac{2\pi}{3}+2k\pi \}\) \(k \in \mathbb{Z}\)
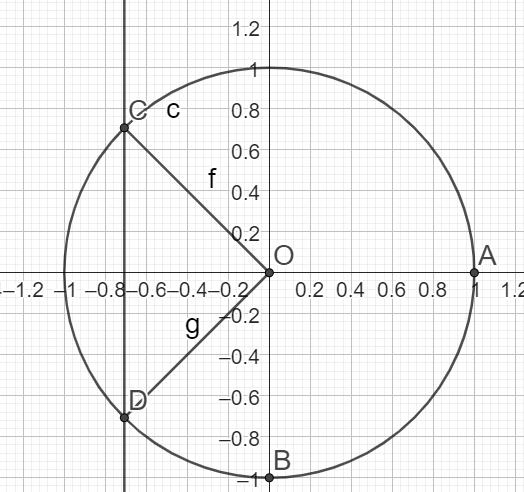
\(cos(x)=-\frac{\sqrt{2}}{2}\)
\(\iff x \in \{\frac{\pi}{2}+\frac{\pi}{4}+2k\pi ;-\frac{\pi}{2}-\frac{\pi}{4}+2k\pi \}\) \(k \in \mathbb{Z}\)
\(\iff x \in \{\frac{2\pi}{4}+\frac{\pi}{4}+2k\pi ;-\frac{2\pi}{4}-\frac{\pi}{4}+2k\pi \}\) \(k \in \mathbb{Z}\)
\(\iff x \in \{\frac{3\pi}{4}+2k\pi ;-\frac{3\pi}{4}+2k\pi \}\) \(k \in \mathbb{Z}\)
Sur I, les solutions sont
\(S=\{-\frac{3\pi}{4}+2k\pi ; \frac{\pi}{3}+2k\pi;\frac{2\pi}{3}+2k\pi;\frac{3\pi}{4}+2k\pi \}\) \(k \in \mathbb{Z}\)
Sur J, les solutions sont \(S=\{-\frac{3\pi}{4} ; \frac{\pi}{3};\frac{2\pi}{3};\frac{3\pi}{4} \}\)
Question
3.\(4cos^2(x)+2(\sqrt{3}-1)cos(x)-\sqrt{3}=0\) sur \(I=\mathbb{R}\) puis sur \(J=]-2\pi ;2\pi]\)
Solution
On pose \(X=cos(x)\)
\(\Rightarrow 4X^2+2(\sqrt{3}-1)X-\sqrt{3}=0\)
\(a=4\) \(b=2(\sqrt{3}-1)\) \(c=-\sqrt{3}\)
\(\Delta=b^2-4ac=(2(\sqrt{3}-1))^2-4 \times 4 \times (-\sqrt{3})\)
\(\iff \Delta=4(\sqrt{3}-1)^2+16\sqrt{3}\)
\(\iff \Delta=4(\sqrt{3}^2-2\sqrt{3}+1)+16\sqrt{3}\)
\(\iff \Delta=4(3-2\sqrt{3}+1)+16\sqrt{3}\)
\(\iff \Delta=4(3-2\sqrt{3}+1+4\sqrt{3})\)
\(\iff \Delta=4(3+2\sqrt{3}+1)\)
\(\iff \Delta=4(\sqrt{3}+1)^2\)
\(\iff \sqrt{\Delta}=2(\sqrt{3}+1)\)
Comme \(\Delta>0\), l'équation \(4X^2+2(\sqrt{3}-1)X-\sqrt{3}=0\)
admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2(\sqrt{3}-1)-2(\sqrt{3}+1)}{2 \times 4}\\X_2=\frac{-2(\sqrt{3}-1)+2(\sqrt{3}+1)}{2 \times 4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2\sqrt{3}+2-2\sqrt{3}-2}{8}\\X_2=\frac{-2\sqrt{3}+2+2\sqrt{3}+2}{8}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-4\sqrt{3}}{8}\\X_2=\frac{4}{8}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-\sqrt{3}}{2}\\X_2=\frac{1}{2}\end{cases}\)
\(\Rightarrow \begin{cases}cos(x_1)=\frac{-\sqrt{3}}{2}\\cos(x_2)=\frac{1}{2}\end{cases}\)
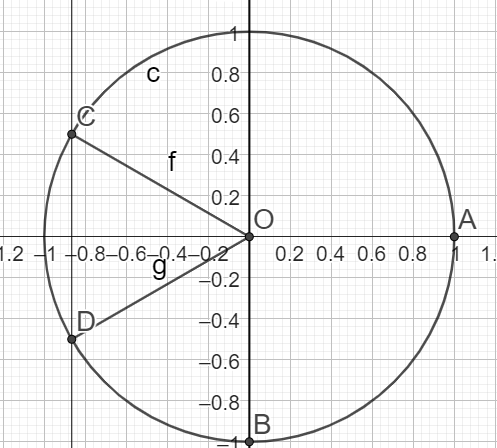
\(cos(x_1)=\frac{-\sqrt{3}}{2}\)
Sur I=\(\mathbb{R}\)
\(\iff x_1 \in \{\pi - \frac{\pi}{6}+2k\pi ;\pi + \frac{\pi}{6}+2k\pi \}\)
\(\iff x_1 \in \{\frac{6\pi}{6} - \frac{\pi}{6}+2k\pi;\frac{6\pi}{6} + \frac{\pi}{6}+2k\pi \}\) \(k\in \mathbb{Z}\)
\(\iff x_1 \in \{\frac{5\pi}{6}+2k\pi;\frac{7\pi}{6}+2k\pi \}\) \(k\in \mathbb{Z}\)
\(\iff x_1 \in \{\frac{5\pi}{6}+2k\pi;\frac{7\pi}{6}+2k\pi \}\) \(k\in \mathbb{Z}\)
Sur J=\(]-2\pi;2\pi]\)
Pour \(k=0\)
\(\frac{5\pi}{6} \in ]-2\pi;2\pi]\)
\(\frac{7\pi}{6} \in ]-2\pi;2\pi]\)
Pour \(k=-1\)
\(\frac{5\pi}{6}-2\pi=\frac{5\pi}{6}-\frac{12\pi}{6}=-\frac{7\pi}{6} \in ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
\(\frac{7\pi}{6}-2\pi=\frac{7\pi}{6}-\frac{12\pi}{6}=\frac{-5\pi}{6} \in ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
Pour \(k=-2\)
\(\frac{5\pi}{6}-2 \times 2\pi=\frac{5\pi}{6}-4\pi=\frac{5\pi}{6}-\frac{24\pi}{6}=-\frac{19\pi}{6} \notin ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
\(\frac{7\pi}{6}-2 \times 2\pi=\frac{7\pi}{6}-4\pi=\frac{7\pi}{6}-\frac{24\pi}{6}=-\frac{17\pi}{6} \notin ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
Pour \(k=1\)
\(\frac{5\pi}{6}+2\pi= \frac{5\pi}{6}+\frac{12\pi}{6}=\frac{17\pi}{6} \notin ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
\(\frac{7\pi}{6}+2\pi= \frac{7\pi}{6}+\frac{12\pi}{6}=\frac{19\pi}{6} \notin ]-2\pi;2\pi]=]\frac{-12\pi}{6};\frac{12\pi}{6}]\)
donc \(S_1=\{ \frac{5\pi}{6} ;-\frac{7\pi}{6} ;\frac{-5\pi}{6} ;\frac{7\pi}{6} \}\)
\(\iff S_1=\{ -\frac{7\pi}{6}; -\frac{5\pi}{6}; \frac{5\pi}{6}; \frac{7\pi}{6} \}\)
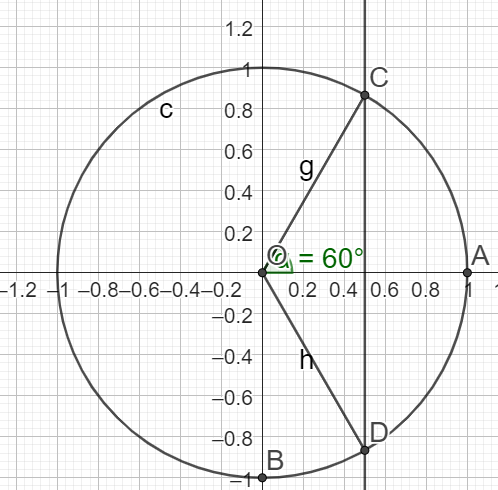
\(cos(x_2)=\frac{1}{2}\)
Sur I=\(\mathbb{R}\)
\(x_2 \in {\frac{\pi}{3}+2k\pi ;\frac{-\pi}{3}+2k\pi}\) \(k\in \mathbb{Z}\)
Sur J=\(]-2\pi;2\pi]\)
\(x_2 \in {\frac{\pi}{3}+2k\pi ;\frac{-\pi}{3}+2k\pi}\) \(k\in \mathbb{Z}\)
Pour \(k\)=0: \(\frac{\pi}{3} \in ]-2\pi;2\pi]\)
Pour \(k\)=-1: \(\frac{\pi}{3}-2\pi=\frac{\pi}{3}-\frac{6\pi}{3}=-\frac{5\pi}{3} \in ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
Pour \(k\)=-2: \(\frac{\pi}{3}-2 \times 2\pi=\frac{\pi}{3}-4\pi=\frac{\pi}{3}-\frac{12\pi}{3}=-\frac{11\pi}{3} \notin ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
Pour \(k\)=1: \(\frac{\pi}{3}+2\pi= \frac{\pi}{3}+\frac{6\pi}{3}=\frac{7\pi}{3} \notin ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
Pour \(k\)=0: \(-\frac{\pi}{3} \in ]-2\pi;2\pi]\)
Pour \(k\)=-1: \(\frac{-\pi}{3}-2\pi=\frac{-\pi}{3}-\frac{6\pi}{3}=\frac{-7\pi}{3} \notin ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
Pour \(k\)=1:
\(\frac{-\pi}{3}+2\pi=\frac{-\pi}{3}+\frac{6\pi}{3}=\frac{5\pi}{3} \in ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
Pour \(k\)=2:
\(\frac{-\pi}{3}+2 \times 2\pi=\frac{-\pi}{3}+\frac{12\pi}{3}=\frac{11\pi}{3} \notin ]-2\pi;2\pi]=]\frac{-6\pi}{3};\frac{6\pi}{3}]\)
donc \(S_2=\{\frac{\pi}{3} ;-\frac{5\pi}{3} ;\frac{-\pi}{3}; \frac{5\pi}{3} \}\)
Finalement les solutions de l'équation sur \(]-2\pi ;2\pi]\)
sont :
\(S_1 \cup S_2 =\{-\frac{7\pi}{6};-\frac{5\pi}{6};\frac{5\pi}{6};\frac{7\pi}{6} \} \cup \{ \frac{\pi}{3} ;-\frac{5\pi}{3} ;\frac{-\pi}{3} ; \frac{5\pi}{3} \}\)
\(\iff S_1 \cup S_2 =\{ -\frac{5\pi}{3}; -\frac{7\pi}{6};-\frac{5\pi}{6} ;\frac{-\pi}{3}; \frac{\pi}{3}; \frac{5\pi}{6}; \frac{7\pi}{6} ; \frac{5\pi}{3} \}\)
Question
4.\(cos(x) \le \frac{-1}{2}\) sur I=\(]0;2\pi]\)
Solution
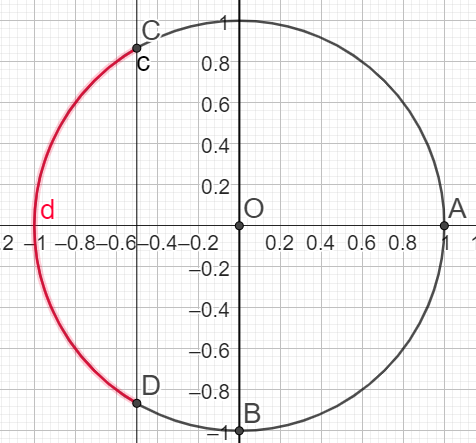
\(x \in [\pi-\frac{\pi}{3} ;\pi+\frac{\pi}{3}]\)
\(\iff x \in [\frac{3\pi}{3}-\frac{\pi}{3} ;\frac{3\pi}{3}+\frac{\pi}{3}]\)
\(\iff x \in [\frac{2\pi}{3} ;\frac{4\pi}{3}]\)
Question
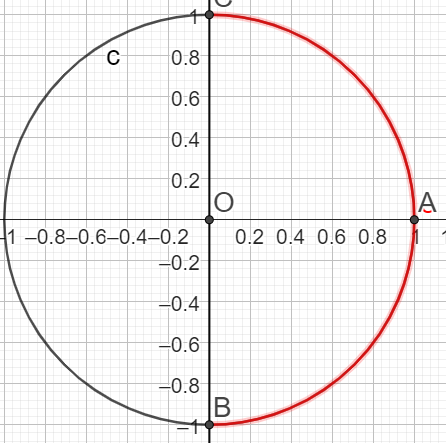
5.\(sin(x) \le \frac{\sqrt{2}}{2}\)sur I=\(]-\pi :\pi]\)
Solution
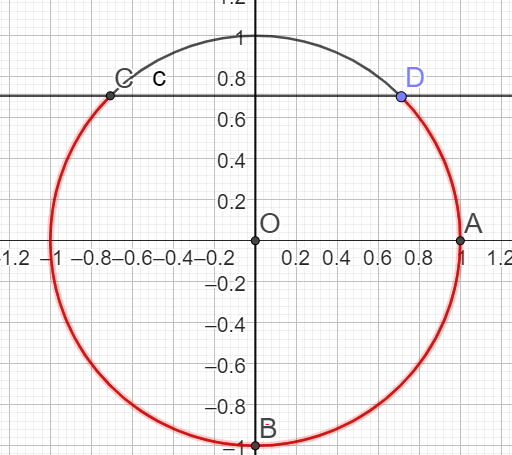
\(x \in ]-\pi ;\frac{\pi}{4}] \cup [\frac{\pi}{2}+\frac{\pi}{4};\pi]\)
\(\iff x \in ]-\pi ;\frac{\pi}{4}] \cup [\frac{2\pi}{4}+\frac{\pi}{4};\pi]\)
\(\iff x \in ]-\pi ;\frac{\pi}{4}] \cup [\frac{3\pi}{4};\pi]\)
Question
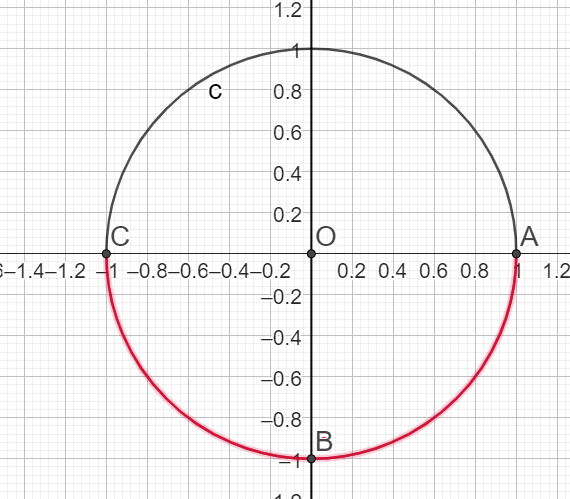
6.\(cos(x) \le \frac{\sqrt{3}}{2}\) sur I=\(]-\pi ;\pi]\)
Solution
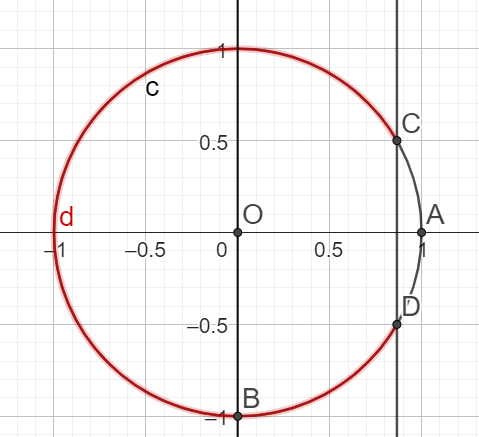
\(x \in ]-\pi ;-\frac{\pi}{6}] \cup [\frac{\pi}{6};\pi]\)
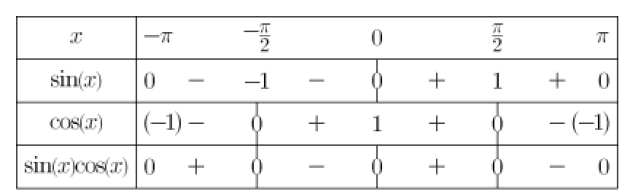
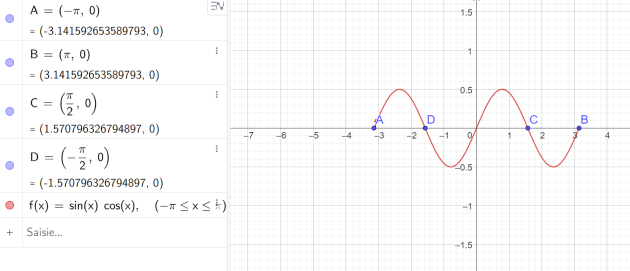
Question
7.\(sin(x)cos(x)<0\) sur I=\(]-\pi ;\pi]\)