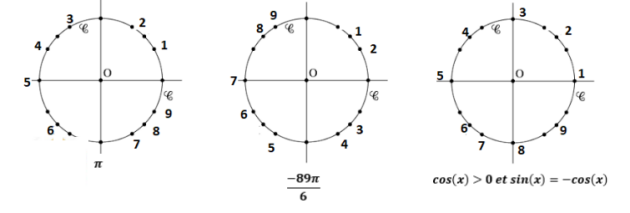
Exercice : Mastermind 2025
On cherche un code à trois chiffres.
Voici cinq indices, chacun composé de trois mystères à résoudre :
la position du nombre cherché vous donnera le chiffre à trouver.
Pour chaque indice, une indication permet de savoir si le code ainsi obtenu a
(ou n’a pas) des chiffres en commun avec le code recherché.
En utilisant ces cinq indices, déterminer le code à trois chiffres
Question
Indice 1 : un chiffre est correct et bien placé
Indice
2 9 1
Solution
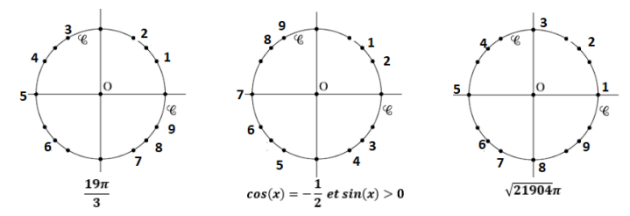
\(\frac{\frac{19\pi}{3}}{2\pi}=\frac{\frac{19\pi}{3}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{19\pi}{3}}{2\pi}=\frac{19\pi}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{19\pi}{3}}{2\pi}=\frac{19\pi}{6\pi}\)
\(\iff \frac{\frac{19\pi}{3}}{2\pi}=\frac{19}{6}=\frac{18}{6}+\frac{1}{6}\)
\(\iff \frac{\frac{19\pi}{3}}{2\pi}=3+\frac{1}{6}\)
donc \(\frac{19\pi}{3}\) représente 3 tours et \(\frac{1}{6}\) de tour.
\(\frac{19\pi}{3}\) et \(\frac{1}{6} \times 2\pi=\frac{2\pi}{6}\) représentent le même angle
donc \(\frac{19\pi}{3}\) et \(\frac{\pi}{3}\) représentent le même angle
or l'angle de \(\frac{\pi}{3}\) correspond à l'angle de \(\frac{180}{3}=60°\)
soit l'\(\color{magenta}{\text{angle 2}}\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\)
\(cos(x)=-\frac{1}{2} \iff x=\pi-\frac{\pi}{3}=\frac{3\pi}{3}-\frac{\pi}{3}=\frac{2\pi}{3}\) ou \(x=-\frac{2\pi}{3}\)
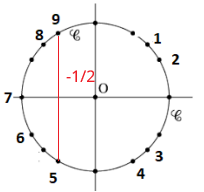
or \(sin(-\frac{2\pi}{3})=-\frac{\sqrt{3}}{2}\) et \(sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}\)
Finalement \(x=\frac{2\pi}{3}\) car \(sin(x)>0\)
soit l'\(\color{magenta}{\text{angle 9}}\)
\(\sqrt{21904}\pi=148\pi=74 \times 2\pi\)
donc cette mesure correspond à l'angle nul
soit l'\(\color{magenta}{\text{angle 1}}\)
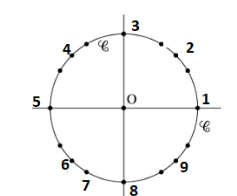
Question
Indice 2 : un chiffre est correct et mal placé
Indice
2 4 5
Solution
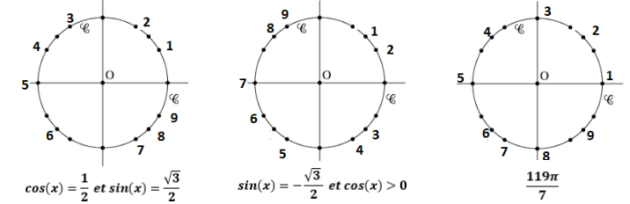
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\) :
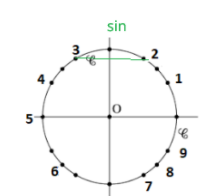
\(cos(x)=\frac{1}{2} \iff x=\frac{\pi}{3}\) ou \(x=-\frac{\pi}{3}\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\) :
\(sin(x)=\frac{\sqrt{3}}{2} \iff x=\pi-\frac{\pi}{3}=\frac{3\pi}{3}-\frac{\pi}{3}=\frac{2\pi}{3}\) ou \(x=\frac{\pi}{3}\)
Finalement : \(x=\frac{\pi}{3}\) soit l'\(\color{magenta}{\text{angle 2}}\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\) :
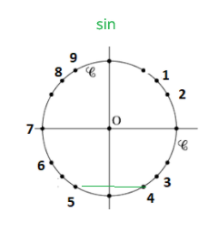
\(sin(x)=-\frac{\sqrt{3}}{2} \iff x=-\frac{2\pi}{3}\) ou \(x=-\frac{\pi}{3}\)
\(cos(x)>0 \iff \in ]-\frac{\pi}{2} ;\frac{\pi}{2}[\)
Finalement : \(x=-\frac{\pi}{3}\) soit l'\(\color{magenta}{\text{angle 4}}\)
\(\frac{\frac{119\pi}{7}}{2\pi}=\frac{\frac{119\pi}{7}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{119\pi}{7}}{2\pi}=\frac{119\pi}{7} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{119\pi}{7}}{2\pi}=\frac{119\pi}{14\pi}\)
\(\iff \frac{\frac{119\pi}{7}}{2\pi}=\frac{119}{14}=8,5\)
\(\frac{119\pi}{7}-8 \times 2\pi\)
\(=\frac{119\pi}{7}-16\pi\)
\(=\frac{119\pi}{7}-\frac{112\pi}{7}\)
\(=\frac{7\pi}{7}=\pi\)
soit l'\(\color{magenta}{\text{angle 5}}\)
Question
Indice 3 : deux chiffres sont corrects mais mal placés
Indice
4 1 3
Solution
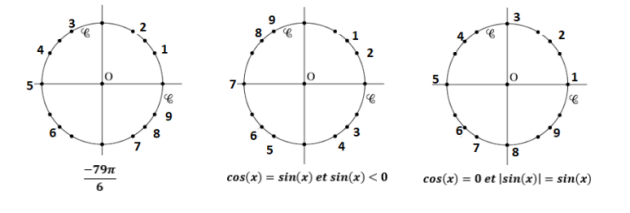
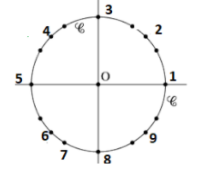
\(\frac{\frac{-79\pi}{6}}{2\pi}=\frac{\frac{-79\pi}{6}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{-79\pi}{6}}{2\pi}=\frac{-79\pi}{6} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-79\pi}{6}}{2\pi}=\frac{-79\pi}{12\pi}\)
\(\iff \frac{\frac{-79\pi}{6}}{2\pi}=\frac{-79}{12}=\frac{-72}{12}+\frac{-7}{12}\)
\(\iff \frac{\frac{-79\pi}{6}}{2\pi}=\frac{-79}{12}=-6+\frac{-7}{12}\)
\(\frac{-79\pi}{6}+6 \times 2\pi\)
\(=\frac{-79\pi}{6}+12\pi\)
\(=\frac{-79\pi}{6}+\frac{72\pi}{6}\)
\(=\frac{-7\pi}{6}\)
soit l'\(\color{magenta}{\text{angle 4}}\)
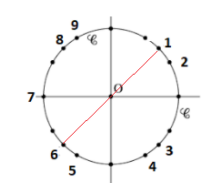
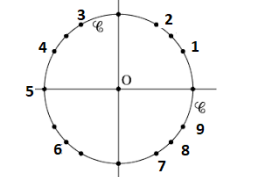
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
les fonctions cosinus et sinus sont égales pour :
\(cos(\frac{\pi}{4})=sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\) et \(cos(-\frac{3\pi}{4})=sin(-\frac{3\pi}{4})=-\frac{\sqrt{2}}{2}\)
or \(sin(x)>0\) donc la mesure de l'angle est \(\frac{\pi}{4}\)
soit l'\(\color{magenta}{\text{angle 1}}\)
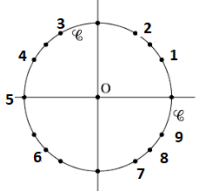
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
\(cos(x)=0 \iff x=\frac{\pi}{2}\) ou \(x=-\frac{\pi}{2}\)
\(sin(-\frac{\pi}{2})=-1\) et \(|sin(-\frac{\pi}{2})|=|-1|=1\)
donc \(|sin(-\frac{\pi}{2})|\ne sin(-\frac{\pi}{2})\)
\(sin(\frac{\pi}{2})=1\) et \(|sin(\frac{\pi}{2})|=|1|=1\)
donc \(|sin(\frac{\pi}{2})|= sin(\frac{\pi}{2})\)
Finalement : \(x=\frac{\pi}{2}\) soit l'\(\color{magenta}{\text{angle 3}}\)
Question
Indice 4 : il n’y a rien de juste
Indice
5 7 8
Solution
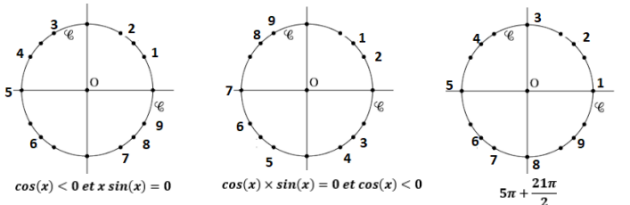
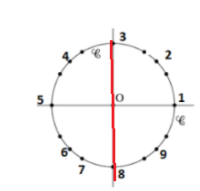
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
\(cos(x)<0 \iff x \in ]-\pi ;\frac{-\pi}{2}[ \cup ]\frac{\pi}{2} ;\pi[\)
\(x \times sin(x)=0\)
D'après le théorème du produit nul :
\(\color{red}{\text{Un produit de facteurs est nul}}\)
\(\color{red}{\text{si et seulement si }}\)
\(\color{red}{\text{un des facteurs au moins est nul.}}\)
\(x=0\) ou \(sin(x)=0\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
\(x=0\) ou \(x=0\) ou \(x=\pi\)
Finalement : \(x=\pi\) soit l'\(\color{magenta}{\text{angle 5}}\)
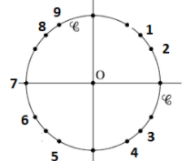
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
\(cos(x)<0 \iff x \in ]-\pi ;\frac{-\pi}{2}[ \cup ]\frac{\pi}{2} ;\pi[\)
\(cos(x) \times sin(x)=0\)
D'après le théorème du produit nul :
\(\color{red}{\text{Un produit de facteurs est nul}}\)
\(\color{red}{\text{si et seulement si }}\)
\(\color{red}{\text{un des facteurs au moins est nul.}}\)
\(cos(x)=0\) ou \(sin(x)=0\)
or \(cos(x)<0\) donc \(sin(x)=0\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\),
\(x=0\) ou \(x=\pi\)
Finalement : \(x=\pi\) soit l'\(\color{magenta}{\text{angle 7}}\)
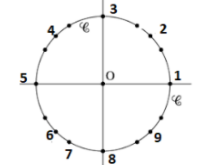
\(5\pi + \frac{21\pi}{2}=5\pi + 10,5\pi=15,5\pi=16\pi - 0,5\pi\)
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\)
\(5\pi + \frac{21\pi}{2}\) correspond donc à l'angle \(- 0,5\pi=\frac{-\pi}{2}\)
soit l'\(\color{magenta}{\text{angle 8}}\)
Question
Indice 5 : un chiffre est correct et mal placé
Indice
5 6 9
Solution
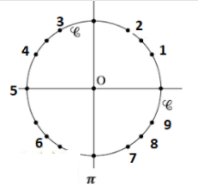
\(\pi\) soit l'\(\color{magenta}{\text{angle 5}}\)
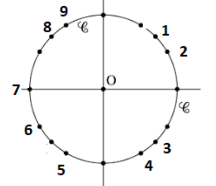
\(\frac{\frac{-89\pi}{6}}{2\pi}=\frac{\frac{-89\pi}{6}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{-89\pi}{6}}{2\pi}=\frac{-89\pi}{6} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-89\pi}{6}}{2\pi}=\frac{-89\pi}{12\pi}\)
\(\iff \frac{\frac{-89\pi}{6}}{2\pi}=\frac{-89}{12}=\frac{-84}{12}+\frac{-5}{12}\)
\(\iff \frac{\frac{-89\pi}{6}}{2\pi}=-7+\frac{-5}{12}\)
\(\frac{-89\pi}{6}+7 \times 2\pi\)
\(=\frac{-89\pi}{6}+14\pi\)
\(=\frac{-89\pi}{6}+\frac{84\pi}{6}\)
\(=\frac{-5\pi}{6}\)
soit l'\(\color{magenta}{\text{angle 6}}\)
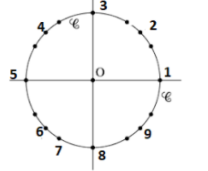
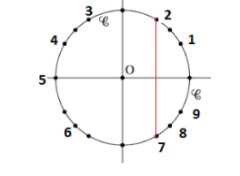
Dans l'intervalle des mesures principales \(]-\pi ;\pi]\) :
\(cos(x)>0 \iff \in ]-\frac{\pi}{2} ;\frac{\pi}{2}[\)
\(sin(\frac{3\pi}{4})=-cos(\frac{3\pi}{4})=\frac{\sqrt{2}}{2}\)
\(sin(\frac{-\pi}{4})=-cos(\frac{-\pi}{4})=\frac{-\sqrt{2}}{2}\)
Finalement l'angle est \(\frac{-\pi}{4}\)
soit l'\(\color{magenta}{\text{angle 9}}\)
Question
Code Final
Solution
3 9 4