Exercice : Fractions
Calculer les dérivées respectives des fonctions suivantes, spécifier leur ensemble de définition :
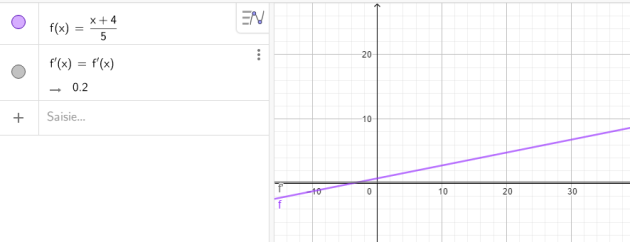
Question
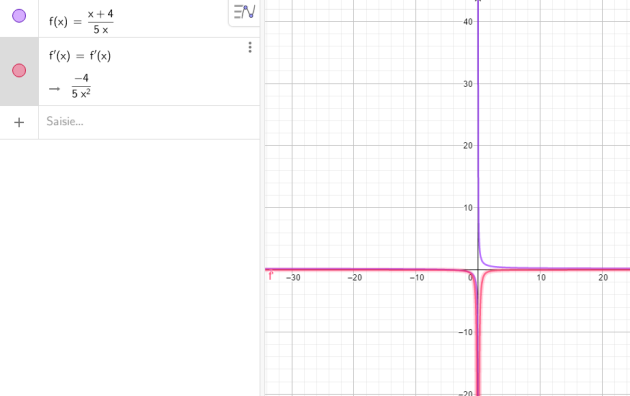
Question
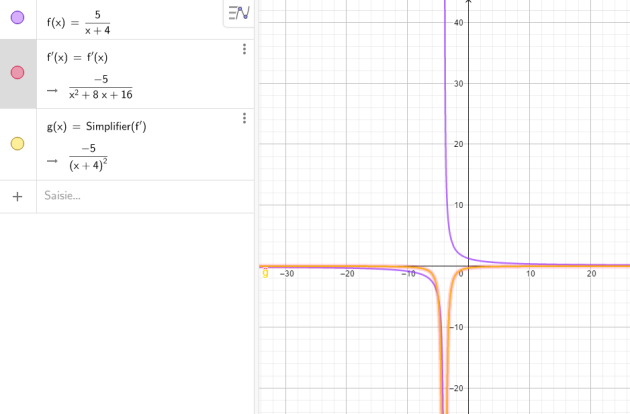
Question
Question
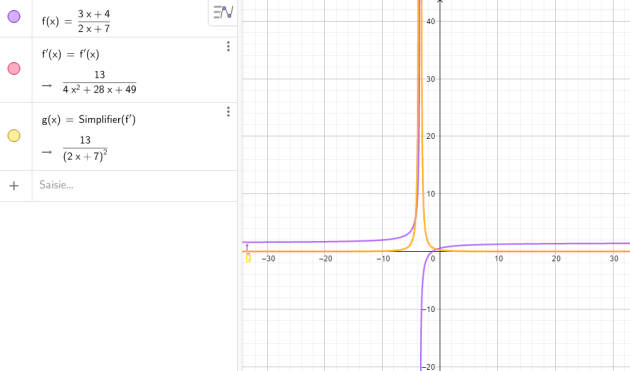
\(d(x) =\frac{3x+4}{2x+7}\)
Indice
\(x\mapsto 1\)
\(k\mapsto 0\)
\(ku\mapsto ku'\)
\(u+v\mapsto u'+v'\)
\(\frac{u}{v}\mapsto \frac{u'v-uv'}{v^2}\)
Solution
\(\begin{cases}u=3x+4\\v=2x+7\end{cases}\)
\(\begin{cases}u'=3\\v'=2\end{cases}\)
\(d'(x)=\frac{3(2x+7)-(3x+4)\times 2}{(2x+7)^2}\)
\(\iff d'(x)=\frac{6x+21-(6x+8)}{(2x+7)^2}\)
\(\iff d'(x)=\frac{6x+21-6x-8}{(2x+7)^2}\)
\(\iff d'(x)=\frac{13}{(2x+7)^2}\)
\(2x+7=0\iff 2x=-7 \iff x=-\frac{7}{2}=-3,5\)
\(D_c=\mathbb{R}\backslash\{-3,5\}\) et \(D_{C'}=\mathbb{R}\backslash\{-3,5\}\)