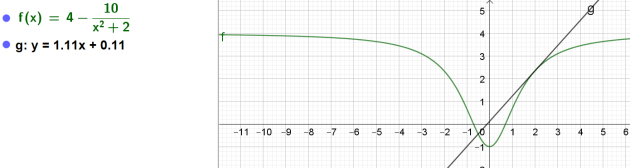
Exercice : Exercice en devoir Maison
Question
2.Déterminer les équations puis tracer les tangentes à la courbe représentative de la fonction g aux points d'abscisses :
Question
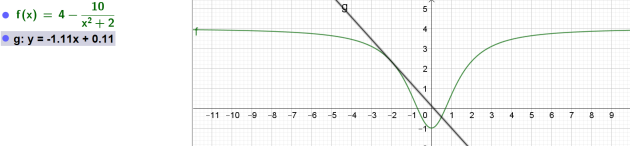
a. \(x_1=−2\)
Solution
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(a\) est :
\(y=g'(a)(x-a)+g(a)\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(-2\) est :
\(y=g'(-2)(x-(-2))+g(-2)\)
Calcul de \(g'(-2)\):
\(g'(-2) = \frac{20 \times (-2)}{((-2)^2 + 2)^2}\)
\(\iff g'(-2) = \frac{-40}{(4+ 2)^2}\)
\(\iff g'(-2) = \frac{-40}{6^2}\)
\(\iff g'(-2) = \frac{-40}{36}= \frac{-10}{9}\)
Calcul de \(g(-2)\):
\(g(-2)= 4 −\frac{10}{(-2)^2 + 2}\)
\(\iff g(-2)= 4 −\frac{10}{4 + 2}\)
\(\iff g(-2)= 4 −\frac{10}{6}\)
\(\iff g(-2)= 4 −\frac{5}{3}\)
\(\iff g(-2)= \frac{12}{3} −\frac{5}{3}\)
\(\iff g(-2)= \frac{7}{3}\)
\(y=g'(-2)(x-(-2))+g(-2)= \frac{-10}{9}(x+2)+\frac{7}{3}\)
\(\iff y= \frac{-10}{9}x+\frac{-20}{9}+\frac{7}{3}\)
\(\iff y= \frac{-10}{9}x+\frac{-20}{9}+\frac{21}{9}\)
\(\iff y= \frac{-10}{9}x+\frac{1}{9}\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(-2\) est donc
\(y= \frac{-10}{9}x+\frac{1}{9}\)
Question
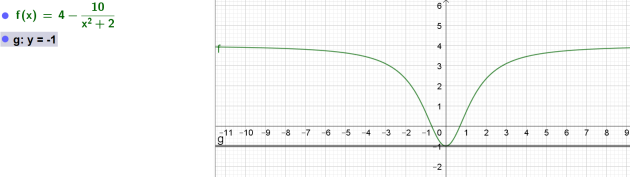
b. \(x_2=0\)
Solution
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(a\) est :
\(y=g'(a)(x-a)+g(a)\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(0\) est :
\(y=g'(0)(x-0)+g(0)\)
Calcul de \(g'(0)\):
\(g'(0) = \frac{20 \times 0}{(0^2 + 2)^2}\)
\(\iff g'(0) = \frac{0}{2^2}\)
\(\iff g'(0) = 0\)
Calcul de \(g(0)\):
\(g(0)= 4 −\frac{10}{0^2 + 2}\)
\(\iff g(0)= 4 −\frac{10}{ 2}\)
\(\iff g(0)= 4 −5\)
\(\iff g(0)= -1\)
\(y=g'(0)(x-0)+g(0)=0x+(-1)=-1\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(0\) est donc
\(y= -1\)
Question
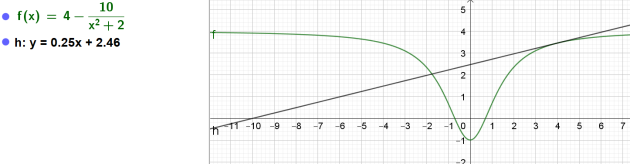
c. \(x_3=4\)
Solution
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(a\) est :
\(y=g'(a)(x-a)+g(a)\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(4\) est :
\(y=g'(4)(x-4)+g(4)\)
Calcul de \(g'(4)\):
\(g'(4) = \frac{20 \times 4}{(4^2 + 2)^2}\)
\(\iff g'(4) = \frac{80}{(16+2)^2}\)
\(\iff g'(4) = \frac{80}{18^2}\)
\(\iff g'(4) = \frac{80}{324}=\frac{20}{81}\)
Calcul de \(g(4)\):
\(g(4)= 4 −\frac{10}{4^2 + 2}\)
\(\iff g(4)= 4 −\frac{10}{ 16+2}\)
\(\iff g(4)= 4 −\frac{10}{ 18}\)
\(\iff g(4)= 4-\frac{5}{9}\)
\(\iff g(4)= \frac{36}{9}-\frac{5}{9}\)
\(\iff g(4)= \frac{31}{9}\)
\(y=g'(4)(x-4)+g(4)=\frac{20}{81}(x-4)+\frac{31}{9}\)
\(\iff y=\frac{20}{81}(x-4)+\frac{31}{9}\)
\(\iff y=\frac{20}{81}x-\frac{80}{81}+\frac{279}{81}\)
\(\iff y=\frac{20}{81}x+\frac{199}{81}\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(4\) est donc
\(y= \frac{20}{81}x+\frac{199}{81}\)
Question
2. Calculer l'équation de la tangente à la courbe représentative de la fonction \(g\) au point d'abscisse \(x_4=2\).Tracer cette tangente.
Solution
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(a\) est :
\(y=g'(a)(x-a)+g(a)\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(2\) est :
\(y=g'(2)(x-2)+g(2)\)
Calcul de \(g'(2)\):
\(g'(2) = \frac{20 \times 2}{(2^2 + 2)^2}\)
\(\iff g'(2) = \frac{40}{(4+ 2)^2}\)
\(\iff g'(2) = \frac{40}{6^2}\)
\(\iff g'(-2) = \frac{40}{36}= \frac{10}{9}\)
Calcul de \(g(2)\):
\(g(2)= 4 −\frac{10}{2^2 + 2}\)
\(\iff g(2)= 4 −\frac{10}{4 + 2}\)
\(\iff g(2)= 4 −\frac{10}{6}\)
\(\iff g(2)= 4 −\frac{5}{3}\)
\(\iff g(2)= \frac{12}{3} −\frac{5}{3}\)
\(\iff g(2)= \frac{7}{3}\)
\(y=g'(2)(x-2)+g(2)= \frac{10}{9}(x-2)+\frac{7}{3}\)
\(\iff y= \frac{10}{9}x-\frac{20}{9}+\frac{7}{3}\)
\(\iff y= \frac{10}{9}x+\frac{-20}{9}+\frac{21}{9}\)
\(\iff y= \frac{10}{9}x+\frac{1}{9}\)
L'équation de la tangente à la fonction \(g\) au point d'abscisse \(2\) est donc
\(y= \frac{10}{9}x+\frac{1}{9}\)