Exercice : Polynômes 2
Calculer les dérivées respectives des fonctions suivantes et donner leurs ensembles de définitions :
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
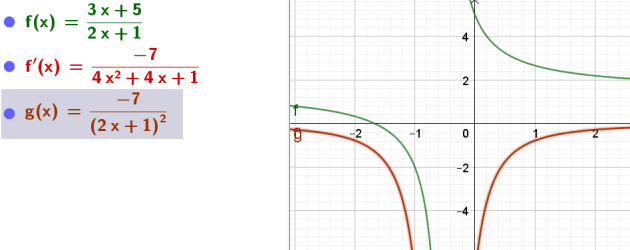
\(j( x ) =\frac{3x+5}{2x+1}\)
Indice
\(x \mapsto 1\)
\(k\mapsto 0\)
\(ku\mapsto ku'\)
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(u+v\mapsto u'+v'\)
Solution
\(\begin{cases}u=3x+5\\v=2x+1\end{cases}\)
\(\begin{cases}u'=3\\v'=2\end{cases}\)
\(j'( x ) =\frac{3(2x+1)-2(3x+5)}{(2x+1)^2}\)
\(\iff j'( x ) =\frac{6x+3-6x-10}{(2x+1)^2}\)
\(\iff j'( x ) =\frac{-7}{(2x+1)^2}\)
\(2x+1=0\)
\(\iff 2x=-1\)
\(\iff x=-\frac{1}{2}\)
\(D_j=\mathbb{R}\backslash\{-\frac{1}{2}\}\) et \(D_{j'}=\mathbb{R}\backslash\{-\frac{1}{2}\}\)
Question
Question
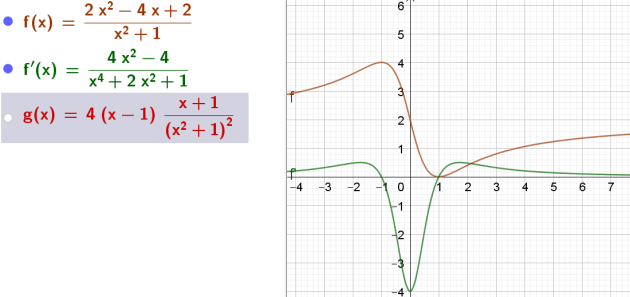
\(l(x)=\frac{2x^{2}-4x+2}{x^{2}+1}\)
Indice
\(x^n\mapsto nx^{n-1}\)
\(x \mapsto 1\)
\(k\mapsto 0\)
\(ku\mapsto ku'\)
\(u+v\mapsto u'+v'\)
\(\frac{u}{v}\mapsto \frac{u'v-uv'}{v^2}\)
Solution
\(\begin{cases}u=2x^{2}-4x+2\\v=x^{2}+1\end{cases}\)
\(\begin{cases}u'=2 \times 2x-4\times 1\\v'=2x\end{cases}\)
\(\iff \begin{cases}u'=4x-4\\v'=2x\end{cases}\)
\(l'(x)=\frac{(4x-4)(x^2+1)-2x(2x^{2}-4x+2)}{(x^{2}+1)^2}\)
\(\iff l'(x)=\frac{(4x^3+4x-4x^2-4)-4x^{3}+8x^2-4x}{(x^{2}+1)^2}\)
\(\iff l'(x)=\frac{4x^3+4x-4x^2-4-4x^{3}+8x^2-4x}{(x^{2}+1)^2}\)
\(\iff l'(x)=\frac{4x^2-4}{(x^{2}+1)^2}\)
\(\iff l'(x)=\frac{4(x+1)(x-1)}{(x^{2}+1)^2}\)
\(x^{2}+1\) est une forme factorisée qui nous permet de savoir que le sommet de cette parabole est le point de coordonnées (0;1)
donc le dénominateur ne s’annule pas.
\(D_l=\mathbb{R}\) et \(D_{l'}=\mathbb{R}\)
Question
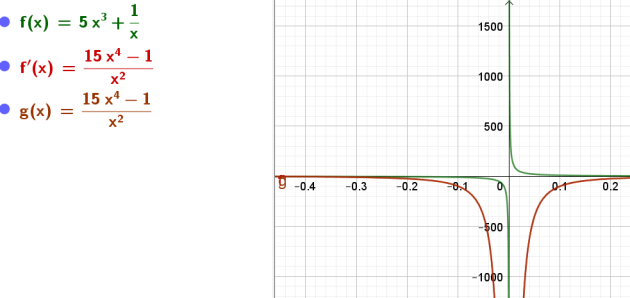
\(m(x)=x^{2021}-\frac{2021}{x}+2021\sqrt{x}\)
Indice
\(x^n\mapsto nx^{n-1}\)
\(\sqrt{x} \mapsto \frac{1}{2\sqrt{x}}\)
\(\frac{1}{x} \mapsto \frac{-1}{x^2}\)
\(k\mapsto 0\)
\(ku\mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(m'(x)=2021x^{2020}-2021\times \frac{-1}{x^2}+2021\times \frac{1}{2\sqrt{x}}\)
\(\iff m'(x)=2021x^{2020}+\frac{2021}{x^2}+\frac{2021}{2\sqrt{x}}\)
\(D_m=]0 ;+\infty[\) et \(D_{m'}=]0;+\infty[\)
Question
Question
\(o( x ) =\frac{3x+5}{2x+1}\)
Indice
\(x \mapsto 1\)
\(k\mapsto 0\)
\(ku\mapsto ku'\)
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(u+v\mapsto u'+v'\)
Solution
\(\begin{cases}u=3x+5\\v=2x+1\end{cases}\)
\(\begin{cases}u'=3\\v'=2\end{cases}\)
\(o'( x ) =\frac{3(2x+1)-2(3x+5)}{(2x+1)^2}\)
\(\iff o'( x ) =\frac{6x+3-6x-10}{(2x+1)^2}\)
\(\iff o'( x ) =\frac{-7}{(2x+1)^2}\)
\(2x+1=0\)
\(\iff 2x=-1\)
\(\iff x=-\frac{1}{2}\)
\(D_o=\mathbb{R}\backslash\{-\frac{1}{2}\}\) et \(D_{o'}=\mathbb{R}\backslash\{-\frac{1}{2}\}\)
Question
Question
Question
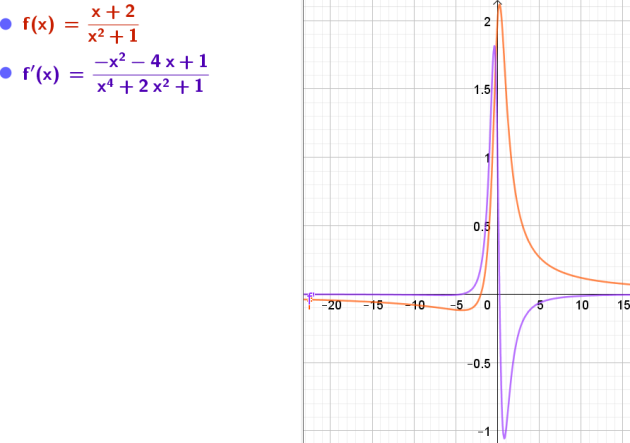
\(r(s) = \frac{s + 2}{s^2 + 1}\)
Indice
\(x \mapsto 1\)
\(u+v \mapsto u'+v'\)
\(x^n \mapsto nx^{n-1}\)
\(ku\mapsto ku'\)
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
Solution
\(\begin{cases}u=s+2\\v=s^2 + 1\end{cases}\)
\(\begin{cases}u'=1\\v'=2s\end{cases}\)
\(r'(s) = \frac{1(s^2 + 1)-(s+2) \times 2s}{(s^2 + 1)^2}\)
\(\iff r'(s) = \frac{s^2 + 1-(2s^2+4s)}{(s^2 + 1)^2}\)
\(\iff r'(s) = \frac{s^2 + 1-2s^2-4s}{(s^2 + 1)^2}\)
\(\iff r'(s) = \frac{-s^2-4s+1}{(s^2 + 1)^2}\)
\(s^2+1\) est une forme canonique donc le sommet de la parabole d'équation \(s^2+1\) est (0;1)
donc pour tout \(s\in\mathbb{R}\) \(s^2+1\ge1\)
L'équation \(s^2 + 1=0\) n'admet donc pas de solution.
\(D_r=\mathbb{R}\) et \(D_{r'}=\mathbb{R}\)