Exercice : Valeurs 2
Question
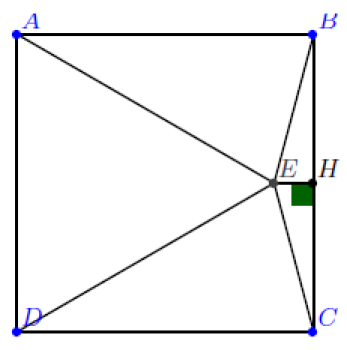
1. Démontrer que \((\overrightarrow{CB};\overrightarrow{CE})=\frac{\pi}{12}.\)
Indice
ABCD est un carré de côté 1 et AED est le triangle équilatéral représenté ci-dessous.
Solution
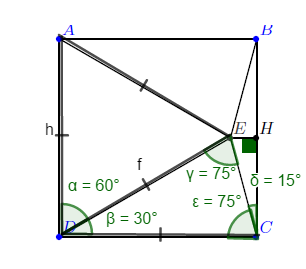
Le triangle AED est équilatéral donc \((\vec{DE},\vec{DA})=\frac{\pi}{3}\)
ABCD est un carré donc \((\vec{DC},\vec{DA})=\frac{\pi}{2}\)
\((\vec{DC},\vec{DE})=(\vec{DC},\vec{DA})-(\vec{DE},\vec{DA})=\frac{\pi}{2}-\frac{\pi}{3}\)
\(\iff (\vec{DC},\vec{DE})=\frac{3\pi}{6}-\frac{2\pi}{6}=\frac{\pi}{6}\)
DE=DA=DC donc le triangle DCE est isocèle en D donc
\((\vec{CE},\vec{CD})=(\vec{ED},\vec{EC})\)
or
\((\vec{CE},\vec{CD})+(\vec{ED},\vec{EC})+(\vec{DC},\vec{DE})=\pi\)
\(\iff 2(\vec{CE},\vec{CD})+\frac{\pi}{6}=\pi\)
\(\iff 2(\vec{CE},\vec{CD})=\pi-\frac{\pi}{6}\)
\(\iff 2(\vec{CE},\vec{CD})=\frac{6\pi}{6}-\frac{\pi}{6}\)
\(\iff 2(\vec{CE},\vec{CD})=\frac{5\pi}{6}\)
\(\iff (\vec{CE},\vec{CD})=\frac{5\pi}{12}\)
ABCD est un carré donc \((\vec{CB},\vec{CD})=\frac{\pi}{2}\)
\((\vec{CB},\vec{CD})=(\vec{CB},\vec{CE})+(\vec{CE},\vec{CD})=\frac{\pi}{2}\)
\(\iff (\vec{CB},\vec{CD})=(\vec{CB},\vec{CE})+\frac{5\pi}{12}=\frac{\pi}{2}\)
\(\iff (\vec{CB},\vec{CE})+\frac{5\pi}{12}=\frac{\pi}{2}\)
\(\iff (\vec{CB},\vec{CE})=\frac{\pi}{2}-\frac{5\pi}{12}\)
\(\iff (\vec{CB},\vec{CE})=\frac{6\pi}{12}-\frac{5\pi}{12}\)
\(\iff (\vec{CB},\vec{CE})=\frac{\pi}{12}\)
Question
2. Calculer les longueurs CH puis CE.
Solution
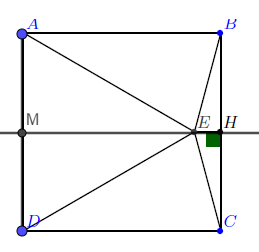
\(CH=DM=\frac{1}{2}\) par symétrie
\(HE=HM-EM\)
\(\iff HE=HM-EM\)
\(\iff HE=1-\frac{\sqrt{3}}{2}\)
Le triangle EHC est rectangle en H d'hypoténuse [CE]
d'après le théorème de Pythagore :
\(HE^2+HC^2=CE^2\)
\(\iff (1-\frac{\sqrt{3}}{2})^2+(\frac{1}{2})^2=CE^2\)
\(\iff 1-\sqrt{3}+\frac{3}{4}+\frac{1}{4}=CE^2\)
\(\iff 1-\sqrt{3}+\frac{4}{4}=CE^2\)
\(\iff 2-\sqrt{3}=CE^2\)
\(\iff \sqrt{2-\sqrt{3}}=CE\)
Question
3. En déduire que \(cos\frac{\pi}{12}=\frac{\sqrt{2+\sqrt{3}}}{2}\)
Solution
\(cos\frac{\pi}{12}=\frac{CH}{CE}=\frac{\frac{1}{2}}{\sqrt{2-\sqrt{3}}}\)
\(\iff cos\frac{\pi}{12}=\frac{CH}{CE}=\frac{\frac{1}{2}}{\frac{\sqrt{2-\sqrt{3}}{1}}\)
\(cos\frac{\pi}{12}=\frac{1}{2} \times \frac{1}{\sqrt{2-\sqrt{3}}}}\)
Question
4. Calculer \(sin\frac{\pi}{12}\), puis le sinus et le cosinus de\( \frac{5\pi}{12}.\)