Exercice : Valeurs 3
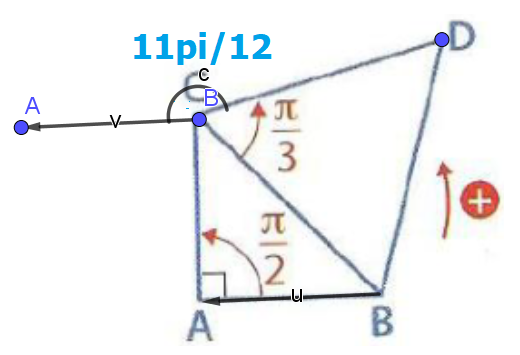
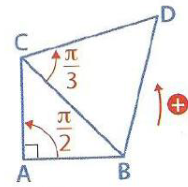
ABC est un triangle rectangle isocèle et BCD est un triangle équilatéral tels que :
\((\vec{AB} ;\vec{AC})=\frac{\pi}{2}\)
et
\((\vec{CB} ;\vec{CD})=\frac{\pi}{3}\)
Question
1.Justifier l'égalité :
\((\vec{CD} ;\vec{BA})=(\vec{CD} ;\vec{CB})+(\vec{BC} ;\vec{BA})+\pi\)
Solution
\((\vec{CD} ;\vec{BA})=(\vec{CD} ;\vec{CB})+(\vec{CB} ;\vec{BA})\)
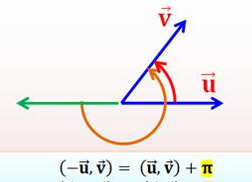
\(\iff (\vec{CD} ;\vec{BA})=(\vec{CD} ;\vec{CB})+(\vec{BC} ;\vec{BA})+\pi\)
Question
2.Déduisez-en la mesure principale de :
\((\vec{CD} ;\vec{BA})\)
Solution
\((\vec{CD} ;\vec{BA})=(\vec{CD} ;\vec{CB})+(\vec{BC} ;\vec{BA})+\pi\)
\(\iff (\vec{CD} ;\vec{BA})=-\frac{\pi}{3}+\frac{\pi}{4}+\pi\)
\(\iff (\vec{CD} ;\vec{BA})=-\frac{4\pi}{12}+\frac{3\pi}{12}+\frac{12\pi}{12}\)
\(\iff (\vec{CD} ;\vec{BA})=\frac{11\pi}{12}\)