Exercice : Valeurs 4
ABC est un triangle équilatéral tel que :
\((\vec{AB} ;\vec{AC})=\frac{\pi}{3}\)
ACD et BAE sont deux triangles rectangles isocèles tels que :
\((\vec{CA} ;\vec{CD})=\frac{\pi}{2}\)
et
\((\vec{AE} ;\vec{AB})=\frac{\pi}{2}\)
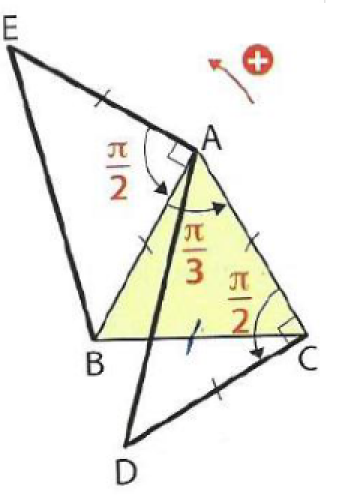
Question
1.Quelle est la mesure principale de
\((\vec{BA} ;\vec{BE})\)?
Solution
\((\vec{BA} ;\vec{BE})+(\vec{EB} ;\vec{EA})+(\vec{AE} ;\vec{AB})=\pi\)
\(2(\vec{BA} ;\vec{BE})+\frac{\pi}{2}=\pi\)
\(\iff 2(\vec{BA} ;\vec{BE})=\pi-\frac{\pi}{2}\)
\(\iff 2(\vec{BA} ;\vec{BE})=\frac{\pi}{2}\)
\(\iff (\vec{BA} ;\vec{BE})=\frac{\pi}{4}\)
Question
Quelle est la mesure principale de
\((\vec{BD} ;\vec{BA})\)?
Solution
\((\vec{CA} ;\vec{CB})+(\vec{CB} ;\vec{CD})=\frac{\pi}{2}\)
\(\iff \frac{\pi}{3}+(\vec{CB} ;\vec{CD})=\frac{\pi}{2}\)
\(\iff (\vec{CB} ;\vec{CD})=\frac{\pi}{2}-\frac{\pi}{3}\)
\(\iff (\vec{CB} ;\vec{CD})=\frac{3\pi}{6}-\frac{2\pi}{6}=\frac{\pi}{6}\)
\((\vec{CB} ;\vec{CD})+(\vec{DC} ;\vec{DB})+(\vec{BD} ;\vec{BC})=\pi\)
CBD est un triangle isocèle :
\(\iff \frac{\pi}{6}+2(\vec{BD} ;\vec{BC})=\pi\)
\(\iff 2(\vec{BD} ;\vec{BC})=\frac{5\pi}{6}\)
\(\iff (\vec{BD} ;\vec{BC})=\frac{5\pi}{12}\)
\((\vec{BD} ;\vec{BA})=\frac{5\pi}{12}+\frac{\pi}{3}\)
\(\iff(\vec{BD} ;\vec{BA})=\frac{5\pi}{12}+\frac{4\pi}{12}\)
\(\iff(\vec{BD} ;\vec{BA})=\frac{5\pi}{12}+\frac{4\pi}{12}\)
\(\iff(\vec{BD} ;\vec{BA})=\frac{9\pi}{12}=\frac{3\pi}{4}\)
Question
2.a.Quelle est la mesure principale de \((\vec{BD} ;\vec{BE})\)?
Solution
\((\vec{BD} ;\vec{BE})\)
=\((\vec{BD} ;\vec{BA})\)+\((\vec{BA} ;\vec{BE})\)
=\(\frac{3\pi}{4}\)+\(\frac{\pi}{4}\)
=\(\frac{4\pi}{4}\)=\(\pi\)
Question
b.Que pouvez-vous en conclure ?
Solution
Les points E, B et D sont donc alignés.