Exercice : Coordonnées Polaires

Question

Le plan est reporté au repère orthonormé \((O;\vec{i};\vec{j})\) tel que (\(\vec{i},\vec{j}\))=\(\frac{π}{2}\) (2π)

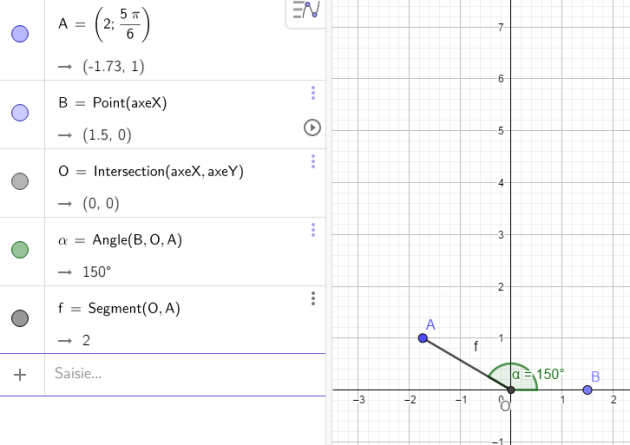
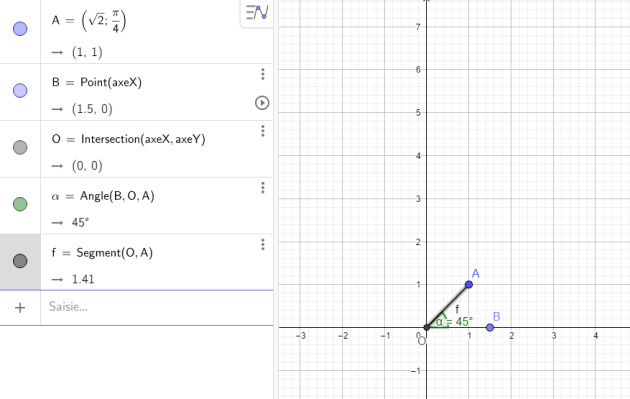
1. Donner les coordonnées cartésiennes de \(A(2 ; \frac{5π}{6})\) et B(\(\sqrt{2}\); \(\frac{π}{4}\)).

Indice

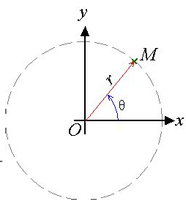
M\((r ;\theta)\)

\(M(r \times cos(\theta) , r \times sin(\theta))\)

  • Pour définir un point P ou un vecteur u en coordonnées cartésiennes validez P = (1, 0) ou u = (0, 5).

  • Pour définir un point Q ou un vecteur v en coordonnées polaires, validez Q =\( (1; \pi)\) ou v = \((5;\frac{\pi}{2})\).

Solution

\(A(2 \times cos(\frac{5π}{6}) , 2 \times sin(\frac{5π}{6}))\)

\(A(2 \times (-cos(\frac{π}{6})) , 2 \times sin(\frac{π}{6}))\)

\(A(2 \times (-\frac{\sqrt{3}}{2}) , 2 \times \frac{1}{2})\)

\(A(-\sqrt{3}, 1)\)

\(B(\sqrt{2} \times cos(\frac{π}{4}) ,\sqrt{2} \times sin(\frac{π}{4}) )\)

\(B(\sqrt{2} \times \frac{\sqrt{2}}{2},\sqrt{2} \times \frac{\sqrt{2}}{2} )\)

\(B(1,1 )\)

Question

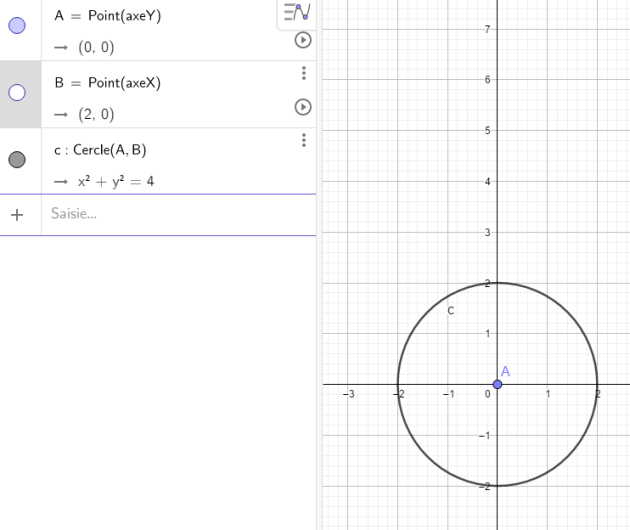
2. Dessiner l'ensemble des points M de coordonnées polaires (r ; θ) tels que :

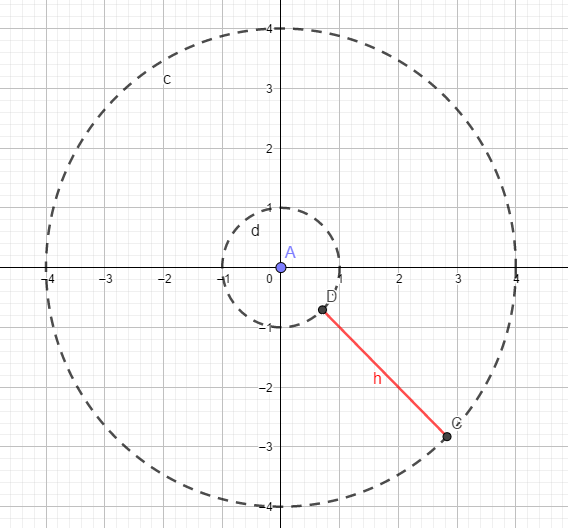
a. r=2 ; θ ϵ[0;2π ]

Solution

Question

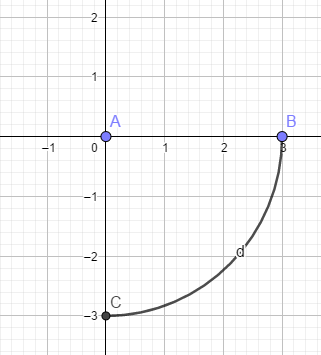
b. r=3 ; θ ϵ [\(\frac{-π}{2}\) ;0]

Solution

Question

c)r ϵ [1;4] ; \(θ =-\frac{π}{4}\)

Solution

Question

d) rϵ ]0;+∞ [; θ = π

Solution

Tout le demi-axe horizontal correspondant aux abscisses négatives sauf le point d'origine du repère.

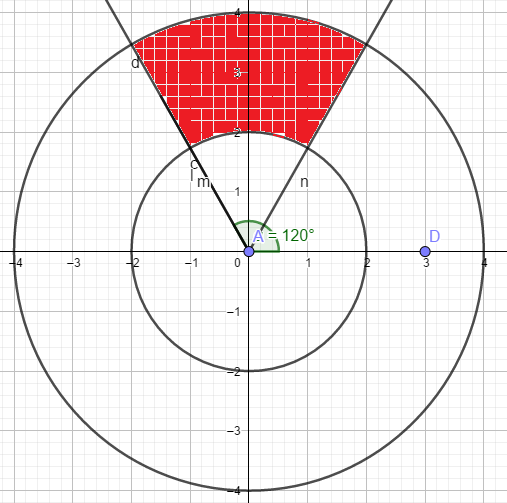
Question

e) r ϵ [2;4] ; θ ϵ [\(\frac{π}{3};\frac{2π}{3}\)]

Solution