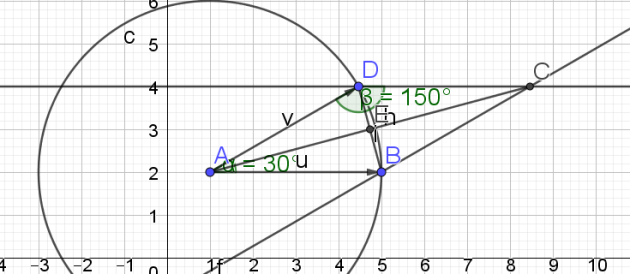
Exercice : Radians
On considère un losange ABCD tel que la mesure principale de l'angle orienté
\(\left(\overrightarrow{AB},\overrightarrow{AD}\right)\) soit \(\dfrac{\pi}{6}.\)
Question
1. Faire une figure.
Question
2. Démontrer que la somme
\(\left(\overrightarrow{DA},\overrightarrow{DC}\right)+\left(\overrightarrow{AB},\overrightarrow{AD}\right)\)
équivaut à \(\pi,\) en temps que mesure d'angle orienté.
Solution
La somme des angles d'un triangle vaut \(\pi\)
\(\left(\overrightarrow{DA},\overrightarrow{DB}\right)+\left(\overrightarrow{AB},\overrightarrow{AD}\right)+\left(\overrightarrow{BD},\overrightarrow{BA}\right)=\pi\)
Le triangle ADB est isocèle en A donc :
\(\left(\overrightarrow{DA},\overrightarrow{DB}\right)=\left(\overrightarrow{BD},\overrightarrow{BA}\right)\)
\(\iff 2\left(\overrightarrow{DA},\overrightarrow{DB}\right)+\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\pi\)
\(\left(\overrightarrow{DA},\overrightarrow{DC}\right)=2\left(\overrightarrow{DA},\overrightarrow{DB}\right)\)
donc \(\left(\overrightarrow{DA},\overrightarrow{DC}\right)+\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\pi\)
Question
3. En déduire la mesure principale de l'angle orienté \(\left(\overrightarrow{DA},\overrightarrow{DC}\right)\)
puis celle de l'angle orienté \(\left(\overrightarrow{DA},\overrightarrow{DB}\right).\)
Solution
\(\left(\overrightarrow{DA},\overrightarrow{DC}\right)+\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\pi\)
donc
\(\left(\overrightarrow{DA},\overrightarrow{DC}\right)=\pi-\left(\overrightarrow{AB},\overrightarrow{AD}\right)\)
\(\iff \left(\overrightarrow{DA},\overrightarrow{DC}\right)=\pi-\frac{\pi}{6}\)
\(iff \left(\overrightarrow{DA},\overrightarrow{DC}\right)=\frac{6\pi}{6}-\frac{\pi}{6}\)
\(iff \left(\overrightarrow{DA},\overrightarrow{DC}\right)=\frac{5\pi}{6}\)
\(\left(\overrightarrow{DA},\overrightarrow{DB}\right)=\frac{1}{2}\left(\overrightarrow{DA},\overrightarrow{DC}\right)=\frac{1}{2}\times \frac{5\pi}{6}= \frac{5\pi}{12}\)
Question
4. On note a la longueur commune aux côtés du losange ABCD.
Exprimer en fonction de a les longueurs respectives des diagonales AC et BD du losange ABCD.
Solution
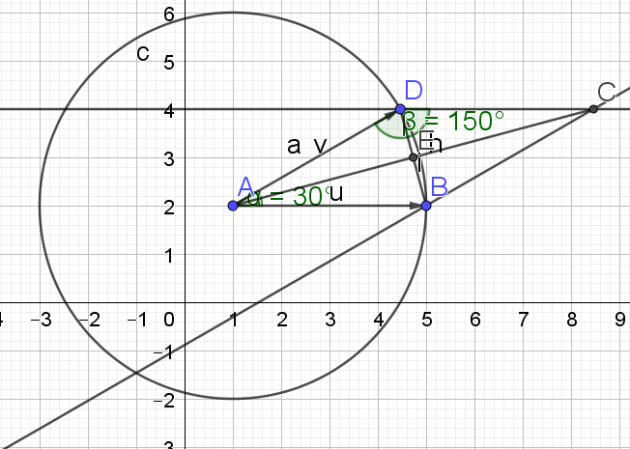
\(\cos(\frac{\frac{\pi}{6}}{2})=\frac{AE}{AD}\)
\(\iff \cos(\frac{\pi}{12})=\frac{AE}{a}\)
\(\iff AE=a\cos(\frac{\pi}{12})\)
\(\iff AC=2a\cos(\frac{\pi}{12})\)
\(\sin(\frac{\frac{\pi}{6}}{2})=\frac{DE}{AD}\)
\(\iff \sin(\frac{\pi}{12})=\frac{DE}{a}\)
\(\iff DE=a\sin(\frac{\pi}{12})\)
\(\iff BD=2a\sin(\frac{\pi}{12})\)