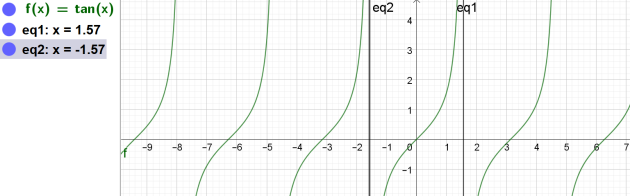
Exercice : Tangente
On appelle tangente d'un angle \(\alpha\) le réel défini par \(tan\alpha=\frac{\sin\alpha}{cos\alpha}\).
\(tan\alpha\) n'est définie que si \(cos\alpha\neq 0\)
Question
1.Quelles sont les valeurs de \(\alpha\) pour lesquelles la fonction tan n'est pas définie ?
Solution
\(cos\alpha=0\)
\(\iff \begin{cases}\alpha=-\pi+2k\pi\\\alpha=\pi+2k\pi \end{cases}\) \(k\in\mathbb{Z}\)
Question
2. Calculer \(tan 0\).
Solution
\(tan 0=\frac{sin 0}{cos 0}=\frac{0}{1}=0\)
Question
3. Calculer \(tan\frac{\pi}{4}\).
Solution
\(tan\frac{\pi}{4}=\frac{sin \frac{\pi}{4}}{cos \frac{\pi}{4}}\)
\(\iff tan\frac{\pi}{4}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}\)
\(\iff tan\frac{\pi}{4}=1\)
Question
4. Calculer \(tan\frac{\pi}{6}\).
Solution
\(tan\frac{\pi}{6}=\frac{sin \frac{\pi}{6}}{cos \frac{\pi}{6}}\)
\(\iff tan\frac{\pi}{6}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}\)
\(\iff tan\frac{\pi}{6}=\frac{1}{2} \times \frac{2}{\sqrt{3}}\)
\(\iff tan\frac{\pi}{6}=\frac{1}{\sqrt{3}}\)
\(\iff tan\frac{\pi}{6}=\frac{1}{\sqrt{3}}\)
\(\iff tan\frac{\pi}{6}=\frac{\sqrt{3}}{\sqrt{3}^2}\)
\(\iff tan\frac{\pi}{6}=\frac{\sqrt{3}}{3}\)
Question
5. Calculer \(tan\frac{\pi}{3}\).
Solution
\(tan\frac{\pi}{3}=\frac{sin \frac{\pi}{3}}{cos \frac{\pi}{3}}\)
\(\iff tan\frac{\pi}{3}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\)
\(\iff tan\frac{\pi}{3}=\frac{\frac{\sqrt{3}}{2}}{2} \times \frac{2}{1}\)
\(\iff tan\frac{\pi}{3}=\sqrt{3}\)
Question
6. Prouver que tan est \(\pi\)-périodique
Solution
\(tan(\pi+\alpha)=\frac{sin (\pi+\alpha)}{cos (\pi+\alpha)}\)
\(\iff tan(\pi+\alpha)=\frac{-sin (\alpha)}{-cos (\alpha)}\)
\(\iff tan(\pi+\alpha)=\frac{sin (\alpha)}{cos (\alpha)}=tan(\alpha)\)
Question
7. Quelle est sa parité de la fonction tangente ?
Solution
\(tan(-\alpha)=\frac{sin (-\alpha)}{cos (-\alpha)}\)
\(\iff tan(-\alpha)=\frac{-sin (\alpha)}{cos (\alpha)}\)
\(\iff tan(-\alpha)=-\frac{sin (\alpha)}{cos (\alpha)}\)
\(\iff tan(-\alpha)=-tan(\alpha)\)
Question
8. Justifier qu'on peut se limiter à une étude de cette fonction sur\( I =[ 0 ; \frac{\pi}{2}[\).
Solution
Comme la fonction tangente est \(\pi\)-périodique, on peut se limiter \([ -\frac{\pi}{2} ; \frac{\pi}{2}[\)
Il suffira de déplacer la courbe par translation de vecteur \(\pi \vec{i}\).
Comme la fonction tangente est impaire, on peut se limiter à \([ 0; \frac{\pi}{2}[\)
Il suffira de déplacer la courbe par symétrie centrale de centre l'origine du repère
Question
9. Tracer sa courbe représentative sur I, puis sur son ensemble de définition.