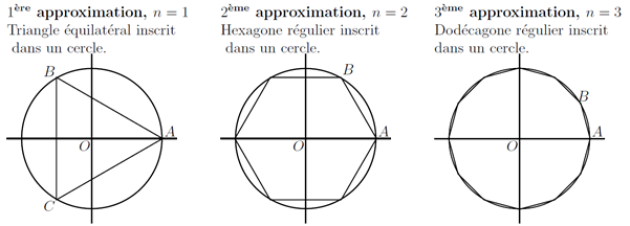
Exercice : Approximation de Pi
Dans toute la suite on considère un cercle de rayon 1 (cercle trigonométrique).
A chaque étape, pour chaque valeur de l'entier n correspondant, on note
H le milieu de [AB]
l'angle \(\alpha_n =\widehat{AOH}\),
la longueur \(L_n = AH\),
\(P_n\) le périmètre du polygone régulier.
Comme le cercle a pour rayon 1, la valeur approchée de π est alors donnée, à chaque étape, par \(π≅ \frac{P_n}{2}\) $
( En effet \(P_n\simeq 2π\))
Question
Compléter les valeurs suivantes :
Nombre de côtés | Figure 1 | Figure 2 | Figure 3 | Figure n |
|---|---|---|---|---|
\(\widehat{AOB}\) | ||||
\(\alpha_n\) | ||||
\(L_n\) | ||||
\(P_n\) | ||||
\(\pi_n\) |
Indice
Dans chacun des cas, quelle est la nature du triangle AOB et donc du triangle AOH ?.
Solution
Nombre de côtés | Figure 1 | Figure 2 | Figure 3 | Figure n |
|---|---|---|---|---|
\(\widehat{AOB}\) | \(\frac{2\pi}{3}\) | \(\frac{2\pi}{6}=\frac{\pi}{3}\) | \(\frac{2\pi}{12}=\frac{\pi}{6}\) | \(\frac{2\pi}{3 \times 2^{n-1}}\) |
\(\alpha_n\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{12}\) | \(\frac{\pi}{3 \times 2^{n-1}}\) |
\(L_n\) | \(sin(\frac{\pi}{3})\) | \(sin(\frac{\pi}{6})\) | \(sin(\frac{\pi}{12})\) | \(sin(\frac{\pi}{3 \times 2^{n-1}})\) |
\(P_n\) | \(2 \times sin(\frac{\pi}{3}) \times 3=6\times \frac{\sqrt{3}}{2}=3\sqrt{3}\) | \(2 \times sin(\frac{\pi}{6}) \times 3 \times 2=12\times \frac{1}{2}=6\) | \(2 \times sin(\frac{\pi}{12}) \times 3 \times 2^2=24sin(\frac{\pi}{12})\) | \(2 \times sin(\frac{\pi}{3 \times 2^{n-1}}) \times 3 \times 2^{n-1}\) |
\(\pi_n\) | \(3\sqrt{3}\) | 6 | \(12sin(\frac{\pi}{12})\) | \(sin(\frac{\pi}{3 \times 2^{n-1}}) \times 3 \times 2^{n-1}\) |
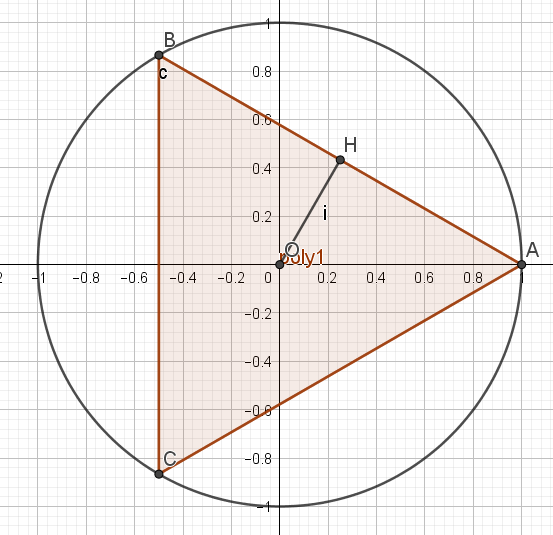
\(n=1\mapsto \text{ Nombre de côtés :} 3 \times 2^{1-1}=3\)
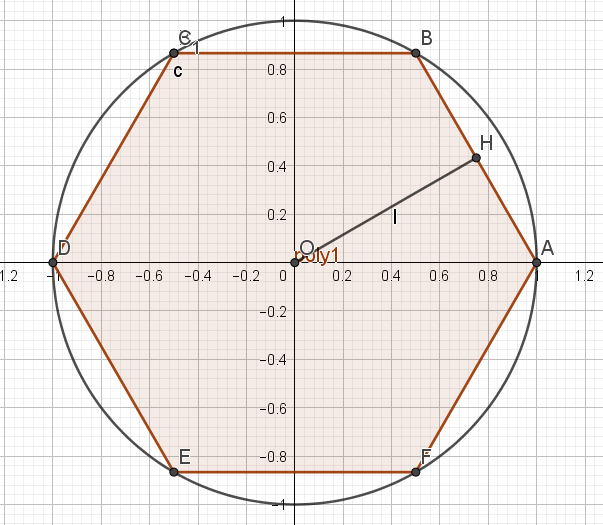
\(n=2\mapsto \text{ Nombre de côtés :} 3 \times 2^{2-1}=3 \times 2 =6\)
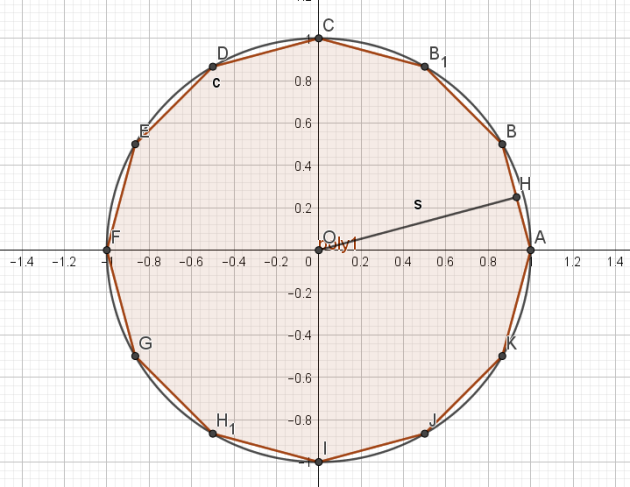
\(n=3\mapsto \text{ Nombre de côtés :} 3 \times 2^{3-1}=3 \times 4 =12\)