Exercice : Devoir Maison Equations Trigonométriques
Cherchez toutes les mesures d'angle \(x\in \mathbb{R}\) telles que :
Question
\(cos(x)=-\frac{\sqrt{3}}{2}\)
Solution
Dans l'ensemble des mesures principales (]\(-\pi ;\pi\)]),
les solutions sont
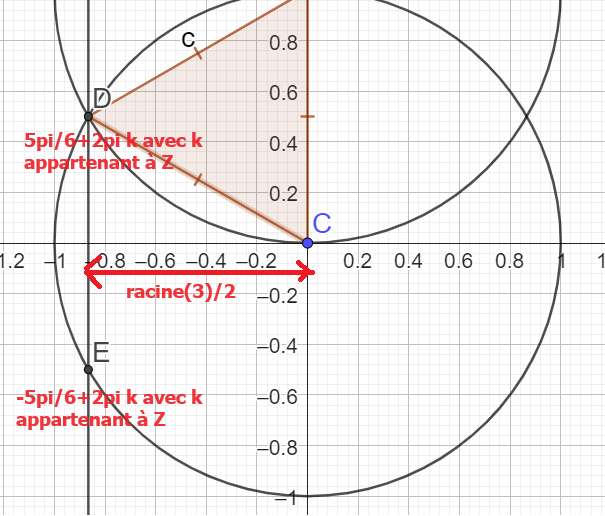
S={\(-\frac{5\pi}{6} ;\frac{5\pi}{6}\)}
et dans \(\mathbb{R}\), les solutions sont :
S={\(-\frac{5\pi}{6}+2\pi k ;\frac{5\pi}{6}+2\pi k\)}
avec \(k \in \mathbb{Z}\)
Question
2. \(2sin^2(x)-sin(x)=1\)
Solution
\(2sin^2(x)-sin(x)=1\)
\(\iff 2sin^2(x)-sin(x)-1=0\)
On effectue le changement de variable :
\(X=sin(x)\)
Pour tout \(x \in \mathbb{R}\) : \(X \in [-1 ;1]\) car le sinus d'un angle est toujours compris dans l'intervalle [-1 ;1]
\(\mapsto 2X^2-X-1=0\)
\(\begin{cases}a=2\\b=-1\\c=-1\end{cases}\)
\(\Delta=b^2-4ac\)
\(\Rightarrow \Delta=(-1)^2-4\times (2) \times (-1)\)
\(\iff \Delta=1+8\)
\(\iff \Delta=9\)
Comme \(\Delta>0\), on en déduit que l'équation \(2X^2-X-1=0\) admet deux solutions :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-(-1)-\sqrt{9}}{2 \times 2}\\X_2=\frac{-(-1)+\sqrt{9}}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{1-3}{4}\\X_2=\frac{1+3}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2}{4}\\X_2=\frac{4}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-1}{2}\\X_2=1\end{cases}\)
\(\iff \begin{cases}sin(x_1)=\frac{-1}{2}\\sin(x_2)=1\end{cases}\)
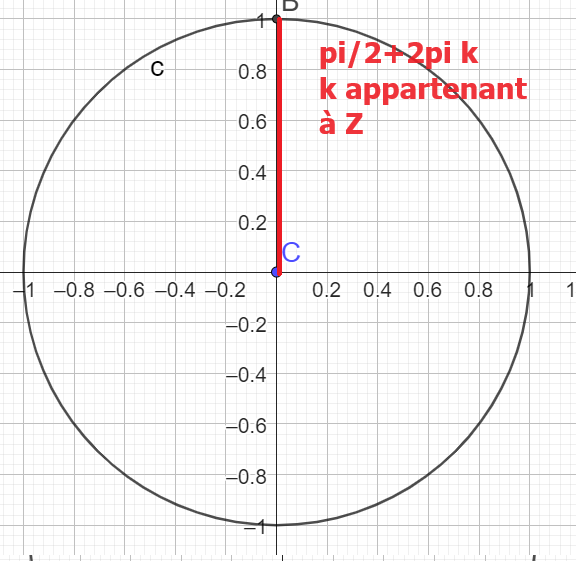
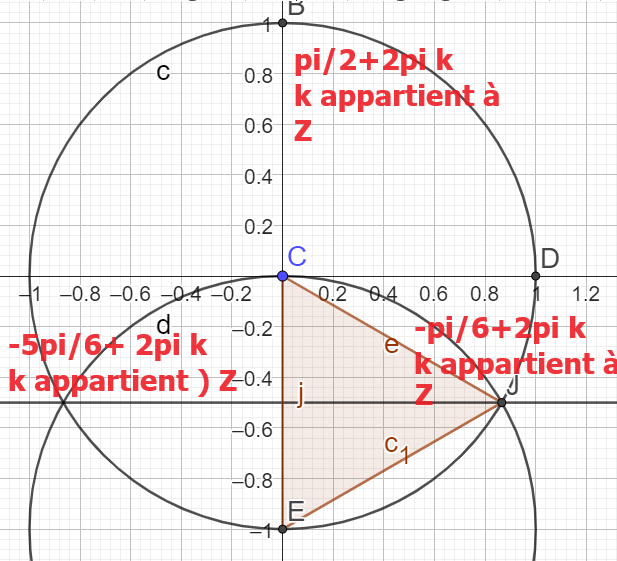
\(\Rightarrow S=\{-\frac{\pi}{6}+2\pi k;-\frac{5\pi}{6}+2\pi k ;\frac{\pi}{2}+2\pi k \}\)
avec \(k \in \mathbb{Z}\)
Question
3. \(cos^2(x)-2cos(x)+1=0\)
Solution
\(cos^2(x)-2cos(x)+1=0\)
On effectue le changement de variable :
\(X=cos(x)\)
Pour tout \(x \in \mathbb{R}\) : \(X \in [-1 ;1]\) car le cosinus d'un angle est toujours compris dans l'intervalle [-1 ;1]
\(\mapsto X^2-2X+1=0\)
\(\begin{cases}a=1\\b=-2\\c=1\end{cases}\)
\(\Delta=b^2-4ac\)
\(\Rightarrow \Delta=(-2)^2-4\times 1\times 1\)
\(\iff \Delta=4-4\)
\(\iff \Delta=0\)
Comme \(\Delta=0\), on en déduit que l'équation \(X^2-2X+1=0\) admet une solution unique :
\(X_0=cos(x_0)=1\)
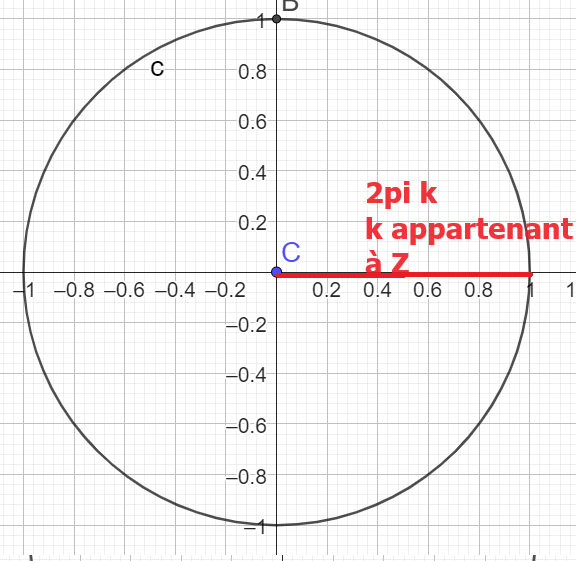
\(\Rightarrow S=\{0+2\pi k\}=\{2\pi k\}\)
avec \(k \in \mathbb{Z}\)
Question
4. \(-cos^2(y)-3sin(y)+3=0\)
Solution
\(-cos^2(y)-3sin(y)+3=0\)
On utilise la relation \(cos^2(y)+sin^2(y)=1\) pour tout \(y \in \mathbb{R}\)
donc \(cos^2(y)=1-sin^2(y)\) pour tout \(y \in \mathbb{R}\)
\(\Rightarrow -(1-sin^2(y))-3sin(y)+3=0\)
\(\iff -1+sin^2(y)-3sin(y)+3=0\)
\(\iff sin^2(y)-3sin(y)+2=0\)
On effectue le changement de variable :
\(Y=sin(y)\)
Pour tout \(y \in \mathbb{R}\) : \(Y \in [-1 ;1]\) car le sinus d'un angle est toujours compris dans l'intervalle [-1 ;1]
\(\mapsto Y^2-3X+2=0\)
\(\begin{cases}a=1\\b=-3\\c=2\end{cases}\)
\(\Delta=b^2-4ac\)
\(\Rightarrow \Delta=(-3)^2-4\times 1\times 2\)
\(\iff \Delta=9-8\)
\(\iff \Delta=1\)
Comme \(\Delta>0\), on en déduit que l'équation \(X^2-3X+2=0\) admet deux solutions :
\(\begin{cases}Y_1=\frac{-b-\sqrt{\Delta}}{2a}\\Y_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{-(-3)-\sqrt{1}}{2 \times 1}\\Y_2=\frac{-(-3)+\sqrt{1}}{2 \times 1}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{3-1}{2}\\Y_2=\frac{3+1}{2}\end{cases}\)
\(\iff \begin{cases}Y_1=\frac{2}{2}\\Y_2=\frac{4}{2}\end{cases}\)
\(\iff \begin{cases}Y_1=1\\Y_2=2\end{cases}\)
\(\iff \begin{cases}sin(y_1)=1\\sin(y_2)=2\end{cases}\)
L'équation \(sin(y_2)=2\) n'admet pas de solution d'après ce qu'on a déjà écrit car
\(Y\in [-1 ;1]\)
\(\Rightarrow S=\{\frac{\pi}{2}+2\pi k\}\)
avec \(k \in \mathbb{Z}\)