Exercice : DM Trigonométrie 2022
Exercice 1
Question
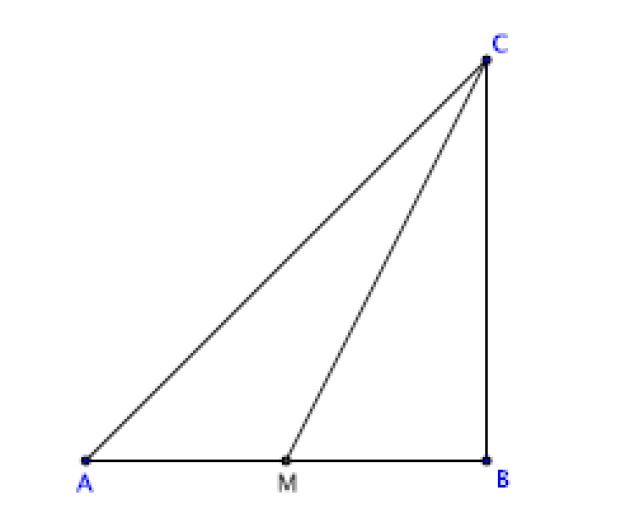
1.a. Les angles \(\widehat{ACM}\) et \(\widehat{BCM}\) ont-ils la même mesure ?
Calculer la mesure de chacun de ces deux angles, à 0,1 degré près.
Solution
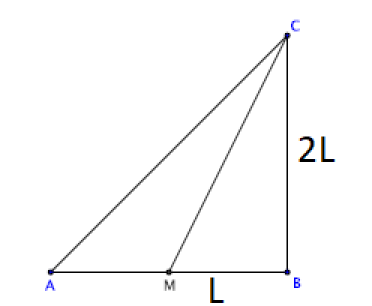
Dans le triangle MBC rectangle en B :
\(tan(\widehat{BCM})=\frac{\text{côté opposé}}{\text{côté adjacent}}=\frac{BM}{BC}\)
\(\iff tan(\widehat{BCM})=\frac{L}{2L}=\frac{1}{2}\)
\(\iff \widehat{BCM}=Arctan(\frac{1}{2})\simeq 26,6°\)
\(\widehat{BCA}+\widehat{BAC}+\widehat{CBA}=\pi\)
Le triangle ABC est rectangle et isocèle de sommet principal B
donc :
\(\begin{cases}\widehat{CBA}=\frac{\pi}{2}\\\widehat{BAC}=\widehat{BCA}\end{cases}\)
\(\widehat{BCA}+\widehat{BAC}+\widehat{CBA}=\pi\)
\(\iff 2\widehat{BCA}+\frac{\pi}{2}=\pi\)
\(\iff 2\widehat{BCA}=\pi-\frac{\pi}{2}\)
\(\iff 2\widehat{BCA}=\frac{\pi}{2}\)
\(\iff \widehat{BCA}=\frac{\pi}{4}\)
\(\widehat{BCA}=\widehat{BCM}+\widehat{ACM}\)
\(\iff 45° \simeq 26,6°+\widehat{ACM}\)
\(\iff \widehat{ACM} \simeq 45°- 26,6° \simeq 18,4°\)
Les deux angles \(\widehat{BCM}\) et \(\widehat{ACM}\) ne sont donc pas égaux.
Question
2. Les deux triangles ACM et BCM ont-ils la même aire ?
Exprimer les aires de ces deux triangles en fonction de la longueur \(L\).
Solution
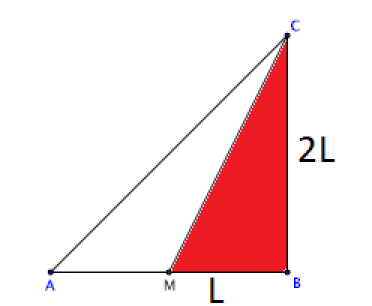
Calcul de l'aire du triangle BCM :
\(Aire=\frac{base \times hauteur}{2}=\frac{BM \times BC}{2}\)
\(\iff Aire=\frac{L \times 2L}{2}\)
\(\iff Aire=L^2\)
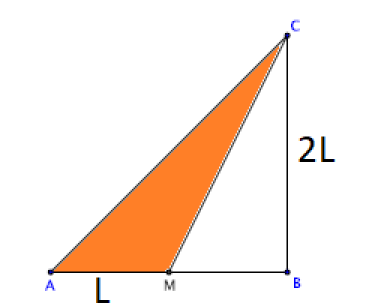
Calcul de l'aire du triangle ACM :
\(Aire=\frac{base \times hauteur}{2}=\frac{AM \times BC}{2}\)
\(\iff Aire=\frac{L \times 2L}{2}\)
\(\iff Aire=L^2\)
Les aires des deux triangles ACM et BCM sont donc égaux.
Exercice 2
.
Question
Déterminer l'ensemble de tous les nombres réels \(x\) tels que
\(cos (x) = - \frac{\sqrt{2}}{2}\) (Equation 1)
Solution
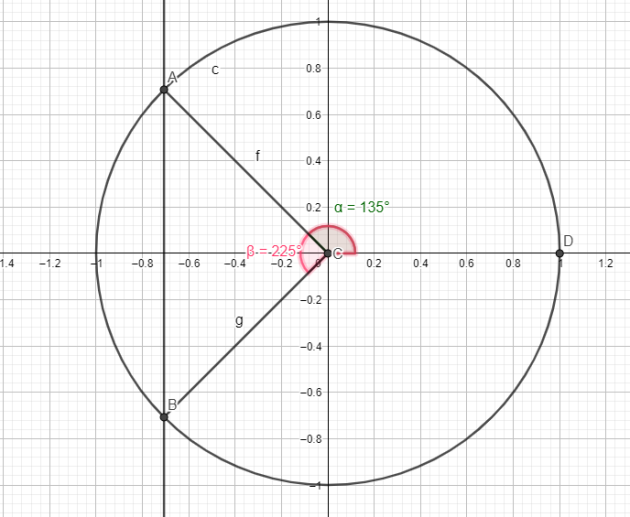
\(\begin{cases}x=\frac{\pi}{2}+\frac{\pi}{4}+2k\pi \\x=\pi+\frac{\pi}{4}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{2\pi}{4}+\frac{\pi}{4}+2k\pi\\x=\frac{4\pi}{4}+\frac{\pi}{4}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
Question
2. Donner, sous forme exacte, toutes les solutions de l'équation (1) qui appartiennent à l'intervalle \([-\pi; 2\pi]\).
Solution
\(\begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\color{magenta}{\text{1ère solution :}}\)
\(- \pi \le \frac{3\pi}{4}+2k\pi \le 2 \pi\)
\(\iff - \pi - \frac{3\pi}{4} \le 2k\pi \le 2 \pi -\frac{3\pi}{4}\)
\(\iff - \frac{4\pi}{4} - \frac{3\pi}{4} \le 2k\pi \le \frac{8\pi}{4} -\frac{3\pi}{4}\)
\(\iff - \frac{7\pi}{4} \le 2k\pi \le \frac{5\pi}{4}\)
\(\iff - \frac{7}{4} \le 2k \le \frac{5}{4}\)
\(\iff - \frac{7}{8} \le k \le \frac{5}{8}\)
\(\iff -1< k <1\)
Donc uniquement pour k=0 : \(\frac{3\pi}{4}\)
\(\color{magenta}{\text{2ème solution :}}\)
\(- \pi \le \frac{5\pi}{4}+2k\pi \le 2 \pi\)
\(\iff - \pi - \frac{5\pi}{4} \le 2k\pi \le 2 \pi -\frac{5\pi}{4}\)
\(\iff - \frac{4\pi}{4} - \frac{5\pi}{4} \le 2k\pi \le \frac{8\pi}{4} -\frac{5\pi}{4}\)
\(\iff - \frac{9\pi}{4} \le 2k\pi \le \frac{3\pi}{4}\)
\(\iff - \frac{9}{4} \le 2k \le \frac{3}{4}\)
\(\iff - \frac{9}{8} \le k \le \frac{3}{8}\)
\(\iff -2< k <1\)
Donc pour k=0 : \(\frac{5\pi}{4}\)
et pour k=-1 : \(\frac{5\pi}{4}-2\pi=\frac{5\pi}{4}-\frac{8\pi}{4}=-\frac{3\pi}{4}\)
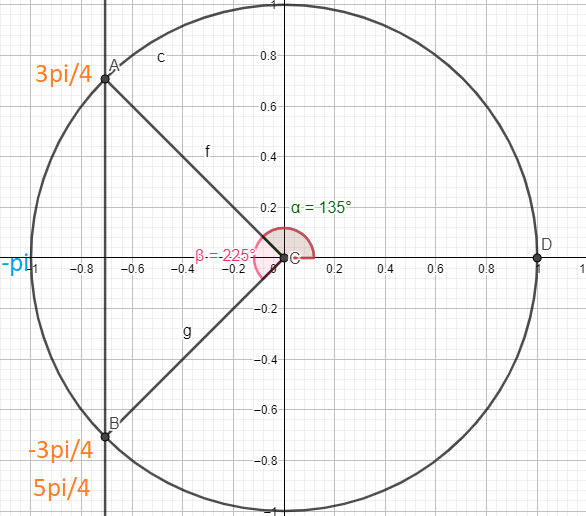
Les solutions de l'équation (1) qui appartiennent à l'intervalle \([-\pi; 2\pi]\)
sont donc : S={\(\frac{-3\pi}{4}\);\(\frac{3\pi}{4}\) ;\(\frac{5\pi}{4}\)}
Exercice 3
Résoudre dans \(\mathbb{R}\) les équations suivantes :
Question
1.\(\sin(3x)=0.5\)
Solution
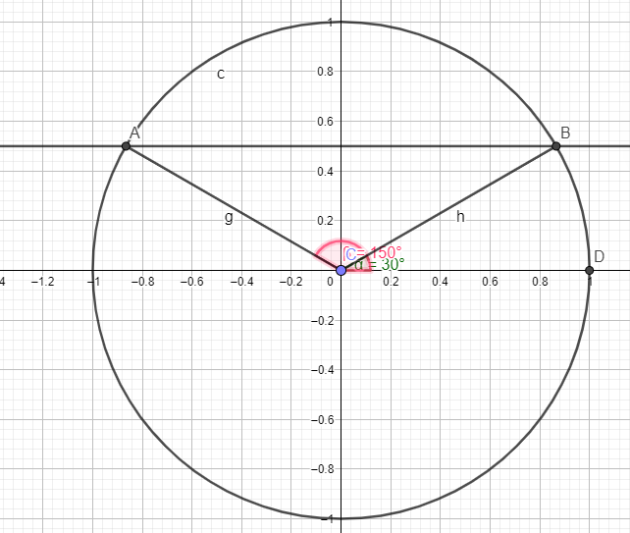
\(\begin{cases}3x=\frac{\pi}{6}+2k\pi\\3x=\pi - \frac{\pi}{6}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}3x=\frac{\pi}{6}+2k\pi\\3x=\frac{6\pi}{6}- \frac{\pi}{6}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}3x=\frac{\pi}{6}+2k\pi\\3x=\frac{5\pi}{6}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{18}+2k\frac{\pi}{3}\\x=\frac{5\pi}{18}+2k\frac{\pi}{3} \end{cases}\) \(k \in \mathbb{Z}\)
Question
2.\(\sin(4x)=\frac{\sqrt{3}}{2}\)
Solution
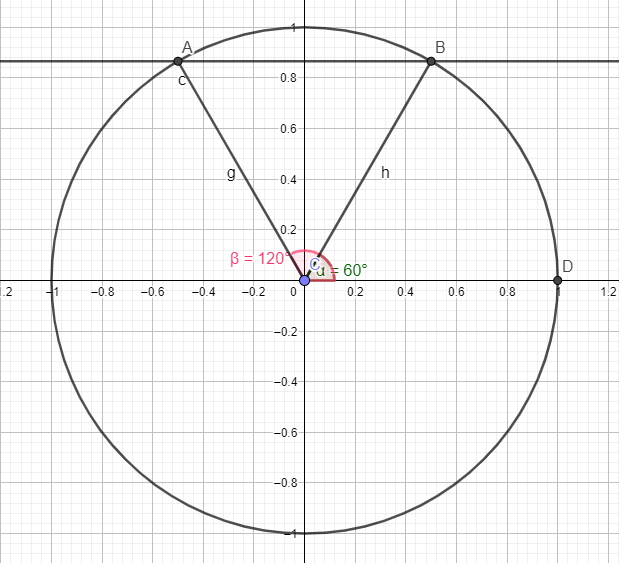
\(\begin{cases}4x=\frac{\pi}{3}+2k\pi\\4x=\pi - \frac{\pi}{3}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}4x=\frac{\pi}{3}+2k\pi\\4x=\frac{3\pi}{3}- \frac{\pi}{3}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}4x=\frac{\pi}{3}+2k\pi\\4x=\frac{2\pi}{3}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{12}+\frac{2k\pi}{4}\\x=\frac{2\pi}{12}+\frac{2k\pi}{4} \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{12}+\frac{k\pi}{2}\\x=\frac{\pi}{6}+\frac{k\pi}{2} \end{cases}\) \(k \in \mathbb{Z}\)
Question
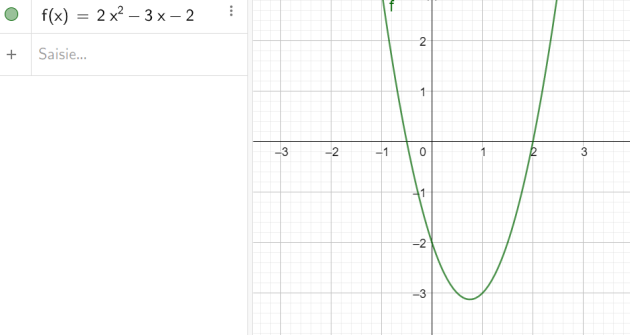
3.\(2\cos^{2}x-3cosx-2=0\)
Solution
En faisant le changement de variable :
\(X=\cos x\)
\(\iff 2X^{2}-3X-2=0\)
a=2,b=-3,c=-2
\(\Delta=b^2-4ac=(-3)^2-4\times 2 \times (-2)\)
\(\iff \Delta=9+16=25\)
Comme \(\Delta>0\), l'équation \(2X^{2}-3X-2=0\)
admet deux solutions qui sont :
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b-\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-(-3)-\sqrt{25}}{2 \times 2}\\X_2=\frac{-(-3)+\sqrt{25}}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{3-5}{4}\\X_2=\frac{3+5}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2}{4}\\X_2=\frac{8}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-1}{2}\\X_2=2\end{cases}\)
\(X_1=\frac{-1}{2}\)
\(\iff \cos(x_1)=\frac{-1}{2}\)
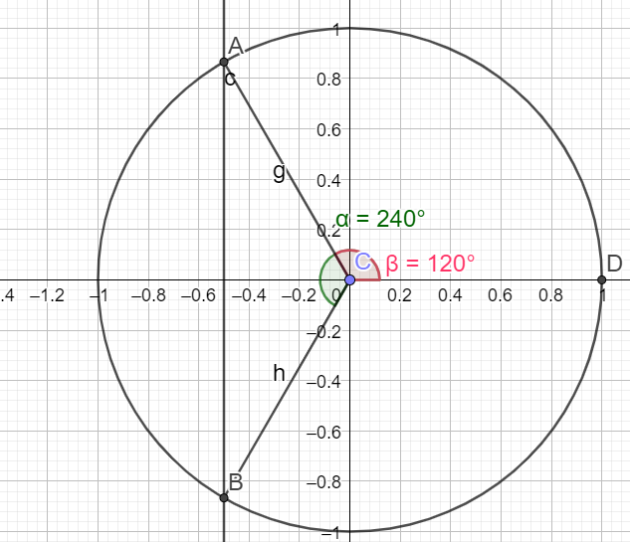
\(\begin{cases}x=\pi-\frac{\pi}{3}+2k\pi\\x=\pi + \frac{\pi}{3}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{3\pi}{3}-\frac{\pi}{3}+2k\pi\\x=\frac{3\pi}{3} + \frac{\pi}{3}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{2\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(X_2=2\)
\(\iff \cos(x_2)=2\)
Or les valeurs de la fonction cosinus sont comprises dans l'intervalle [-1 ;1]
donc il n'y a pas de solution pour l'équation \(\cos(x_2)=2\).
Les solutions de l'équation :
\(2\cos^{2}x-3cosx-2=0\)
sont donc :
\(\begin{cases}x=\frac{2\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
Question
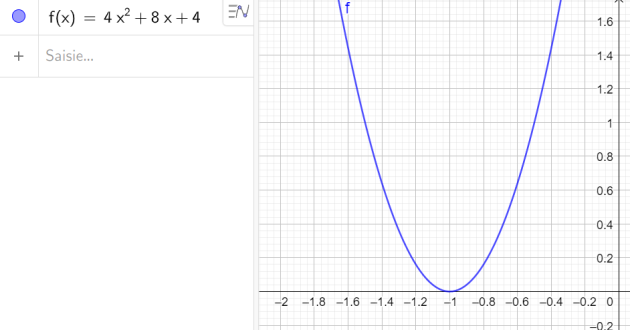
4.\(4\cos^{2}x+8cosx+4=0\)
Solution
En faisant le changement de variable :
\(X=\cos x\)
\(\iff 4X^{2}+8X+4=0\)
a=4,b=8,c=4
\(\Delta=b^2-4ac=8^2-4\times 4 \times 4\)
\(\iff \Delta=64-64=0\)
Comme \(\Delta=0\), l'équation \(4X^{2}+8X+4=0\) admet une unique solution qui est :
\(X_0=\frac{-b}{2a}=\frac{-8}{2 \times 4}=\frac{-8}{8}=-1\)
\(X_0=\cos x_0=-1\)
\(\iff x_0=\pi + 2k\pi k\in \mathbb{Z}\)
Question
5.\(\cos x=\cos(3x-\frac{\pi}{6})\)
Solution
En notant \(a=3x-\frac{\pi}{6}\)
\(\cos x=\cos(3x-\frac{\pi}{6})\)
\(\iff \cos x=\cos a\)
\(\begin{cases}x=a+2k\pi\\x=-a+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=3x-\frac{\pi}{6}+2k\pi\\x=-(3x-\frac{\pi}{6})+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=3x-\frac{\pi}{6}+2k\pi\\x=-3x+\frac{\pi}{6}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x-3x=-\frac{\pi}{6}+2k\pi\\x+3x=\frac{\pi}{6}+2k\pi \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}-2x=-\frac{\pi}{6}+2k\pi\\4x=\frac{\pi}{6}+2k\pi \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{-\frac{\pi}{6}}{-2}+\frac{2k\pi}{-2}\\x=\frac{\pi}{24}+\frac{2k\pi}{4} \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6} \times \frac{1}{-2}-k\pi\\x=\frac{\pi}{24}+\frac{k\pi}{2} \end{cases}\)
\(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{12}-k\pi\\x=\frac{\pi}{24}+\frac{k\pi}{2} \end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{12}+k\pi\\x=\frac{\pi}{24}+\frac{k\pi}{2} \end{cases}\) car si \(k \in \mathbb{Z}\) alors \(-k \in \mathbb{Z}\)
Exercice 4
1. On donne : \(\cos \left( \frac{\pi}{16} \right)=\frac{1}{2} \times \sqrt{2+\sqrt{2+\sqrt{2}}}\)
Question
a. Déterminer la valeur exacte de \(\sin \left( \frac{\pi}{16} \right)\)
Solution
\(\cos^2 \left( x \right)+\sin^2 \left( x \right)=1\)
donc
\(\cos^2 \left( \frac{\pi}{16} \right)+\sin^2 \left( \frac{\pi}{16} \right)=1\)
\(\iff (\frac{1}{2} \times \sqrt{2+\sqrt{2+\sqrt{2}}})^2+\sin^2 \left( \frac{\pi}{16} \right)=1\)
\(\iff \frac{1}{4} \times (2+\sqrt{2+\sqrt{2}})+\sin^2 \left( \frac{\pi}{16} \right)=1\)
\(\iff \sin^2 \left( \frac{\pi}{16} \right)=1-\frac{1}{4} \times (2+\sqrt{2+\sqrt{2}})\)
\(\iff \sin^2 \left( \frac{\pi}{16} \right)=\frac{4}{4}-\frac{1}{4} \times (2+\sqrt{2+\sqrt{2}})\)
\(\iff \sin^2 \left( \frac{\pi}{16} \right)=\frac{4-(2+\sqrt{2+\sqrt{2}})}{4}\)
\(\iff \sin^2 \left( \frac{\pi}{16} \right)=\frac{2-(\sqrt{2+\sqrt{2}})}{4}\)
\(\iff \begin{cases} \sin \left( \frac{\pi}{16} \right)=\frac{\sqrt{2-(\sqrt{2+\sqrt{2}})}}{2} \\ ou\sin \left( \frac{\pi}{16} \right)=-\frac{\sqrt{2-(\sqrt{2+\sqrt{2}})}}{2} \end{cases}\)
or \(\frac{\pi}{16}\in [0 ;\frac{\pi}{2}]\) donc \(\sin\frac{\pi}{16} \ge 0\)
Finalement :
\(\sin \left( \frac{\pi}{16} \right)=\frac{\sqrt{2-(\sqrt{2+\sqrt{2}})}}{2}\)
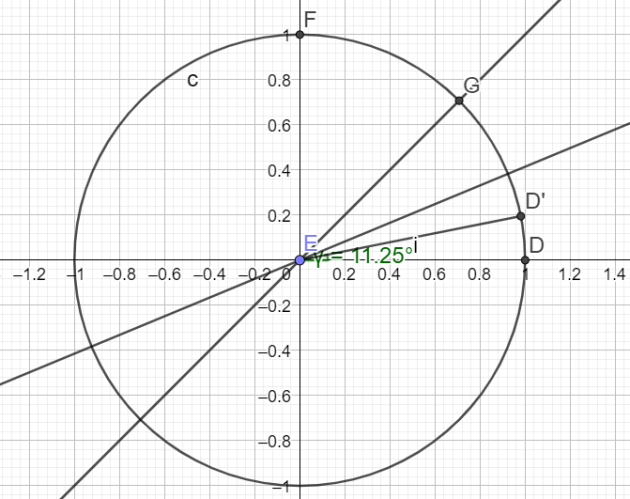
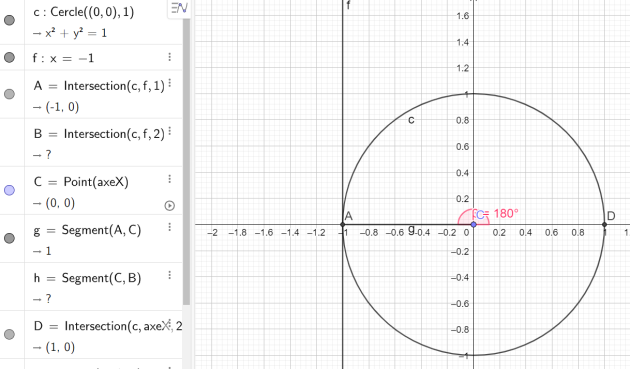
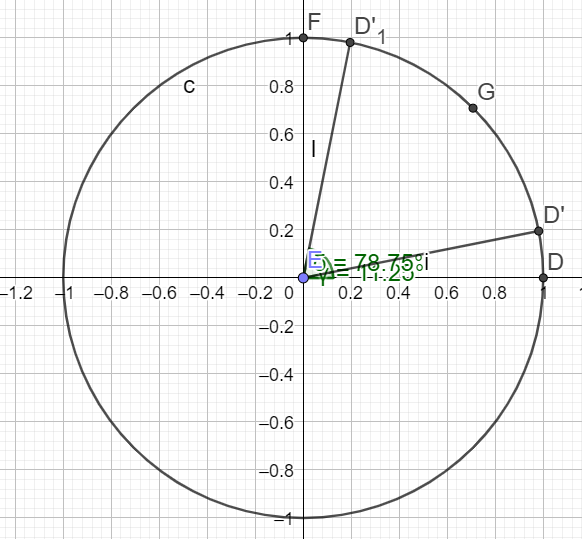
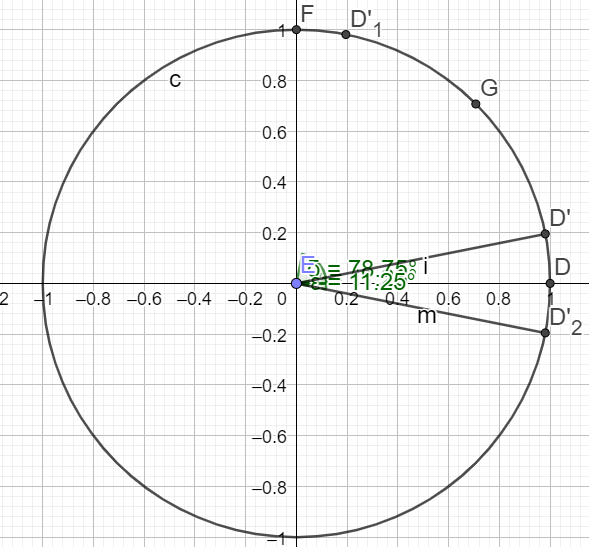
Pour construire un angle de \(\frac{\pi}{16}\),
il faut tracer trois bissectrices successives.
Question
b. En déduire la valeur exacte de \(\cos \left( \frac{7\pi}{16} \right)\) et \(\sin \left( \frac{7\pi}{16} \right)\)
Solution
\(\cos \left( \frac{7\pi}{16} \right)=\cos \left(\frac{8\pi}{16} - \frac{\pi}{16} \right)\)
\(\iff \cos \left( \frac{7\pi}{16} \right)=\cos \left(\frac{\pi}{2} - \frac{\pi}{16} \right)\)
\(\iff \cos \left( \frac{7\pi}{16} \right)=\sin \left( \frac{\pi}{16} \right)\)
\(\iff \cos \left( \frac{7\pi}{16} \right)=\frac{\sqrt{2-(\sqrt{2+\sqrt{2}})}}{2}\)
\(\sin \left( \frac{7\pi}{16} \right)=\sin \left(\frac{8\pi}{16} - \frac{\pi}{16} \right)\)
\(\iff \sin \left( \frac{7\pi}{16} \right)=\sin \left(\frac{\pi}{2} - \frac{\pi}{16} \right)\)
\(\iff \sin \left( \frac{7\pi}{16} \right)=\cos \left( \frac{\pi}{16} \right)\)
\(\iff \sin \left( \frac{7\pi}{16} \right)=\frac{1}{2} \times \sqrt{2+\sqrt{2+\sqrt{2}}}\)
Question
2. Calculer \(\sin \left( \frac{25\pi}{16} \right)\)
Solution
Déterminons la valeur principale de l'angle \(\frac{25\pi}{16}\):
\(\frac{ \frac{25\pi}{16} }{2\pi}=\frac{ \frac{25\pi}{16} }{\frac{2\pi}{1}}\)
\(\iff \frac{ \frac{25\pi}{16} }{2\pi}= \frac{25\pi}{16} \times \frac{1}{2\pi}\)
\(\iff \frac{ \frac{25\pi}{16} }{2\pi}= \frac{25\pi}{32\pi}= \frac{25}{32} \simeq 0,78\)
\(\frac{25\pi}{16}-2\pi=\frac{25\pi}{16}-\frac{32\pi}{16}\)
\(\iff \frac{25\pi}{16}-2\pi=-\frac{7\pi}{16}\)
or \(sin(-x)=sin(x)\)
donc \(\sin \left( \frac{25\pi}{16} \right)= \sin \left( -\frac{7\pi}{16} \right)= \sin \left( \frac{7\pi}{16} \right)=-\frac{1}{2} \times \sqrt{2+\sqrt{2+\sqrt{2}}}\)
Exercice 5
Simplifier au maximum les expressions suivantes :
Question
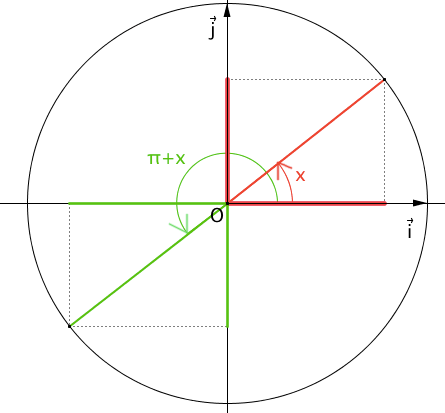
\(A = sin(x + \pi) + cos( \frac{\pi}{2}+x) + cos( \frac{\pi}{2}-x)+sin(\pi-x)\)
Solution
\(A = sin(x + \pi) + cos( \frac{\pi}{2}+x) + cos( \frac{\pi}{2}-x)+sin(\pi-x)\)
\(\iff A = -sin(x) + sin(x) + sin(x)+sin(x)\)
\(\iff A = 2sin(x)\)
\(sin(x + \pi) =-sin(x)\)
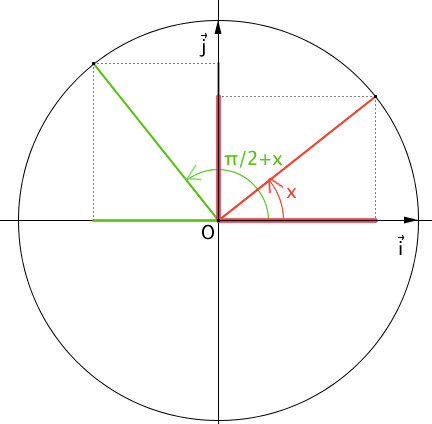
\(cos( \frac{\pi}{2}+x) =sin(x)\)
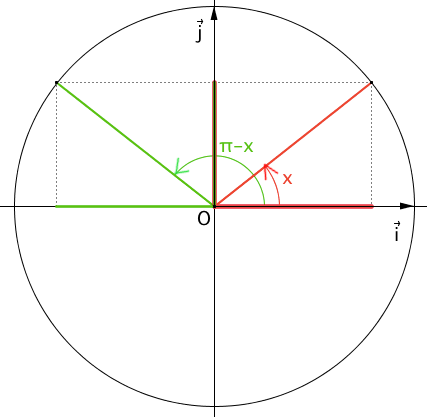
\(sin(\pi-x)=sin(x)\)
Question
\(B = sin(x - \frac{\pi}{2})+ cos(x + \pi) + cos(x-\frac{\pi}{2})+ sin(\pi-x)\)
Solution
\(B = -cos(x)-cos(x) +sin(x)+ sin(x)\)
\(B = -2cos(x)+2sin(x)=2(sin(x)-cos(x))\)
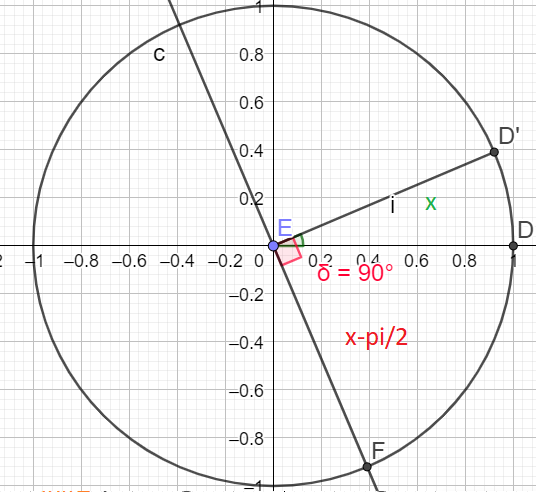
\(sin(x - \frac{\pi}{2})=-cos(x)\)
\(cos(x-\frac{\pi}{2})=sin(x)\)
\(cos(x + \pi)=-cos(x)\)

\(sin(\pi-x)=sin(x)\)

\(cos(x + \pi) =-cos(x)\)

Question
\(C= cos(x) + cos(\frac{\pi}{2}+x)+ cos (x + \pi) + cos(x + \frac{3\pi}{2})\)
Solution
\(cos(x+\frac{\pi}{2})=-sin(x)\)

\(cos(x + \frac{3\pi}{2})=sin(x)\)
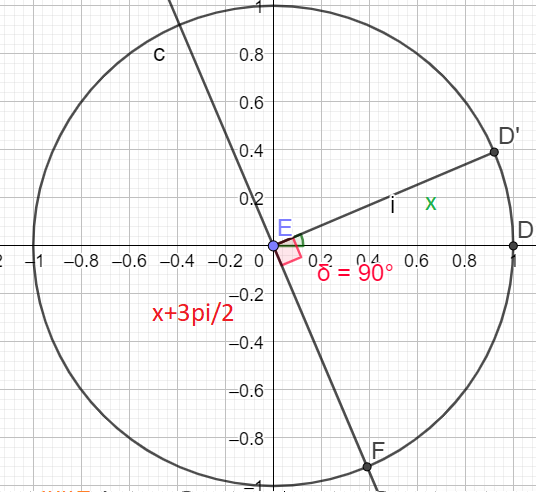
\(C= cos(x) + cos(\frac{\pi}{2}+x)+ cos (x + \pi) + cos(x + \frac{3\pi}{2})\)
\(\iff C= cos(x)-sin(x)- cos (x) + sin(x)\)
\(\iff C= 0\)
Question
\(D= sin^2x + 2cos^2x - 1\)
Solution
\(D= sin^2x + 2cos^2x - 1\)
or \(sin^2x + cos^2x=1\)
donc \(D= sin^2x + cos^2x+ cos^2x - 1\)
donc \(D= 1+ cos^2x - 1\)
donc \(D= cos^2x\)