Exercice : Devoir maison 2019
Exercice 1
Convertir en radians les mesures des angles exprimés en degrés :
Question
a. 60°
Solution
60° représente \(\frac{\pi}{3}\) radians
Question
b.150°
Solution
150° représente \(\frac{5\pi}{6}\) radians
Question
c. 10°
Solution
10° représente \(\frac{\pi}{18}\) radians
Question
d. 12°
Solution
12° représente \(\frac{\pi}{15}\) radians
Question
e. 198°
Solution
198° représente \(\frac{11\pi}{10}\) radians
Question
f. 15°
Solution
15° représente \(\frac{\pi}{12}\) radians
Exercice 2
Dans chacun des cas suivants, donner trois autres réels associés au même point sur le cercle trigonométrique :
Question
a.-\(\pi\)
Solution
-\(\pi\),\(\pi\),\(2\pi\),\(-2\pi\)
Question
b.\(\frac{3\pi}{2}\)
Solution
\(\frac{3\pi}{2}\),\(\frac{7\pi}{2},\frac{11\pi}{2}\),\(\frac{15\pi}{2}\)
Question
c.10\(\pi\)
Solution
10\(\pi\),\(12\pi\),\(14\pi\),\(-2\pi\)
Question
d.\(-\frac{\pi}{4}\)
Solution
\(-\frac{\pi}{4}\),\(-\frac{5\pi}{4}\),\(-\frac{-9\pi}{4}\),\(\frac{3\pi}{4}\)
Exercice 3
Parmi les mesures suivantes indiquer celles qui sont associées au même point que \(\frac{-\pi}{12}\) sur le cercle trigonométrique :
Question
a.\(\frac{17\pi}{12}\)
Solution
\(\frac{17\pi}{12}=\frac{24\pi}{12}-\frac{7\pi}{12}\)=\(2\pi-\frac{7\pi}{12}\)
\(\color{magenta}{Mesure principale : }\) \(-\frac{7\pi}{12}\)
\(\color{red}{\frac{17\pi}{12} \text{ n'est donc pas associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Question
b.\(\frac{-49\pi}{12}\)
Solution
\(\frac{-49\pi}{12}= \frac{-48\pi}{12}+\frac{-\pi}{12}=-4\pi+\frac{-\pi}{12}\)
\(\color{magenta}{Mesure principale : }\) \(\frac{-\pi}{12}\)
\(\color{red}{\frac{-49\pi}{12} \text{ est donc associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Question
c.\(\frac{11\pi}{12}\)
Solution
\(\frac{11\pi}{12}\)
\(\color{magenta}{Mesure principale : }\) \(\frac{11\pi}{12}\)
\(\color{red}{\frac{11\pi}{12} \text{ n'est donc pas associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Question
d.\(\frac{-241\pi}{12}\)
Solution
\(\frac{-241\pi}{12}= \frac{-240\pi}{12}+\frac{-\pi}{12}=-20\pi+\frac{-\pi}{12}\)
\(\color{magenta}{Mesure principale : }\) \(\frac{-\pi}{12}\)
\(\color{red}{\frac{-241\pi}{12} \text{ est donc associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Question
e.\(\frac{-37\pi}{12}\)
Solution
\(\frac{-37\pi}{12}= \frac{-48\pi}{12}+\frac{11\pi}{12}=-4\pi+\frac{11\pi}{12}\)\(\)
\(\color{magenta}{Mesure principale : }\) \(\frac{11\pi}{12}\)
\(\color{red}{\frac{-37\pi}{12} \text{ n'est donc pas associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Question
f.\(\frac{-313\pi}{12}\)
Solution
\(\frac{-313\pi}{12}= \frac{-312\pi}{12}+\frac{-\pi}{12}=-26\pi+\frac{-\pi}{12}\)
Mesure principale : \(\frac{-\pi}{12}\)
\(\color{magenta}{Mesure principale : }\) \(\frac{-\pi}{12}\)
\(\color{red}{\frac{-313\pi}{12} \text{ est donc associé au même point que } \frac{-\pi}{12} \text{ sur le cercle trigonométrique. }}\)
Exercice 4
.
Question
1.Sur le cercle trigonométrique, placer le point M associé à la valeur \(\frac{\pi}{6}\)
Question
2.Placer ensuite les points associés aux valeurs \(\frac{5\pi}{6}\);\(\frac{9\pi}{6}\);\(\frac{-\pi}{6}\)
Question
3.Rappeler les valeurs de \(cos \frac{\pi}{6}\) et \(sin \frac{\pi}{6}\)
Solution
\(cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}\) et \(sin \frac{\pi}{6}=\frac{1}{2 }\)
Question
4.En déduire les cosinus et sinus de \(\frac{5\pi}{6}\);\(\frac{9\pi}{6}\);\(\frac{-\pi}{6}\)
Solution
\(\begin{cases}cos\frac{5\pi}{6}=-\frac{\sqrt{3}}{2}\\sin\frac{5\pi}{6}=\frac{1}{2}\end{cases}\)
\(\begin{cases}cos(\frac{9\pi}{6})=cos(\frac{3\pi}{2})=0\\sin(\frac{9\pi}{6})=sin(\frac{3\pi}{2})=-1\end{cases}\)
\(\begin{cases}cos(\frac{-\pi}{6})=\frac{\sqrt{3}}{2}\\sin(\frac{-\pi}{6})=\frac{-1}{2}\end{cases}\)
Exercice 5
.
Question
a. Résoudre dans \(\mathbb{R}\) \(6cosx=-3\)
Solution
\(cosx=-\frac{3}{6}=-\frac{1}{2}\)
\(\iff \begin{cases}x=\frac{2\pi}{3}+2k\pi k\in \mathbb{Z}\\x=\frac{4\pi}{3}+2k\pi k\in \mathbb{Z}\end{cases}\)
Question
b. Résoudre dans ]0 ;2π] \(-\frac{\sqrt{3}}{2}+sinx=0\)
Solution
2.\(sinx=\frac{\sqrt{3}}{2}\)
\(\iff x=\frac{\pi}{3}\) ou \(x=\frac{2\pi}{3}\)
Question
c.Résoudre dans [-π;π[ \(2sin(3x)=\sqrt{2}\)
Solution
\(sin(3x)=\frac{\sqrt{2}}{2}\)
\(\iff 3x=\frac{\pi}{4}+2k\pi\) ou \(3x=\frac{3\pi}{4}+2k\pi\) \(k \in \mathbb{Z}\)
\(\iff x=\frac{\pi}{12}+\frac{2k\pi}{3}\) ou \(x=\frac{\pi}{4}+\frac{2k\pi}{3}\) \(k \in \mathbb{Z}\)
Pour k=0
\(x=\frac{\pi}{12}\) ou \(x=\frac{\pi}{4}\) \(k \in \mathbb{Z}\)
Pour k=1
\(x=\frac{\pi}{12}+\frac{2\pi}{3}\) ou \(x=\frac{\pi}{4}+\frac{2\pi}{3}\) \(k \in \mathbb{Z}\)
\(x=\frac{\pi}{12}+\frac{8\pi}{12}\) ou \(x=\frac{3\pi}{12}+\frac{8\pi}{12}\) \(k \in \mathbb{Z}\)
\(x=\frac{9\pi}{12}\)ou \(x=\frac{11\pi}{12}\)\(k \in \mathbb{Z}\)
Pour k=2
\(x=\frac{\pi}{12}+\frac{4\pi}{3} ou x=\frac{\pi}{4}+\frac{4\pi}{3} k \in \mathbb{Z}\)
\(x=\frac{\pi}{12}+\frac{16\pi}{12}\) ou \(x=\frac{3\pi}{12}+\frac{16\pi}{12}\) \(k \in \mathbb{Z}\)
\(x=\frac{17\pi}{12}\)ou \(x=\frac{19\pi}{12}\)\(k \in \mathbb{Z}\)
Ces solutions ne sont pas dans \([-\pi ,\pi[\)
Pour k=-1
\(x=\frac{\pi}{12}+\frac{-2\pi}{3}\) ou \(x=\frac{\pi}{4}+\frac{-2\pi}{3}\) \(k \in \mathbb{Z}\)
\(x=\frac{\pi}{12}+\frac{-8\pi}{12}\) ou \(x=\frac{3\pi}{12}+\frac{-8\pi}{12}\) \(k \in \mathbb{Z}\)
\(x=\frac{-7\pi}{12}\)ou \(x=\frac{-5\pi}{12}\)\(k \in \mathbb{Z}\)
Pour k=2
\(x=\frac{\pi}{12}+\frac{-4\pi}{3}\) ou \(x=\frac{\pi}{4}+\frac{-4\pi}{3}\) \(k \in \mathbb{Z}\)
\(x=\frac{\pi}{12}+\frac{-16\pi}{12}\) ou \(x=\frac{3\pi}{12}+\frac{-16\pi}{12}\) \(k \in \mathbb{Z}\)
\(x=\frac{-15\pi}{12}\)ou \(x=\frac{-13\pi}{12}\)\(k \in \mathbb{Z}\)
S={\(\frac{-7\pi}{12}\) , \(\frac{-5\pi}{12}\) ,\(\frac{\pi}{12}\),\(\frac{\pi}{4}\), \(\frac{9\pi}{12}\), \(\frac{11\pi}{12}\)}
Exercice 6
On considère un réel \(x\)\(\in\)[\(\frac{-\pi}{2}\);\(\frac{\pi}{2}\)] tel que \(sin x=\frac{\sqrt{2}-\sqrt{6}}{4}\)
Question
1.Déterminer la valeur exacte de \(cos x\)
Solution
\(sin x=\frac{\sqrt{2}-\sqrt{6}}{4}\)
\(cos^2x+sin^2x=1\)
\(\iff cos^2 x=1-(\frac{\sqrt{2}-\sqrt{6}}{4})^2=(\frac{\sqrt{2}^2-2\sqrt{2}\times\sqrt{6}+\sqrt{6}^2}{4^2})\)
\(\iff cos^2 x=1-(\frac{2-2\sqrt{12}+6}{16})\)
\(\iff cos^2 x=\frac{16}{16}-(\frac{2-2\sqrt{12}+6}{16})\)
\(\iff cos^2 x=\frac{16}{16}-(\frac{8-2\sqrt{12}}{16})\)
\(\iff cos^2 x=\frac{8+2\sqrt{12}}{16}\)
\(\iff cos^2 x=\frac{(\sqrt{2}+\sqrt{6})^2}{16}\)
\(\iff cos x=\frac{\sqrt{2}+\sqrt{6}}{4}\) ou \(cos x=-\frac{\sqrt{2}+\sqrt{6}}{4}\)
or \(x\)\(\in\)[\(\frac{-\pi}{2}\);\(\frac{\pi}{2}\) donc \(cos x\ge 0\) donc \(cos x=\frac{\sqrt{2}+\sqrt{6}}{4}\)
Question
2. On saît que \(x\in[\frac{\pi}{12} ;\frac{5\pi}{2} ;\frac{-\pi}{12} ;\frac{-5\pi}{12}]\)
Déterminer la valeur exacte de \(x\).
Solution
\(\frac{5\pi}{2} =\frac{4\pi}{2}+\frac{\pi}{2}\) donc \(cos\frac{5\pi}{2} =0\) donc cet angle est impossible
Comme le sinus est négatif \(\frac{\pi}{12} \) est impossible
Comme \(|cos x|>|sin x[\) \(x=\)\(\frac{-\pi}{12}\)
Exercice 7
On veut résoudre l'équation\( \sqrt{3}cos x=sin x\) dans \([0,2\pi[\)
Question
1. Démontrer que \(x\) est aussi solution de l'équation \(cos^2 x=\frac{1}{4}\)
Utiliser la relation \(cos^2x+sin^2x=1\)
Solution
\(cos^2x+sin^2x=1\)
\(cos^2x+(\sqrt{3}cosx)^2=1\)
\(\iff 4cos^2x=1\)
\(\iff cos^2x=\frac{1}{4}\)
Question
2.Résoudre l'équation \(cos^2 x=\frac{1}{4}\) dans \([0,2\pi[\)
Montrer que cela revient à résoudre une des deux équations
\(cos x=\frac{1}{2}\) ou \(cos x=-\frac{1}{2}\), en déduire les solutions.
Solution
\(cosx=\frac{1}{2}\) ou \(cosx=-\frac{1}{2}\)
\(\iff x=\frac{\pi}{3}\) ou \(x=\frac{2\pi}{3}\) ou \(x=\frac{4\pi}{3}\) ou \(x=\frac{5\pi}{3}\)
Question
3.Expliquer pourquoi \(cos x\) et \(sin x\) doivent avoir le même signe.
Utiliser la relation \(\sqrt{3} cos x=sinx\)
Solution
\(\sqrt{3} cos x=sinx\) donc \(\frac{sin x}{cos x}=\sqrt{3}\ge0\) donc \(cos x\) et \(sin x\) doivent avoir les mêmes signes d'après la règle des signes.
Question
4.En déduire les solutions de l'équation de départ.
Solution
Les solutions qui donnent un sinus et un cosinus de même signe sont donc
\(x=\frac{\pi}{3}\) \(x=\frac{4\pi}{3}\)
Exercice 8
Voici un schéma de la statue de la Liberté :
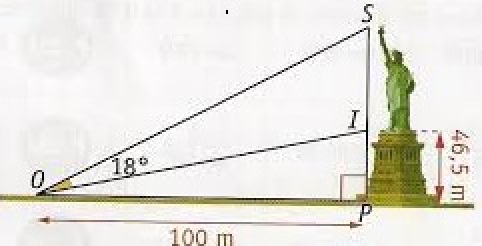
Question
Calculer une valeur approchée de la hauteur SI de la statue de la Liberté.
Solution
Dans le triangle OPI rectangle en P
\(tan(\widehat{IOP})=\frac{IP}{OP}\)
\(\iff tan(\widehat{IOP})=\frac{46,5}{100}\)
\(\iff IOP=Arctan(0,465)\simeq25\)
Dans le triangle OPS rectangle en P
\(tan(\widehat{SOP})=\frac{SP}{OP}\)
\(\iff tan(43)=\frac{SP}{100}\)
\(\iff SP=100\tan(43)\simeq93\)
La hauteur de la statue est donc de 93-46,5=46,5 mètres