Exercice : DM 2020
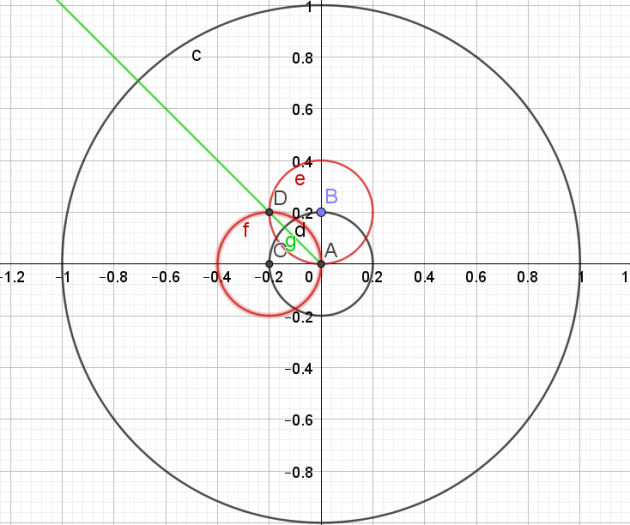
Exercice 1
Construire un cercle trigonométrique et placer les points images des nombres réels :
Question
\(a.\frac{\pi}{4}\)\(\)
Question
\(b.\frac{-\pi}{3}\)\(\)
Question
c.\(\pi\)
Question
d.\(\frac{5\pi}{6}\)
Question
e.\(\frac{-3\pi}{4}\)\(\)
Question
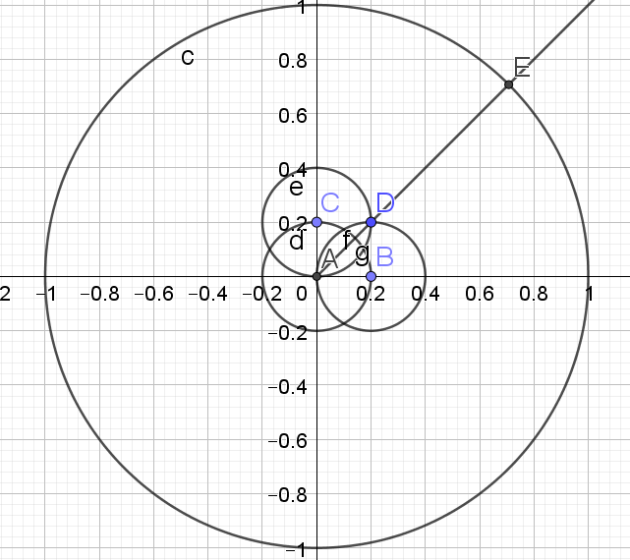
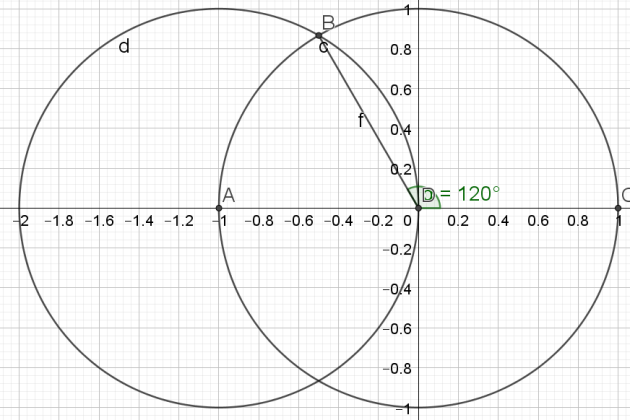
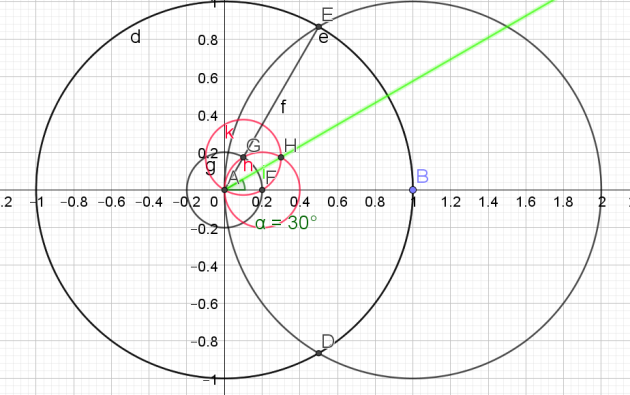
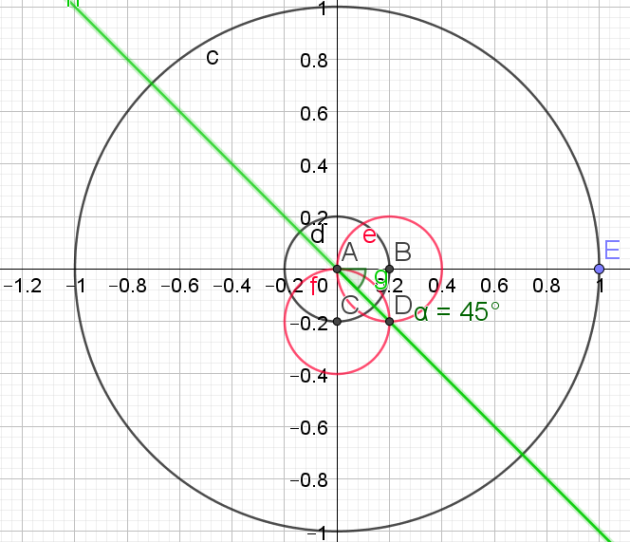
f. \(\frac{2\pi}{5}\)
Indice
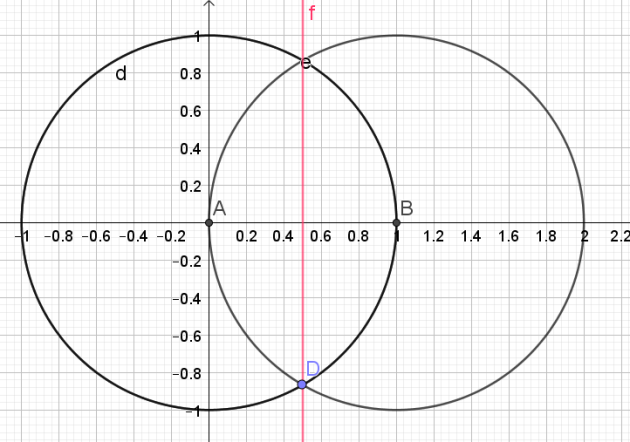
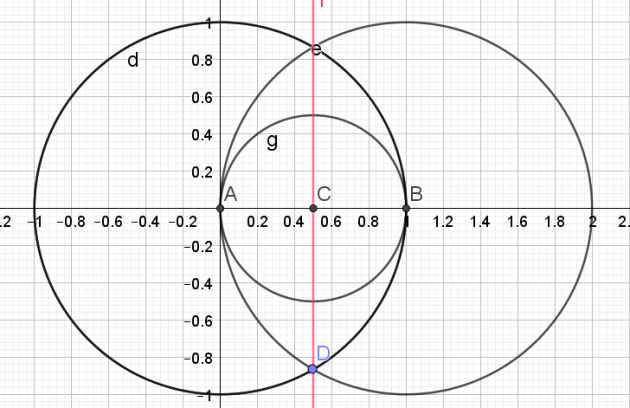
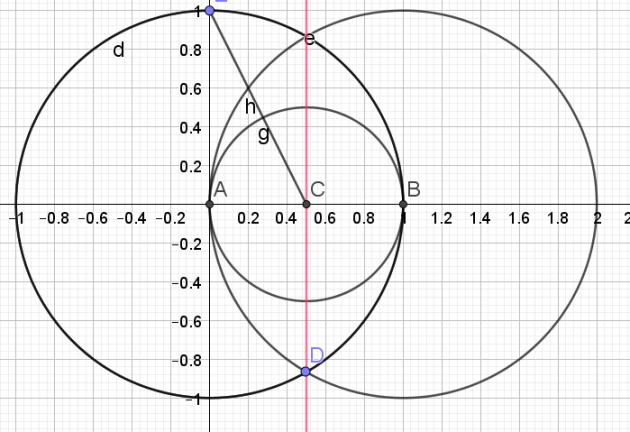
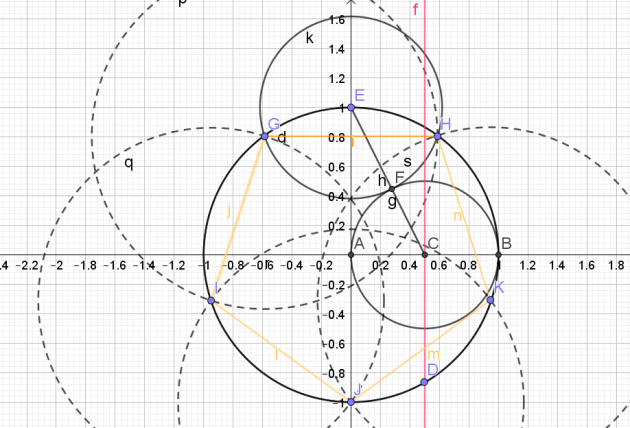
Pour construite un angle de \(\frac{2\pi}{5}\),
il faut construire le pentagone.
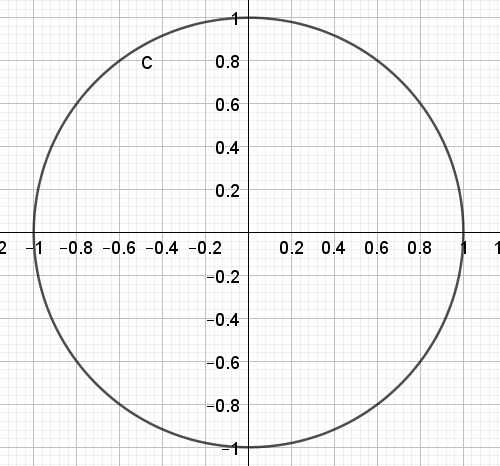
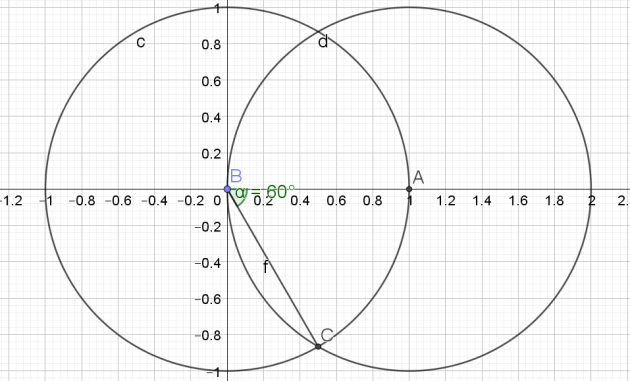
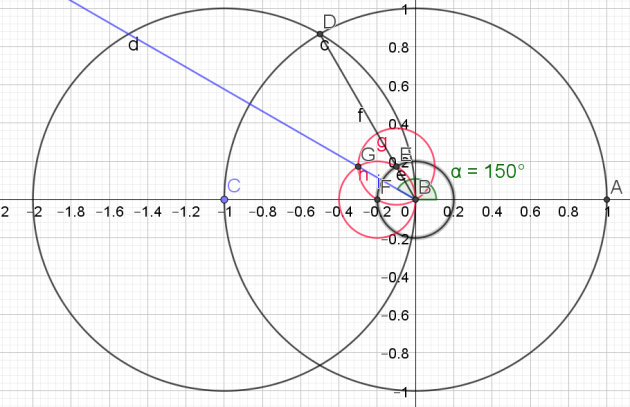
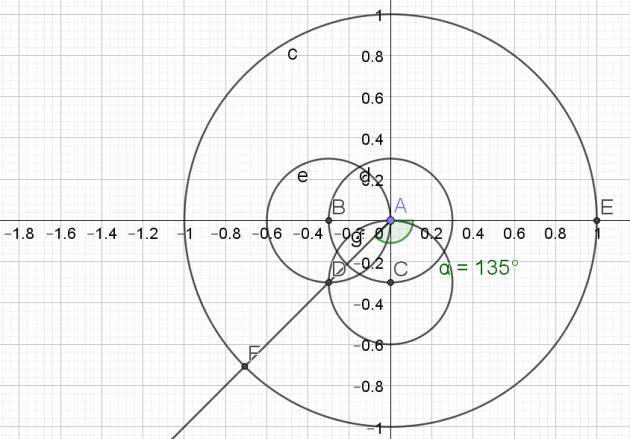
1.Tracer de la médiatrice du segment [AB] pour trouver le milieu C du segment [AB]
2.Tracer le cercle de diamètre [AB]
3.Tracer le segment [CE]
4.Soit F l'intersection du segment [CE] et du cercle de diamètre [AB]
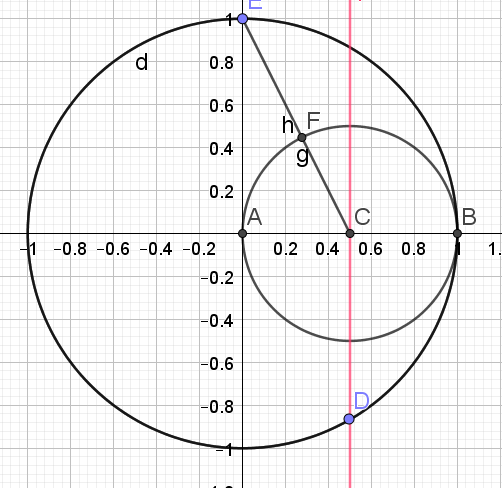
5.Tracer le cercle de centre E et de rayon [EF].
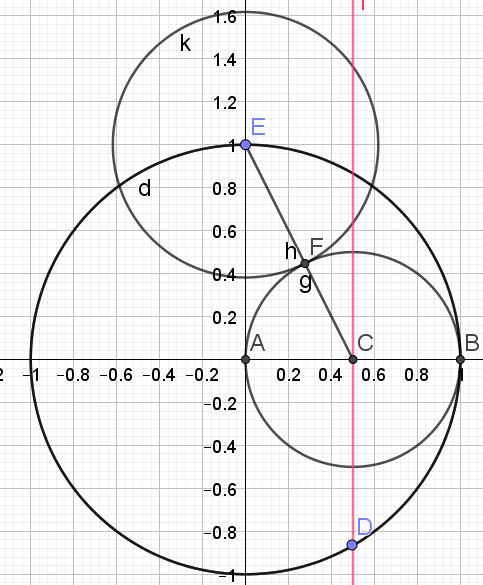
6.Soit G, les points d'intersection du cercle de centre E et de rayon [EF] et du cercle trigonométrique.
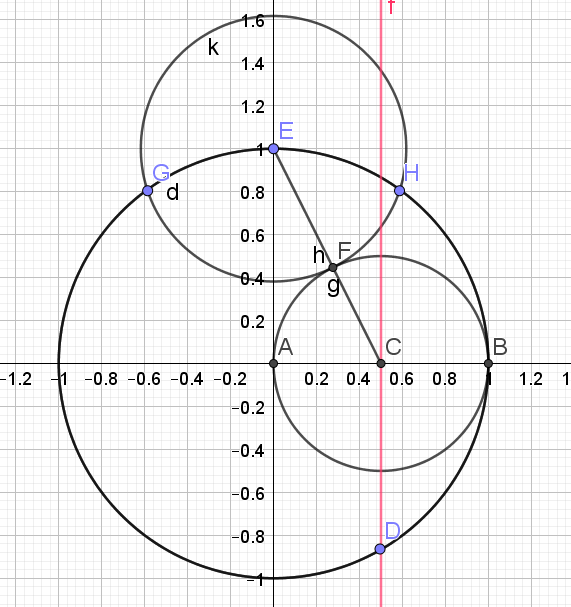
7. Tracer le segment [GH] : ce segment correspond à un des côtés du pentagone
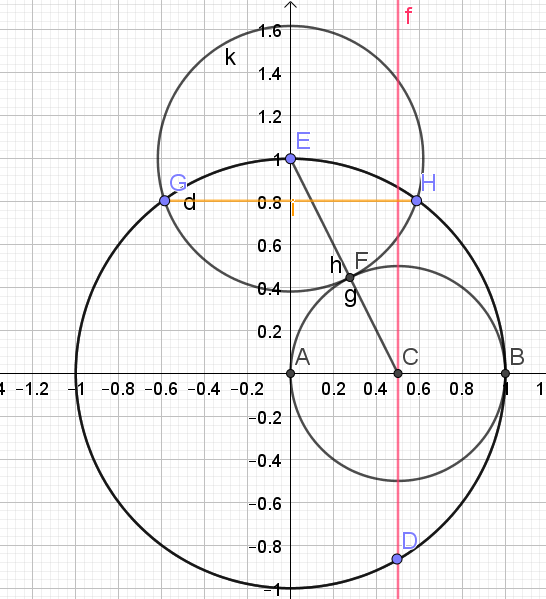
8.Reporter 5 fois cette longueur sur le cercle à l'aide du compas pour obtenir le pentagone.
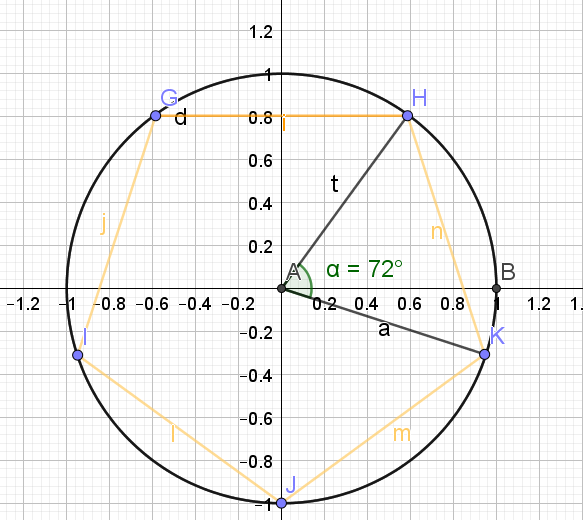
L'angle \(\widehat{KAH}\) mesure \(\frac{2\pi}{5}\)
Il suffit maintenant de reporter cet angle à partir du point B pour obtenir un angle de \(\frac{2\pi}{5}\)
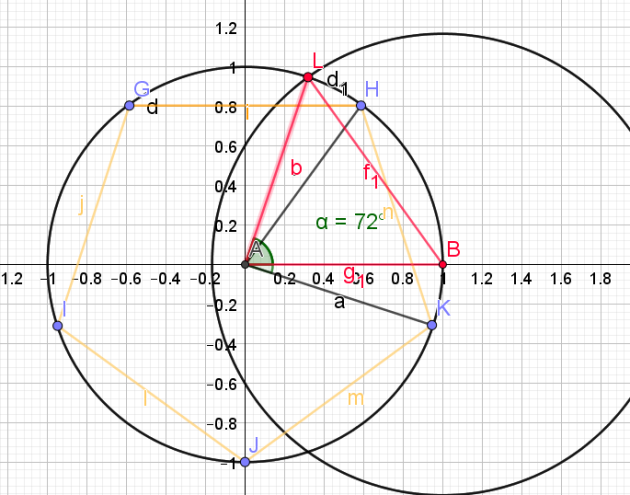
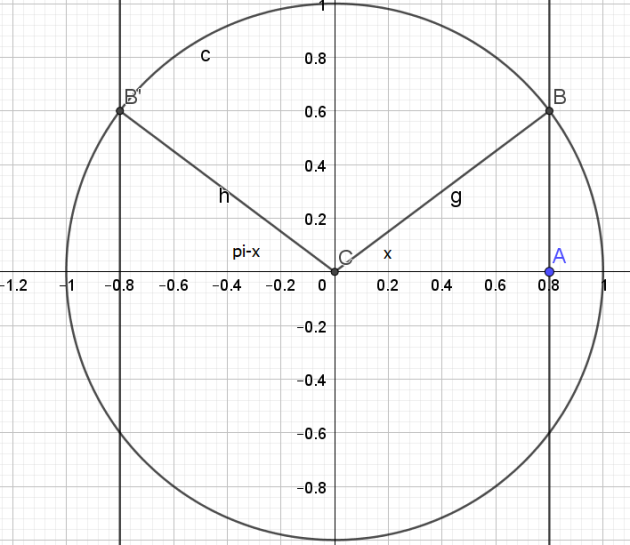
Exercice 2
.
Question
a. Donner un nombre réel positif et un nombre réel négatif ayant le même point image sur le cercle trigonométrique C que le nombre réel \(\frac{-\pi}{3}\)
Solution
Par exemple :
\(\frac{-\pi}{3}+2\pi=\frac{-\pi}{3}+\frac{6\pi}{3}=\frac{5\pi}{3}\)
\(\frac{-\pi}{3}-2\pi=\frac{-\pi}{3}-\frac{6\pi}{3}=\frac{-7\pi}{3}\)
Question
b. Donner tous les nombres réels ayant le même point image sur le cercle que le nombre réel \(\frac{2\pi}{3}\)
Solution
\(\frac{2\pi}{3}+2k\pi\) \(k\in\mathbb{Z}\)
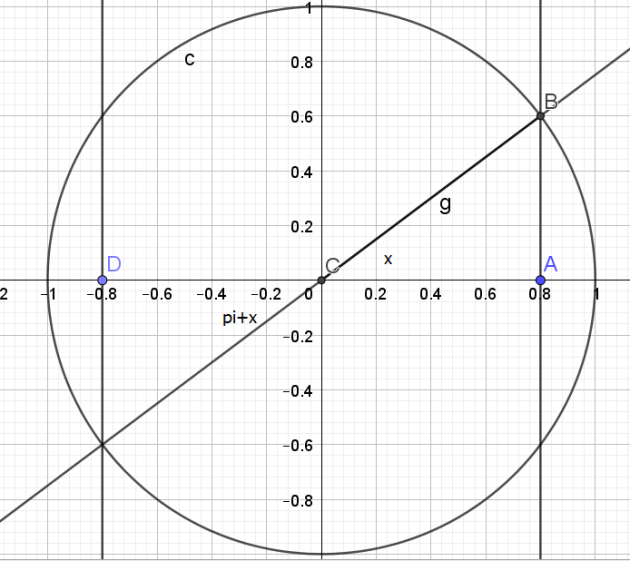
Exercice 3
Dans chaque cas, dire si les deux nombres réels ont le même point image sur un cercle trigonométrique :
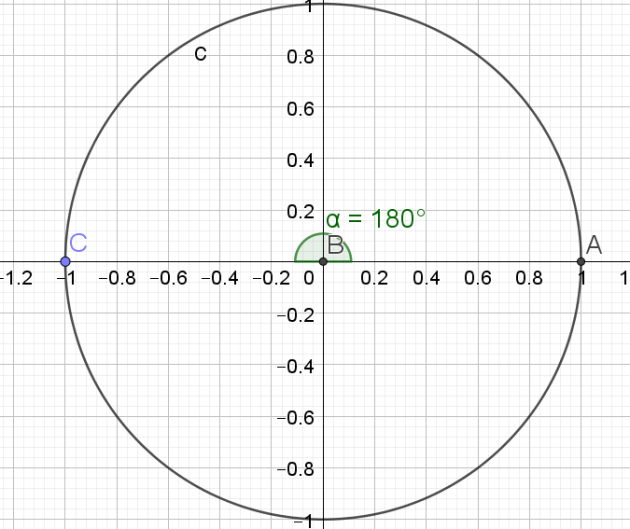
Question
a.\(\frac{\pi}{6}\) et \(\frac{13\pi}{6}\)
Indice
On pourra chercher si la différence des mesures des deux angles est un multiple de \(2\pi\)
Solution
\(\frac{13\pi}{6}-\frac{\pi}{6}=\frac{12\pi}{6}=2\pi\)
donc les deux angles sont distincts de un tour
donc les deux angles correspondent au même point sur le cercle trigonométrique.
Question
b.\(\frac{-\pi}{4}\) et \(\frac{11\pi}{4}\)
Indice
On pourra chercher si la différence des mesures des deux angles est un multiple de \(2\pi\)
Solution
\(\frac{11\pi}{4}\) -(\(\frac{-\pi}{4}\))= \(\frac{12\pi}{4}=3\pi\)
donc les deux angles sont distincts de un tour et demi
donc les deux angles ne correspondent pas au même point sur le cercle trigonométrique.
Question
c.\(\frac{-\pi}{3}\) et \(\frac{-13\pi}{3}\)
Indice
On pourra chercher si la différence des mesures des deux angles est un multiple de \(2\pi\)
Solution
\(\frac{-\pi}{3}\) - \(\frac{-13\pi}{3}\)
=\(\frac{-\pi}{3}\) + \(\frac{13\pi}{3}\)
=\(\frac{12\pi}{3}\)
\(=4\pi\)
donc les deux angles sont distincts de deux tours
donc les deux angles correspondent au même point sur le cercle trigonométrique.
Exercice 4
Déterminer dans chaque cas la mesure principale de l'angle dont une mesure est donnée :
Question
\(a .\frac{5\pi}{4}\)
Solution
\(\frac{\frac{5\pi}{4}}{2\pi}\)
\(=\frac{\frac{5\pi}{4}}{\frac{2\pi}{1}}\)
\(=\frac{5\pi}{4} \times \frac{1}{2\pi}\)
\(=\frac{5\pi}{8\pi}\)
\(=\frac{5}{8}\)
\(0\le \frac{5}{8} \le 1\)
\(\frac{5\pi}{4}-0 \times 2\pi=\frac{5\pi}{4}\notin]-\pi ;\pi]\)
\(\frac{5\pi}{4}-1 \times 2\pi=\frac{5\pi}{4}-\frac{8\pi}{4}=-\frac{3\pi}{4} \in]-\pi ;\pi]\)
La mesure principale de \(\frac{5\pi}{4}\) est donc de \(-\frac{3\pi}{4}\)
Question
\(b .\frac{-4\pi}{3}\)
Solution
\(\frac{\frac{-4\pi}{3}}{2\pi}\)
\(=\frac{\frac{-4\pi}{3}}{\frac{2\pi}{1}}\)
\(=\frac{-4\pi}{3} \times \frac{1}{2\pi}\)
\(=\frac{-4\pi}{6\pi}\)
\(=\frac{-4}{6}\)
\(=\frac{-2}{3}\)
\(-1 \le \frac{-2}{3} \le 0\)
\(\frac{-4\pi}{3}+0 \times 2\pi=\frac{-4\pi}{3}\notin]-\pi ;\pi]\)
\(\frac{-4\pi}{3}+1 \times 2\pi=\frac{-4\pi}{3}+\frac{6\pi}{3}=\frac{2\pi}{3} \in]-\pi ;\pi]\)
La mesure principale de \(\frac{-4\pi}{3}\) est donc de \(\frac{2\pi}{3}\)
Question
c.\(\frac{-10\pi}{3}\)
Solution
\(\frac{\frac{-10\pi}{3}}{2\pi}\)
\(=\frac{\frac{-10\pi}{3}}{\frac{2\pi}{1}}\)
\(=\frac{-10\pi}{3} \times \frac{1}{2\pi}\)
\(=\frac{-10\pi}{6\pi}\)
\(=\frac{-10}{6}\)
\(=\frac{-10}{6}\)
\(-3 \le \frac{-10}{6} \le -2\)
\(\frac{-10\pi}{3} +2 \times 2\pi=\frac{-10\pi}{3}+\frac{12\pi}{3}=\frac{2\pi}{3} \in]-\pi ;\pi]\)
\(\frac{-10\pi}{3} +3 \times 2\pi=\frac{-10\pi}{3}+\frac{18\pi}{3}=\frac{8\pi}{3} \notin]-\pi ;\pi]\)
La mesure principale de \(\frac{-10\pi}{3}\) est donc de \(\frac{2\pi}{3}\)
Question
d.\(135\pi\)
Solution
\(\frac{135\pi}{2\pi}\)
=\(\frac{135}{2}\)
\(67 \le \frac{135}{2} \le 68\)
\(135\pi -67 \times 2\pi=135\pi -134\pi=\pi \in]-\pi ;\pi]\)
\(135\pi -68 \times 2\pi=135\pi -136\pi=-\pi \notin]-\pi ;\pi]\)
La mesure principale de \(135\pi\) est donc de \(\pi\)
Question
e.\(\frac{185\pi}{6}\)
Solution
\(\frac{\frac{185\pi}{6}}{2\pi}\)
\(=\frac{\frac{185\pi}{6}}{\frac{2\pi}{1}}\)
=\(\frac{185\pi}{6} \times \frac{1}{2\pi}\)
=\(\frac{185\pi}{12\pi}\)
=\(\frac{185}{12}\)
\(15 \le \frac{185}{12} \le 16\)
\(\frac{185\pi}{6} -15 \times 2\pi=\frac{185\pi}{6} -\frac{180\pi}{6}=\frac{5\pi}{6} \in]-\pi ;\pi]\)
\(\frac{185\pi}{6} -16 \times 2\pi=\frac{185\pi}{6} -\frac{192\pi}{6}=\frac{-7\pi}{6} \notin]-\pi ;\pi]\)
La mesure principale de \(\frac{185\pi}{6}\) est donc de \(\frac{5\pi}{6}\)
Question
f.\(\frac{17\pi}{13}\)
Solution
\(\frac{\frac{17\pi}{13}}{2\pi}\)
\(=\frac{\frac{17\pi}{13}}{\frac{2\pi}{1}}\)
=\(\frac{17\pi}{13} \times \frac{1}{2\pi}\)
=\(\frac{17\pi}{26\pi}\)
=\(\frac{17}{26}\)
\( 0 \le \frac{17}{26} \le 1\)
\(\frac{17\pi}{13} -0 \times 2\pi=\frac{17\pi}{13} \notin]-\pi ;\pi]\)
\(\frac{17\pi}{13} -1 \times 2\pi=\frac{17\pi}{13} -\frac{26\pi}{13}=\frac{-9\pi}{13} \in ]-\pi ;\pi]\)
La mesure principale de \(\frac{17\pi}{13}\) est donc de \(\frac{-9\pi}{13}\)
Exercice 5
Calculer la valeur exacte du cosinus et du sinus de chaque nombre réel :
Question
\(a \frac{5\pi}{3}\)
Solution
\(cos(\frac{5\pi}{3})\)
\(=cos(\frac{6\pi}{3}-\frac{\pi}{3})\)
\(=cos(2\pi-\frac{\pi}{3})\)
\(=cos(-\frac{\pi}{3})\) or \(cos(-x)=cos(x)\)
\(=\frac{1}{2}\)
\(sin(\frac{5\pi}{3})\)
\(=sin(\frac{6\pi}{3}-\frac{\pi}{3})\)
\(=sin(2\pi-\frac{\pi}{3})\)
\(=sin(-\frac{\pi}{3})\) or \(sin(-x)=-sin(x)\)
\(=-\frac{\sqrt{3}}{2}\)
Question
\(b \frac{-5\pi}{6}\)
Solution
\(cos(\frac{-5\pi}{6})\)
\(=cos(\frac{-5\pi}{6}+2\pi)\)
\(=cos(\frac{-5\pi}{6}+\frac{12\pi}{6})\)
\(=cos(\frac{7\pi}{6})\)
\(=cos(\frac{6\pi}{6}+\frac{\pi}{6})\)
\(=cos(\frac{\pi}{6}+\pi)\) or \(cos(x+\pi)=-cos(x)\)
\(=-cos(\frac{\pi}{6})\)
\(=-\frac{\sqrt{3}}{2}\)
\(sin(\frac{-5\pi}{6})\)
\(=sin(\frac{-5\pi}{6}+2\pi)\)
\(=sin(\frac{-5\pi}{6}+\frac{12\pi}{6})\)
\(=sin(\frac{7\pi}{6})\)
\(=sin(\frac{6\pi}{6}+\frac{\pi}{6})\)
\(=sin(\frac{\pi}{6}+\pi)\) or \(sin(x+\pi)=-sin(x)\)
\(=-sin(\frac{\pi}{6})\)
\(=-\frac{1}{2}\)
Question
\(c.\frac{-3\pi}{4}\)
Solution
\(cos(\frac{-3\pi}{4})\)
\(=cos(\frac{-3\pi}{4}+2\pi)\)
\(=cos(\frac{-3\pi}{4}+\frac{8\pi}{4})\)
\(=cos(\frac{5\pi}{4})\)
\(=cos(\frac{4\pi}{4}+\frac{\pi}{4})\)
\(=cos(\frac{\pi}{4}+\pi)\) or \(cos(x+\pi)=-cos(x)\)
\(=-cos(\frac{\pi}{4})\)
\(=-\frac{\sqrt{2}}{2}\)
\(sin(\frac{-3\pi}{4})\)
\(=sin(\frac{-3\pi}{4}+2\pi)\)
\(=sin(\frac{-3\pi}{4}+\frac{8\pi}{4})\)
\(=sin(\frac{5\pi}{4})\)
\(=sin(\frac{4\pi}{4}+\frac{\pi}{4})\)
\(=sin(\frac{\pi}{4}+\pi)\) or \(sin(x+\pi)=-sin(x)\)
\(=-sin(\frac{\pi}{4})\)
\(=-\frac{\sqrt{2}}{2}\)
Question
\(d .\frac{13\pi}{6}\)
Solution
\(cos(\frac{13\pi}{6})\)
\(=cos(\frac{\pi}{6}+\frac{12\pi}{6})\)
\(=cos(\frac{\pi}{6}+2\pi)\)
\(=cos(\frac{\pi}{6})\)
\(=\frac{\sqrt{3}}{2}\)
\(sin(\frac{13\pi}{6})\)
\(=sin(\frac{\pi}{6}+\frac{12\pi}{6})\)
\(=sin(\frac{\pi}{6}+2\pi)\)
\(=sin(\frac{\pi}{6})\)
\(=\frac{1}{2}\)
Question
\(e.\frac{9\pi}{4}\)
Solution
\(cos(\frac{9\pi}{4})\)
\(=cos(\frac{\pi}{4}+\frac{8\pi}{4})\)
\(=cos(\frac{\pi}{4}+2\pi)\)
\(=cos(\frac{\pi}{4})\)
\(=\frac{\sqrt{2}}{2}\)
\(sin(\frac{9\pi}{4})\)
\(=sin(\frac{\pi}{4}+\frac{8\pi}{4})\)
\(=sin(\frac{\pi}{4}+2\pi)\)
\(=sin(\frac{\pi}{4})\)
\(=\frac{\sqrt{2}}{2}\)
Question
\(f .\frac{11\pi}{6}\)
Solution
\(cos(\frac{11\pi}{6})\)
\(=cos(\frac{12\pi}{6}-\frac{\pi}{6})\)
\(=cos(2\pi-\frac{\pi}{6})\)
\(=cos(-\frac{\pi}{6})\) or \(cos(-x)=cos(x)\)
\(=\frac{\sqrt{3}}{2}\)
\(sin(\frac{11\pi}{6})\)
\(=sin(\frac{12\pi}{6}-\frac{\pi}{6})\)
\(=sin(2\pi-\frac{\pi}{6})\)
\(=sin(-\frac{\pi}{6})\) or \(sin(-x)=-sin(x)\)
\(=-\frac{1}{2}\)
Question
\(g .\frac{71\pi}{3}\)
Solution
\(\frac{\frac{71\pi}{3}}{2\pi}\)
\(=\frac{\frac{71\pi}{3}}{\frac{2\pi}{1}}\)
=\(\frac{71\pi}{3} \times \frac{1}{2\pi}\)
=\(\frac{71\pi}{6\pi}\)
=\(\frac{71}{6}\)
\( 11 \le \frac{71}{6} \le 12\)
\(\frac{71\pi}{3} -11 \times 2\pi=\frac{71\pi}{3}-\frac{66\pi}{3}=\frac{5\pi}{3} \notin]-\pi ;\pi]\)
\(\frac{71\pi}{3} -12 \times 2\pi=\frac{71\pi}{3}-\frac{72\pi}{3}=\frac{-\pi}{3} \in]-\pi ;\pi]\)
La mesure principale de \(\frac{71\pi}{3}\) est donc de \(\frac{-\pi}{3}\)
\(cos(\frac{71\pi}{3})\)
\(=cos(\frac{-\pi}{3})\) or \(cos(-x)=cos(x)\)
\(=\frac{1}{2}\)
\(sin(\frac{71\pi}{3})\)
\(=sin(-\frac{\pi}{3})\)
\(=-sin(\frac{\pi}{3})\) or \(sin(-x)=-sin(x)\)
\(=-\frac{\sqrt{3}}{2}\)
Question
\(h .\frac{-5\pi}{4}\)
Solution
\(cos(\frac{-5\pi}{4})\)
\(=cos(\frac{-5\pi}{4}+2\pi)\)
\(=cos(\frac{-5\pi}{4}+\frac{8\pi}{4})\)
\(=cos(\frac{3\pi}{4})\)
\(=-\frac{\sqrt{2}}{2}\)
\(sin(\frac{-5\pi}{4})\)
\(=sin(\frac{-5\pi}{4}+2\pi)\)
\(=sin(\frac{-5\pi}{4}+\frac{8\pi}{4})\)
\(=sin(\frac{3\pi}{4})\)
\(=\frac{\sqrt{2}}{2}\)
Exercice 6
\(x\) est un nombre réel tel que :
\(cos x=\frac{4}{5}\) et \(sin(x)=\frac{3}{5}\)
A l'aide d'un cercle trigonométrique , déterminer le cosinus et le sinus
de chacun des nombres réels :
Question
a. \(-x\)\(\)
Solution
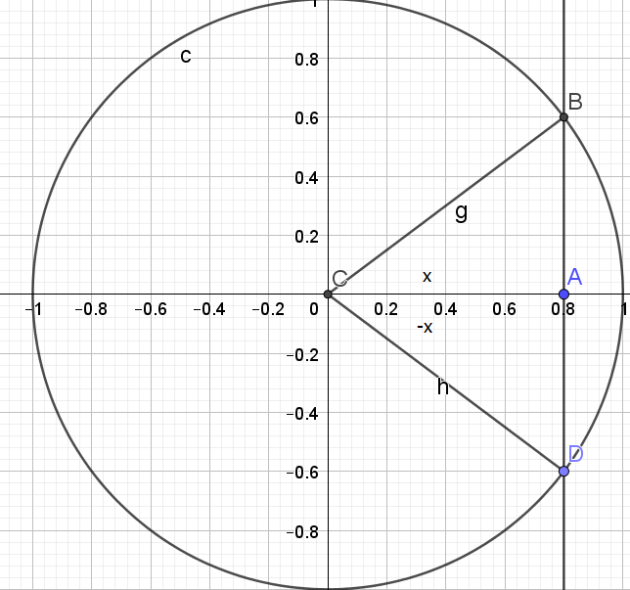
\(cos(-x)=cos(x)=\frac{4}{5}\) et \(sin(-x)=-sin(x)=-\frac{3}{5}\)
Question
b. \(\pi-x\)\(\)
Solution
\(cos(\pi-x)=-cos(x)=-\frac{4}{5}\) et \(sin(\pi-x)=sin(x)=\frac{3}{5}\)
Question
c. \(\pi+x\)
Solution
\(cos(\pi+x)=-cos(x)=-\frac{4}{5}\) et \(sin(\pi+x)=-sin(x)=-\frac{3}{5}\)
Question
d. \(\frac{\pi}{2}-x\)
Solution
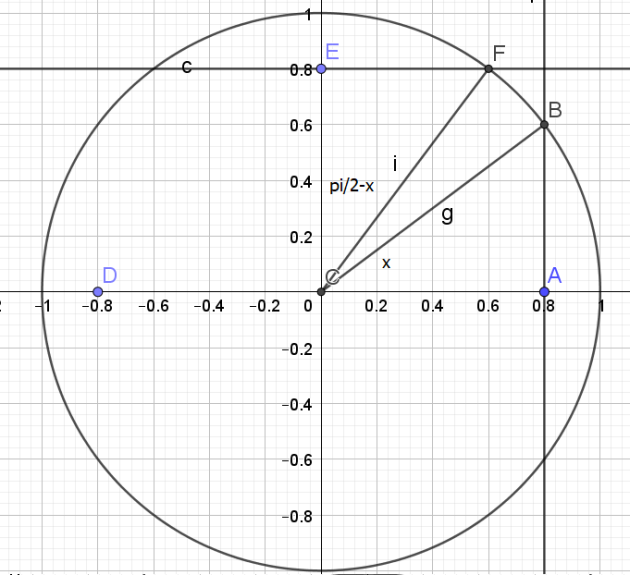
\(cos(\frac{\pi}{2}-x)=sin(x)=\frac{3}{5}\) et \(sin(\frac{\pi}{2}-x)=cos(x)=\frac{4}{5}\)
Question
e. \(\frac{\pi}{2}+x\)
Solution
\(cos(\frac{\pi}{2}+x)=-sin(x)=-\frac{3}{5}\) et \(sin(\frac{\pi}{2}+x)=cos(x)=\frac{4}{5}\)
Exercice 7
On donne \(cos(\frac{\pi}{5})=\frac{\sqrt{5}+1}{4}\)
Question
1. Calculer la valeur exacte de \(sin \frac{\pi}{5}\)
Indice
Appliquer la formule \(cos^2 x +sin^2 x=1\) et tenir compte du signe de \(sin \frac{\pi}{5}\)
Solution
\(cos^2 (\frac{\pi}{5}) +sin^2 (\frac{\pi}{5})=1\)
or \(cos(\frac{\pi}{5})=\frac{\sqrt{5}+1}{4}\)
\((\frac{\sqrt{5}+1}{4})^2 +sin^2 (\frac{\pi}{5})=1\)
\(\iff \frac{(\sqrt{5}+1)^2}{16} +sin^2 (\frac{\pi}{5})=1\)
\(\iff sin^2 (\frac{\pi}{5})=1-(\frac{(\sqrt{5}+1)^2}{16})\)
\(\iff sin^2 (\frac{\pi}{5})=1-(\frac{\sqrt{5}^2+2\sqrt{5} \times 1+1^2}{16})\)
\(\iff sin^2 (\frac{\pi}{5})=1-(\frac{5+2\sqrt{5}+1}{16})\)
\(\iff sin^2 (\frac{\pi}{5})=\frac{16}{16}-(\frac{6+2\sqrt{5}}{16})\)
\(\iff sin^2 (\frac{\pi}{5})=\frac{16-6-2\sqrt{5}}{16}\)
\(\iff sin^2 (\frac{\pi}{5})=\frac{10-2\sqrt{5}}{16}\)
\(\iff sin^2 (\frac{\pi}{5})=\frac{5-\sqrt{5}}{16}\)
or \(\frac{\pi}{5}\in [0 ;\frac{\pi}{2}]\) donc \(sin(\frac{\pi}{5})\ge0\)
\(\iff sin(\frac{\pi}{5})=\frac{\sqrt{5-\sqrt{5}}}{4}\)
2. En déduire les valeurs exactes du cosinus et du sinus de chaque nombre réel :
Question
a. \(\frac{4\pi}{5}\)
Solution
\(cos(\frac{4\pi}{5})\)
\(=cos(\frac{5\pi}{5}-\frac{\pi}{5})\)
\(=cos(\pi-\frac{\pi}{5})\) or \(cos(\pi-x)=-cos(x)\)
\(=-cos(\frac{\pi}{5})\)
\(=-\frac{\sqrt{5}+1}{4}\)
\(sin(\frac{4\pi}{5})\)
\(=sin(\frac{5\pi}{5}-\frac{\pi}{5})\)
\(=sin(\pi-\frac{\pi}{5})\) or \(sin(\pi-x)=sin(x)\)
\(=sin(\frac{\pi}{5})\)
\(=\frac{\sqrt{5-\sqrt{5}}}{4}\)
Question
b. \(\frac{-\pi}{5}\)
Solution
\(cos(\frac{-\pi}{5})\) or \(cos(-x)=cos(x)\)
\(=cos(\frac{\pi}{5})\)
\(=\frac{\sqrt{5}+1}{4}\)
\(sin(\frac{-\pi}{5})\) or \(sin(-x)=-sin(x)\)
\(=-sin(\frac{\pi}{5})\)
\(=-\frac{\sqrt{5-\sqrt{5}}}{4}\)
Question
c. \(\frac{6\pi}{5}\)
Solution
\(cos(\frac{6\pi}{5})\)
\(=cos(\frac{5\pi}{5}+\frac{\pi}{5})\)
\(=cos(\pi+\frac{\pi}{5})\) or \(cos(\pi+x)=-cos(x)\)
\(=-\frac{\sqrt{5}+1}{4}\)
\(sin(\frac{6\pi}{5})\)
\(=sin(\frac{5\pi}{5}+\frac{\pi}{5})\)
\(=sin(\pi+\frac{\pi}{5})\) or \(sin(\pi+x)=-sin(x)\)
\(=-\frac{\sqrt{5-\sqrt{5}}}{4}\)
Question
d. \(\frac{3\pi}{10}\)
Solution
\(\frac{\pi}{2}-\frac{\pi}{5}=\frac{5\pi}{10}-\frac{2\pi}{10}=\frac{3\pi}{10}\)
\(cos(\frac{3\pi}{10})\)
\(=cos(\frac{\pi}{2}-\frac{\pi}{5})\) or \(cos(\frac{\pi}{2}-x)=sin(x)\)
\(=sin(\frac{\pi}{5})\)
\(=\frac{\sqrt{5-\sqrt{5}}}{4}\)
\(sin(\frac{3\pi}{10})\)
\(=sin(\frac{\pi}{2}-\frac{\pi}{5})\) or \(sin(\frac{\pi}{2}-x)=cos(x)\)
\(=cos(\frac{\pi}{5})\)
\(=\frac{\sqrt{5}+1}{4}\)
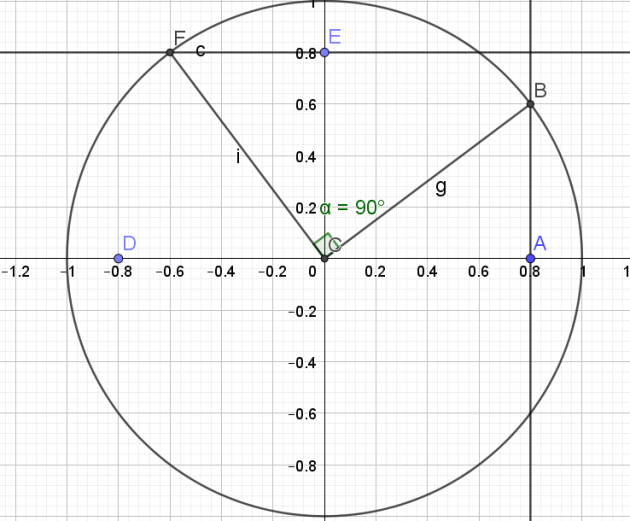
Exercice 8
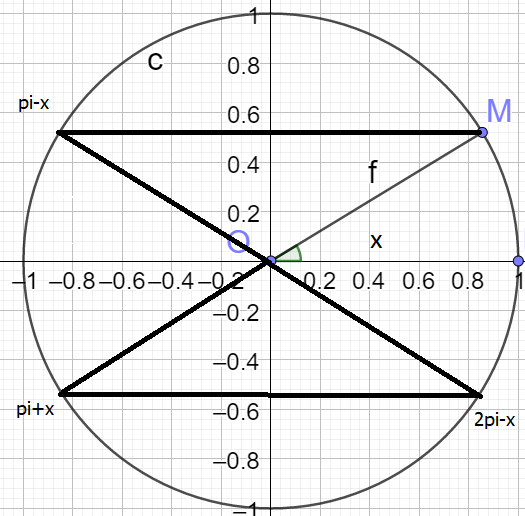
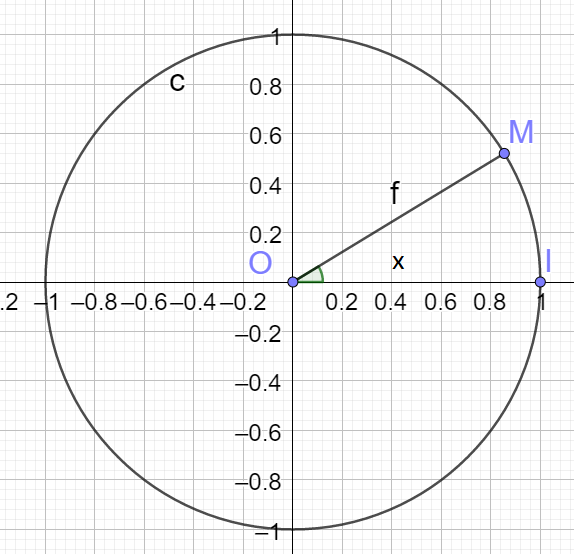
Reproduire le cercle trigonométrique C ci-contre où M est le point image d'un nombre réel \(x\).
Question
a.Placer sur C les points images des nombres réels \(\pi-x\);\(\pi+x\);\(2\pi-x\)
Question
b.Simplifier :
\(A=sin x +sin(\pi-x)+sin(\pi+x)+sin(2\pi-x)\)
Solution
\(A=sin x +sin(\pi-x)+sin(\pi+x)+sin(2\pi-x)\)
\(\begin{cases}sin(\pi-x)=sin(x)\\sin(\pi+x)=-sin(x)\\sin(2\pi-x)=-sin(x)\end{cases}\)
\(\iff A=sin x +sin(x)-sin(x)-sin(x)\)
\(\iff A=0\)
Exercice 9
.
Question
1. Placer sur un cercle trigonométrique le point M image du nombre réel \(x\)
tel que :
\(x\in[-\frac{\pi}{2} ;0]\) et \(cos x=\frac{3}{4}\)
2. Calculer la valeur exacte de :
Question
a. \(sin x\)
Solution
\(cos^2 (x) +sin^2 (x)=1\)
or \(cos(x)=\frac{3}{4}\)
\((\frac{3}{4})^2 +sin^2 (x)=1\)
\(\iff \frac{9}{16} +sin^2 (x)=1\)
\(\iff sin^2 (x)=1-\frac{9}{16}\)
\(\iff sin^2 (x)=\frac{16}{16}-\frac{9}{16}\)
\(\iff sin^2 (x)=\frac{7}{16}\)
or \(x\in [-\frac{\pi}{2} ;0]\) donc \(sin(x)\le0\)
\(\iff sin(x)=-\frac{\sqrt{7}}{4}\)
Question
b. \(cos (-x)\)
Solution
\(cos(-x)=cos(x)=\frac{3}{4}\)
Question
c. \(cos (\pi+x)\)
Solution
\(cos(\pi+x)=-cos(x)=-\frac{3}{4}\)
Question
d. \(sin (\frac{\pi}{2}-x)\)
Solution
\(sin (\frac{\pi}{2}-x)=cos(x)=\frac{3}{4}\)
Question
e. \(cos(\frac{\pi}{2}+x)\)
Solution
\(cos (\frac{\pi}{2}+x)=-sin(x)=-\frac{\sqrt{7}}{4}\)
Exercice 10
1. En s'aidant du cercle trigonométrique, résoudre dans \(]-\pi ;\pi]\),
puis dans \(\mathbb{R}\),les équations :
Question
a. \(sin(x)=\frac{-1}{2}\)
Solution
\(sin(x)=\frac{-1}{2}\)
\(sin(x)=\frac{-1}{2}=sin(\frac{\pi}{6})\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\pi-(-\frac{\pi}{6})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\pi+\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{6\pi}{6}+\frac{\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{7\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(\mathbb{R}\) sont :
\(\begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{7\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
RECHERCHE DES SOLUTIONS DANS \(]-\pi ;\pi]\) :
Pour \(k=0\) :
\(\begin{cases}x=-\frac{\pi}{6}+2 \times 0 \times \pi\\x=\frac{7\pi}{6}+2 \times 0 \times\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{6} \in]-\pi ;\pi]\\x=\frac{7\pi}{6} \notin]-\pi ;\pi]\end{cases}\)
Donc inutile de prendre des valeurs de \(k\) supérieures pour la deuxième solution.
Pour \(k=1\) :
\(x=-\frac{\pi}{6}+2 \times 1 \times \pi\)
\(\iff \begin{cases}x=-\frac{\pi}{6} +\frac{12\pi}{6}=\frac{13\pi}{6}\notin]-\pi ;\pi]\end{cases}\)
Donc inutile de prendre des valeurs de \(k\) supérieures pour la première solution.
Pour \(k=-1\):
\(\begin{cases}x=-\frac{\pi}{6}+2 \times (-1) \times \pi\\x=\frac{7\pi}{6}+2 \times (-1) \times\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}-\frac{12\pi}{6}=- \frac{11\pi}{6}\notin]-\pi ;\pi]\\x=\frac{7\pi}{6}-\frac{12\pi}{6}=-\frac{5\pi}{6} \in]-\pi ;\pi]\end{cases}\)
Donc inutile de prendre des valeurs de \(k\) inférieures pour la première solution.
Pour \(k=-2\):
\(x=\frac{7\pi}{6}+2 \times (-2) \times\pi\)
\(x=\frac{7\pi}{6}-\frac{24\pi}{6}=- \frac{17\pi}{6}\notin]-\pi ;\pi]\)
Donc inutile de prendre des valeurs de \(k\) inférieures pour la deuxième solution.
Les solutions dans \(]-\pi ;\pi]\) sont \(-\frac{\pi}{6}\) et \(-\frac{5\pi}{6}\)
Question
b. \(cos(x)=\frac{-\sqrt{3}}{2}\)
Solution
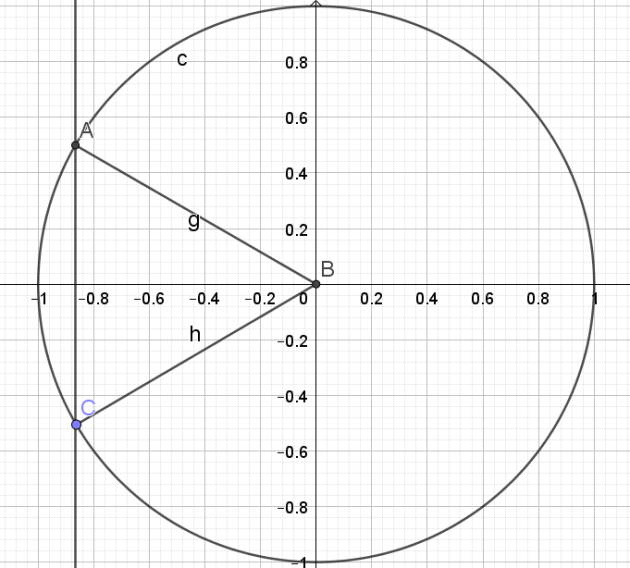
\(cos(x)=-\frac{\sqrt{3}}{2}=cos(-\frac{\pi}{6})\)
\(\iff \begin{cases}x=\pi-\frac{\pi}{6}+2k\pi\\x=-(\pi-\frac{\pi}{6})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{6\pi}{6}-\frac{\pi}{6}+2k\pi\\x=-(\frac{6\pi}{6}-\frac{\pi}{6})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{5\pi}{6}+2k\pi\\x=-\frac{5\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(\mathbb{R}\) sont :
\(\begin{cases}x=\frac{5\pi}{6}+2k\pi\\x=-\frac{5\pi}{6}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
RECHERCHE DES SOLUTIONS DANS \(]-\pi ;\pi]\) :
Pour \(k=0\) :
\(\begin{cases}x=-\frac{5\pi}{6}+2 \times 0 \times \pi\\x=\frac{5\pi}{6}+2 \times 0 \times\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{5\pi}{6} \in]-\pi ;\pi]\\x=\frac{-5\pi}{6} \in]-\pi ;\pi]\end{cases}\)
Pour \(k=1\) :
\(\begin{cases}x=-\frac{5\pi}{6}+2 \times 1 \times \pi\\x=\frac{5\pi}{6}+2 \times 1 \times\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{5\pi}{6}+\frac{12\pi}{6}=\frac{17\pi}{6} \notin]-\pi ;\pi]\\x=\frac{-5\pi}{6}+\frac{12\pi}{6}=\frac{7\pi}{6} \notin]-\pi ;\pi]\end{cases}\)
Donc inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\):
\(\begin{cases}x=-\frac{5\pi}{6}+2 \times (-1) \times \pi\\x=\frac{5\pi}{6}+2 \times (-1) \times\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{5\pi}{6}-\frac{12\pi}{6}=\frac{-7\pi}{6} \notin]-\pi ;\pi]\\x=\frac{-5\pi}{6}+\frac{-12\pi}{6}=\frac{-17\pi}{6} \notin]-\pi ;\pi]\end{cases}\)
Donc inutile de prendre des valeurs de \(k\) inférieures.
Les solutions dans ]-\pi ;\pi] sont \(\frac{5\pi}{6}\) et \(-\frac{5\pi}{6}\)
Question
b. \(cos(x)=0\)
Solution
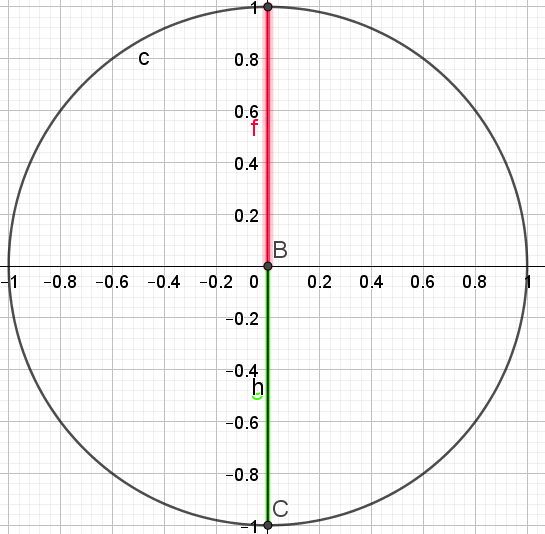
\(cos(x)=0=cos(\frac{\pi}{2})\)
\(\iff \begin{cases}x=\frac{\pi}{2}+2k\pi\\x=-\frac{\pi}{2}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(\mathbb{R}\) sont :
\(\begin{cases}x=\frac{\pi}{2}+2k\pi\\x=-\frac{\pi}{2}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
RECHERCHE DES SOLUTIONS DANS \(]-\pi ;\pi]\) :
Pour \(k=0\) :
\(\begin{cases}x=\frac{\pi}{2}+2 \times 0 \times \pi\\x=-\frac{\pi}{2}+2 \times 0 \times \pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\begin{cases}x=\frac{\pi}{2} \in]-\pi ;\pi]\\x=-\frac{\pi}{2}\in]-\pi ;\pi]\end{cases}\) \(k\in\mathbb{Z}\)
Pour \(k=1\) :
\(\begin{cases}x=\frac{\pi}{2}+2 \times 1 \times \pi\\x=-\frac{\pi}{2}+2 \times 1 \times \pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{2}+\frac{4\pi}{2}=\frac{5\pi}{2} \notin]-\pi ;\pi]\\x=-\frac{\pi}{2}+\frac{4\pi}{2}=\frac{3\pi}{2}\notin]-\pi ;\pi]\end{cases}\) \(k\in\mathbb{Z}\)
Donc inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\):
\(\begin{cases}x=\frac{\pi}{2}+2 \times (-1) \times \pi\\x=-\frac{\pi}{2}+2 \times (-1) \times \pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{2}-\frac{4\pi}{2}=\frac{-3\pi}{2} \notin]-\pi ;\pi]\\x=-\frac{\pi}{2}-\frac{4\pi}{2}=\frac{-5\pi}{2}\notin]-\pi ;\pi]\end{cases}\) \(k\in\mathbb{Z}\)
Donc inutile de prendre des valeurs de \(k\) inférieures.
Les solutions dans ]-\pi ;\pi] sont \(\frac{\pi}{2}\) et \(-\frac{\pi}{2}\)
Exercice 11
On se propose de résoudre dans l'intervalle \([0 ;2\pi[\),
l'équation (E) :
\((2sin x+\sqrt{3})(cos x-1)=0\)
Question
a. Se ramener à la résolution de deux équations, l'une en sin et l'autre en cos
Indice
\(\color{red}{\text{Propriété :Un produit de facteurs est nul }}\)
\(\color{red}{\text{si et seulement si}}\)
\(\color{red}{\text{un des facteurs au moins est nul.}}\)
Solution
\((2sin x+\sqrt{3})(cos x-1)=0\)
\(\color{red}{\text{Propriété :Un produit de facteurs est nul }}\)
\(\color{red}{\text{si et seulement si}}\)
\(\color{red}{\text{un des facteurs au moins est nul.}}\)
\(\iff 2sin x+\sqrt{3}=0 \)ou \(cos x-1=0\)
Question
b.Donner les solutions dans \(\mathbb{R}\), puis dans \(]-\pi ;\pi]\) de l'équation (E)
Solution
\(2sin x+\sqrt{3}=0 \)ou \(cos x-1=0\)
\(\iff 2sin x=-\sqrt{3} \)ou \(cos x=1\)
\(\iff sin x=\frac{-\sqrt{3}}{2} \)ou \(cos x=1\)
\(sin x=\frac{-\sqrt{3}}{2}\)
\(\iff sin x=sin(-\frac{\pi}{3})\)
\(\iff \begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\pi-(-\frac{\pi}{3})+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\frac{3\pi}{3}-(-\frac{\pi}{3})+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\frac{3\pi}{3}+\frac{\pi}{3}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
Les solutions dans \(\mathbb{R}\) sont donc :
\(\begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
RECHERCHE DES SOLUTIONS DANS \(]-\pi ;\pi]\) :
Pour \(k=0\) :
\(\begin{cases}x=-\frac{\pi}{3}+2 \times 0 \times \pi\\x=\frac{4\pi}{3}+2 \times 0 \times\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{3} \in]-\pi ;\pi]\\x=\frac{4\pi}{3} \notin]-\pi ;\pi]\end{cases}\)
Inutile de prendre des valeurs de \(k\) plus grandes pour la deuxième solution.
Pour \(k=1\) :
\(x=-\frac{\pi}{3}+2 \times 1 \times \pi\)
\(\iff x=-\frac{\pi}{3}+\frac{6\pi}{3}\)
\(\iff x=\frac{5\pi}{3} \notin]-\pi ;\pi]\)
Donc inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\):
\(\begin{cases}x=-\frac{\pi}{3}+2 \times (-1) \times \pi\\x=\frac{4\pi}{3}+2 \times (-1) \times\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{3}-\frac{6\pi}{3}=-\frac{7\pi}{3} \notin]-\pi ;\pi]\\x=\frac{4\pi}{3}-\frac{6\pi}{3}=-\frac{2\pi}{3} \in]-\pi ;\pi]\end{cases}\)
Inutile de prendre des valeurs de \(k\) plus petites pour la première solution.
Pour \(k=-2\):
\(x=\frac{4\pi}{3}+2 \times (-2) \times\pi\)
\(\iff x=\frac{4\pi}{3}-\frac{12\pi}{3}=-\frac{11\pi}{3} \notin]-\pi ;\pi]\)
Inutile de prendre des valeurs de \(k\) plus petites.
\(cos x=1\)
\(\iff cos x=cos 0\)
Les solutions dans \(\mathbb{R}\) sont donc :
\(x=0 +2 k\pi=2 k\pi\) \(k \in \mathbb{Z}\)
RECHERCHE DES SOLUTIONS DANS \(]-\pi ;\pi]\) :
Pour \(k=0\) :
\(x=0\)
Pour \(k=1\) :
\(x=2 \times 1 \times \pi=2 \pi \notin ]-\pi ;\pi]\)
Donc inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\):
\(x=2 \times (-1) \times \pi=-2 \pi \notin ]-\pi ;\pi]\)
Donc inutile de prendre des valeurs de \(k\) inférieures.
Les solutions dans \(\mathbb{R}\) sont donc :
\(\begin{cases}x=-\frac{\pi}{3}+2k\pi\\x=\frac{4\pi}{3}+2k\pi\\x=2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
Les solutions dans \(]-\pi ;\pi]\) sont donc :
\(\begin{cases}x=-\frac{\pi}{3} \\x=-\frac{2\pi}{3}\\x=0\end{cases}\)