Exercice : DS 2022
Exercice 2
Sachant que \(\cos(\frac{2\pi}{5})=\frac{\sqrt{5}-1}{4}\).
Question
1. Déterminer la valeur exacte de \(sin \frac{2\pi}{5}\) et \(sin \frac{3\pi}{5}.\)
Solution
\(\cos^2(x)+\sin^2(x)=1\) pour tout \(x\in \mathbb{R}\)
\(\cos^2(\frac{2\pi}{5})+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left ( \frac{\sqrt{5}-1}{4} \right )^2+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{\sqrt{5}^2-2\times \sqrt{5} \times 1+ 1^2}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left (\frac{5-2\sqrt{5}+1}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \left (\frac{6-2\sqrt{5}}{16} \right )+\sin^2(\frac{2\pi}{5})=1\)
\(\iff \sin^2(\frac{2\pi}{5})=1-\left (\frac{6-2\sqrt{5}}{16} \right )\)
\(\iff \sin^2(\frac{2\pi}{5})=\frac{16}{16}-\left (\frac{6-2\sqrt{5}}{16} \right )\)
\(\iff \sin^2(\frac{2\pi}{5})=\frac{10+2\sqrt{5}}{16}\)
\(\iff \sin(\frac{2\pi}{5})=\frac{\sqrt{10+2\sqrt{5}}}{4}\) ou \(\sin(\frac{2\pi}{5})=-\frac{\sqrt{10+2\sqrt{5}}}{4}\)
or \(\frac{2\pi}{5}=\frac{4\pi}{10} \in [0 ;\frac{\pi}{2}]=[0 ;\frac{5\pi}{10}]\)
donc \(\sin(\frac{2\pi}{5})=\frac{\sqrt{10+2\sqrt{5}}}{4}\)
\(sin (\pi-x)=sin(x)\) pour tout \(x \in \mathbb{R}\)
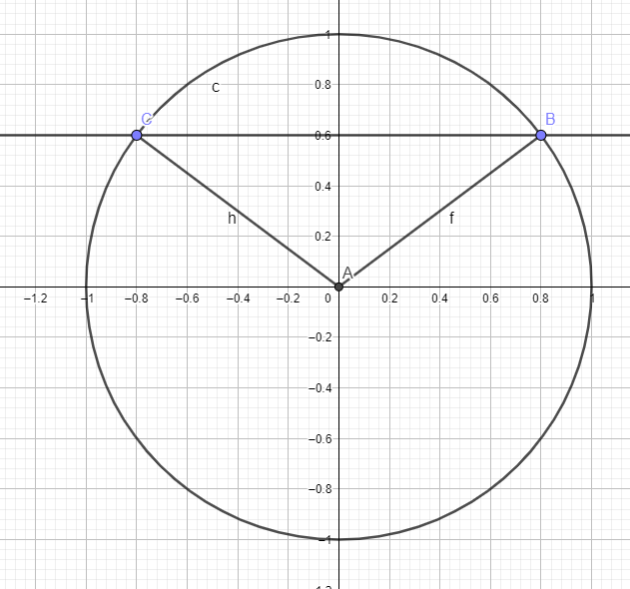
donc
\(sin (\pi-\frac{2\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{5\pi}{5}-\frac{2\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{3\pi}{5})= sin \frac{2\pi}{5}\)
\(\iff sin (\frac{3\pi}{5})= \frac{\sqrt{10+2\sqrt{5}}}{4}\)
Question
2.A l'aide du cercle trigonométrique, en déduire les valeurs de
\(cos(\frac{3\pi}{5})\) et \(sin(\frac{\pi}{10})\)
Solution
\(cos (\pi-x)=-cos(x)\) pour tout \(x \in \mathbb{R}\)
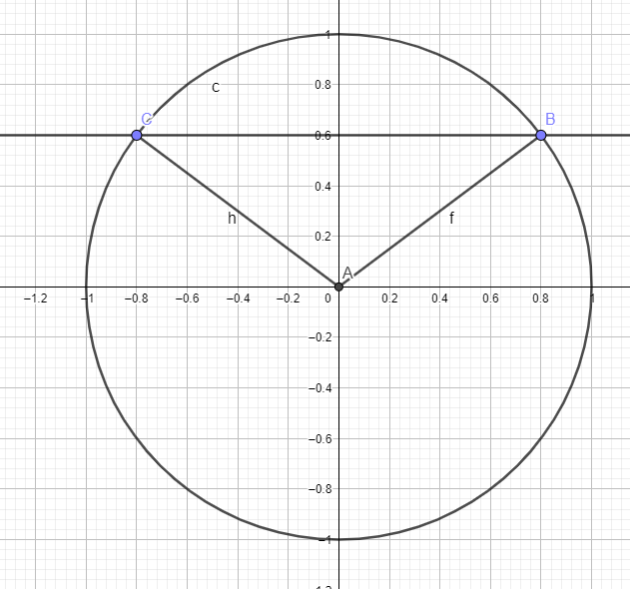
donc
\(\cos (\pi-\frac{2\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{5\pi}{5}-\frac{2\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{3\pi}{5})= -\cos \frac{2\pi}{5}\)
\(\iff \cos (\frac{3\pi}{5})= -\frac{\sqrt{5}-1}{4}\)
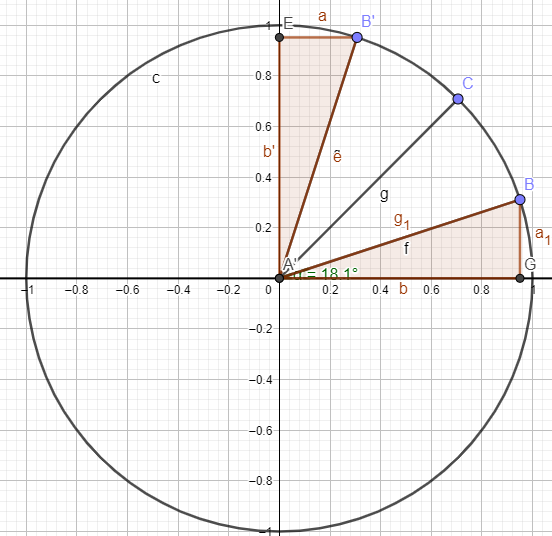
\(\sin(\frac{\pi}{2}-x)=\cos(x)\)
donc \(\sin(\frac{\pi}{2}-\frac{2\pi}{5})=\cos(\frac{2\pi}{5})\)
\(\iff \sin(\frac{5\pi}{10}-\frac{4\pi}{10})=\frac{\sqrt{5}-1}{4}\)
\(\iff \sin(\frac{\pi}{10})=\frac{\sqrt{5}-1}{4}\)
Exercice 3
Résoudre l'équation trigonométrique \(\cos x=\frac{\sqrt{3}}{2}\)
Question
dans \(\mathbb{R}\)
Solution
\(\cos x=\frac{\sqrt{3}}{2}\)
\(\iff x=\frac{\pi}{6}+2k\pi\) ou \(x=\frac{-\pi}{6}+2k\pi\) \(k \in \mathbb{Z}\)
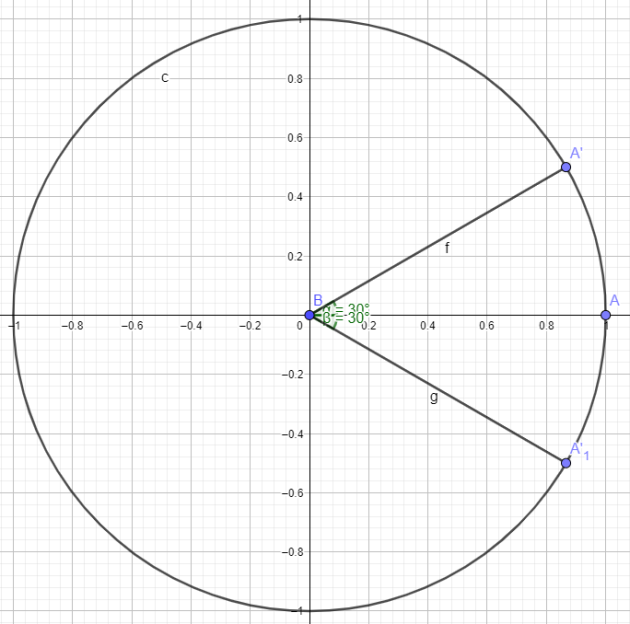
Question
pour \(x∈[−π;3π] .\)
Solution
Pour \(k=0\)
\(x=\frac{\pi}{6} \in [-\pi ;3\pi]\) ou \(x=\frac{-\pi}{6}\in [-\pi ;3\pi]\)
Pour \(k=1\)
\(x=\frac{\pi}{6}+2\pi=\frac{\pi}{6}+\frac{12\pi}{6}=\frac{13\pi}{6}\in [-\pi ;3\pi]\) ou
\(x=\frac{-\pi}{6}+2\pi=\frac{-\pi}{6}+\frac{12\pi}{6}=\frac{11\pi}{6}\in [-\pi ;3\pi]\)
Pour \(k=2\)
\(x=\frac{\pi}{6}+4\pi=\frac{\pi}{6}+\frac{24\pi}{6}=\frac{25\pi}{6}\notin [-\pi ;3\pi]=[-\frac{6\pi}{6} ;\frac{18\pi}{6}]\)
ou
\(x=\frac{-\pi}{6}+4\pi=\frac{-\pi}{6}+\frac{24\pi}{6}=\frac{23\pi}{6} \notin [-\pi ;3\pi]=[-\frac{6\pi}{6} ;\frac{18\pi}{6}]\)
Ces deux valeurs n'appartiennent pas à \([-\pi ;3\pi]\) et sont trop grandes.
Inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\)
\(x=\frac{\pi}{6}-2\pi=\frac{\pi}{6}-\frac{12\pi}{6}=-\frac{11\pi}{6} \notin [-\pi ;3\pi]\)
ou
\(x=\frac{\pi}{6}-2\pi=\frac{\pi}{6}-\frac{12\pi}{6}=\frac{-11\pi}{6}\notin [-\pi ;3\pi]\)
Ces valeurs sont trop petites. Inutile de prendre des valeurs de \(k\) plus petites.
Les solutions dans \([-\pi ;3\pi]\) sont donc
\(S=\{\frac{-\pi}{6} ;\frac{\pi}{6} ;\frac{11\pi}{6} ;\frac{12\pi}{6}\} \)
Exercice 4
Soit :
la \(\color{magenta}{\text{Propriété 1 :}}\) "Si \(x\in]0 ;\pi[\), alors \(\sin(x)>0\)
la \(\color{magenta}{\text{Propriété 2 :}}\) "Si \(x\) est un réel strictement positif, alors \(\sin(x)>0\)
la \(\color{magenta}{\text{Propriété 3 :}}\) "Si \(x\in]0 ;\pi[\) alors \(\cos x>0\)
Question
1.Dire parmi les propriétés précédentes celles qui sont vraies.Justifier.
Solution
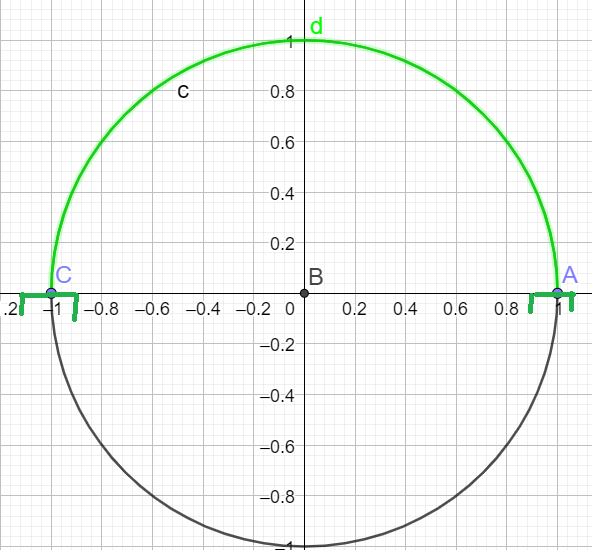
la \(\color{magenta}{\text{Propriété 1 :}}\) "Si \(x\in]0 ;\pi[\), alors \(\sin(x)>0\) est vraie
Pour les angles dont la mesure est représentée par un point de l'arc de cercle en vert, le sinus est strictement positif.
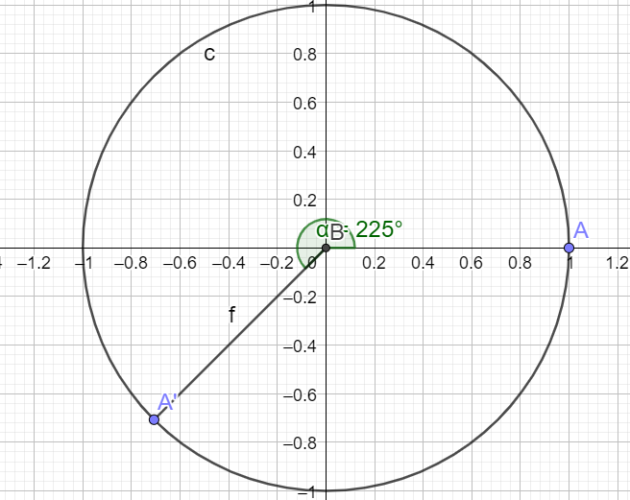
la \(\color{magenta}{\text{Propriété 2 :}}\) "Si \(x\) est un réel strictement positif, alors \(\sin(x)>0\) est fausse.
Contre-exemple :
\(sin(\frac{5\pi}{4})=\frac{-\sqrt{2}}{2}\)
car \(\frac{5\pi}{4}>0\) et \(sin(\frac{5\pi}{4})<0\)
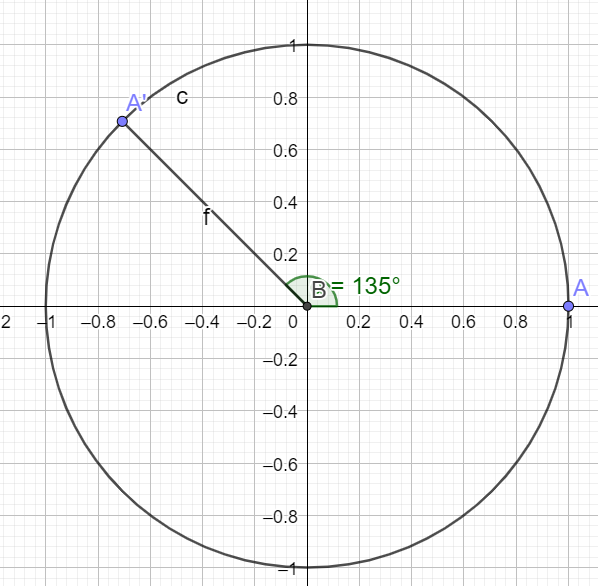
la \(\color{magenta}{\text{Propriété 3 :}}\) "Si \(x\in]0 ;\pi[\) alors \(\cos x>0\) est fausse.
Contre-exemple :
\(\cos(\frac{3\pi}{4})=\frac{-\sqrt{2}}{2}\)
\(\frac{3\pi}{4} \in ]0 ;\pi[\) et \(\cos(\frac{3\pi}{4}<0\)
Question
2.Ecrire les propriétés réciproques.Dire si ces propriétés sont vraies ?
Solution
la \(\color{magenta}{\text{Réciproque de la Propriété 1 :}}\) "Si \(\sin(x)>0\), alors \(x\in]0 ;\pi[\) est fausse.
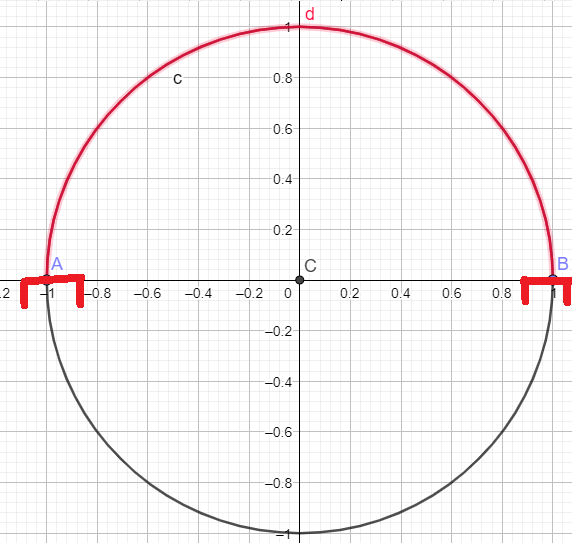
la \(\color{magenta}{\text{Propriété Réciproque Correcte 1 :}}\) "Si \(\sin(x)>0\) alors \(x\in]0+2k\pi ;\pi+2k\pi[\) \(k\in \mathbb{Z}\)
la \(\color{magenta}{\text{Réciproque de la Propriété 2 :}}\) "Si \(\sin(x)>0\), alors \(x\) est un réel strictement positif est fausse.

la \(\color{magenta}{\text{Propriété Réciproque Correcte 2 :}}\) "Si \(\sin(x)>0\) alors \(x\in]0+2k\pi ;\pi+2k\pi[\) \(k\in \mathbb{Z}\)
la \(\color{magenta}{\text{Réciproque de la Propriété 3 :}}\) "Si \(\cos x>0\) alors \(x\in]0 ;\pi[\)
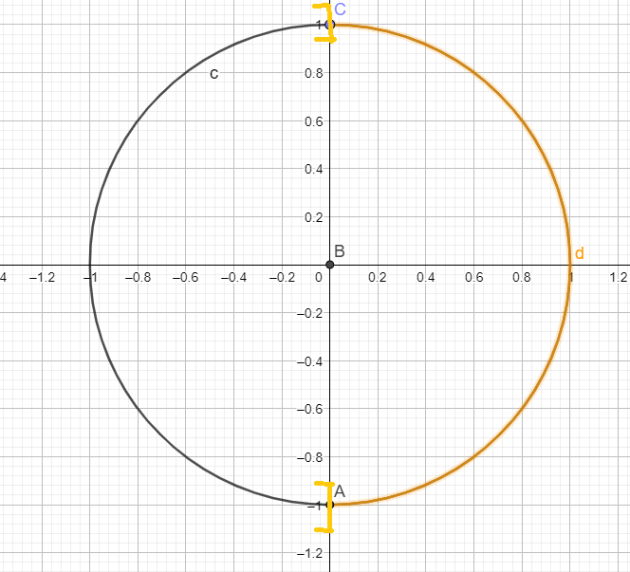
la \(\color{magenta}{\text{Propriété Réciproque Correcte 3 :}}\) "Si \(\cos(x)>0 \)alors \(x\in ]-\frac{\pi}{2}+2k\pi ;\frac{\pi}{2}+2k\pi[\) \(k \in \mathbb{Z}\)
Exercice 5
.
Question
1. Calculer la valeur exacte des nombres réels A ,B et C
\(A=cos(\frac{\pi}{6})+cos(\frac{\pi}{3})\)
\(B=sin(\frac{\pi}{6})+sin(\frac{\pi}{3})\)
Solution
\(A=cos(\frac{\pi}{6})+cos(\frac{\pi}{3})\)
\(\iff A=\frac{\sqrt{3}}{2}+\frac{1}{2}\)
\(\iff A=\frac{1+\sqrt{3}}{2}\)
\(B=sin(\frac{\pi}{6})+sin(\frac{\pi}{3})\)
\(\iff B=\frac{1+\sqrt{3}}{2}\)
Question
2.Comment peut on expliquer cette propriété ?
Solution
On a la relation :
\(\sin(\frac{\pi}{2}-x)=\cos(x)\)
donc
\(\sin(\frac{\pi}{2}-\frac{\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{3\pi}{6}-\frac{\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{2\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{\pi}{3})=\cos(\frac{\pi}{6})\)
\(\sin(\frac{\pi}{2}-\frac{\pi}{3})=\cos(\frac{\pi}{3})\)
\(\iff \sin(\frac{3\pi}{6}-\frac{2\pi}{6})=\cos(\frac{\pi}{3})\)
\(\iff \sin(\frac{\pi}{6})=\cos(\frac{\pi}{3})\)
Question
3. Calculer
\(C=cos 0 + cos \frac{\pi}{3}+ cos \frac{2\pi}{3}+ cos \pi + cos \frac{4\pi}{3}+ cos\frac{5\pi}{3}\)
Solution
\(C=cos 0 + cos \frac{\pi}{3}+ cos \frac{2\pi}{3}+ cos \pi + cos \frac{4\pi}{3}+ cos\frac{5\pi}{3}\)
\(\iff C=1 + \frac{1}{2}-\frac{1}{2} -1 -\frac{1}{2}+\frac{1}{2}\)
\(\iff C=0\)
Exercice 6
.
Question
Montrer que pour tout réel \(x\) :
\((2cos x+3sin x)^2+(3cos x-2sin x)^2=13\)
Solution
\((2cos x+3sin x)^2+(3cos x-2sin x)^2\)
\(=(2\cos x)^2+2\times 2 \cos x \times 3 \sin x+(3\sin x)^2+(3\cos x)^2-2 \times 3\cos x \times 2\sin x+(2\sin x)^2\)
\(=4\cos^2 x+12\cos x \times \sin x+9\sin^2 x+9\cos^2 x-12\cos x \times \sin x+4\sin^2 x\)
\(=13\cos^2 x+13\sin^2 x\)
\(=13(\cos^2 x+\sin^2 x)\)
\(=13 \times 1=13\)
car \(\cos^2 x+\sin^2 x=1\)