Exercice : DS 2022
Exercice 1
Quand cela est possible, les exercices peuvent être complété directement sur cet énoncé.
Sauf mention contraire, une explication, même courte, est attendue pour chaque question.
Exercice 1 :
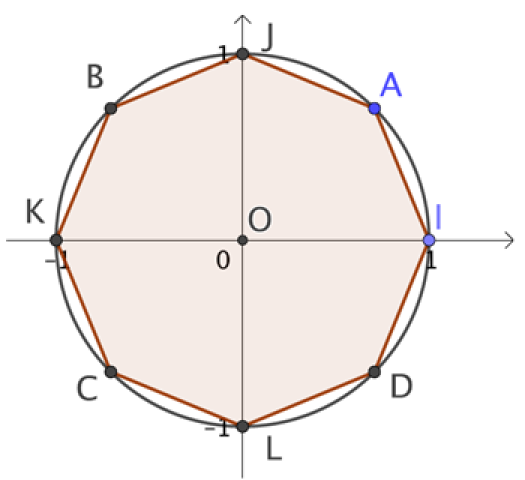
On a tracé l'octogone régulier IAJBKCLD dans le cercle trigonométrique :
Question
1. Compléter le tableau suivant sans justifier :
\(x\) | \(\frac{\pi}{4}\) | \(\pi\) | \(\frac{-17\pi}{2}\) | |||
|---|---|---|---|---|---|---|
Point-image | B | C | ||||
\(\cos(x)\) | \(\frac{\sqrt{2}}{2}\) | -1 | ||||
\(\sin(x)\) |
Solution
\(x\) | \(\frac{\pi}{4}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{4}=\frac{-3\pi}{4}+2\pi\) | \(\pi\) | \(\frac{-17\pi}{2}\) \(=\frac{-\pi}{2}\) | \(\pi=-\pi+2\pi\) |
|---|---|---|---|---|---|---|
Point-image | A | B | C | J | L | L |
\(\cos(x)\) | \(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | -1 | 0 | -1 |
\(\sin(x)\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | 0 | -1 | 0 |
Déterminons la mesure principale associée à la mesure \(\frac{-17\pi}{2}\):
\(\frac{\frac{-17\pi}{2}}{2\pi}\)=\(\frac{\frac{-17\pi}{2}}{\frac{2\pi}{1}}\)
\(=\frac{-17\pi}{2} \times \frac{1}{2\pi}\)
\(=\frac{-17}{4}=-4,25\)
\(\frac{-17\pi}{2} +4 \times 2\pi=\frac{-17\pi}{2} +8\pi\)
\(=\frac{-17\pi}{2} +\frac{16\pi}{2}=\frac{-\pi}{2}\)
La mesure principale associée à la mesure \(\frac{-17\pi}{2}\) est donc \(\frac{-\pi}{2}\)
Question
2. Compléter le tableau suivant sans justifier :
Angle | \(\widehat{IOA}\) | \(\widehat{AOK}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | |||
Mesure en ° |
Solution
Angle | \(\widehat{IOA}\) | \(\widehat{AOK}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | \(\frac{\pi}{4}\) | \(\pi-\frac{\pi}{4}=\frac{3\pi}{4}\) | \(\frac{3\pi}{8}\) |
Mesure en ° | 45 | 135 | 67,5 |
La somme des mesures des trois angles d'un triangle vaut 180° ou \(\pi\) radians.
\(\widehat{IOA}+\widehat{IAO}+\widehat{OIA}=\pi\)
Le triangle OAI est isocèle en O car OA=OI.
En effet [OA] et [OI] sont les rayons du cercle trigonométrique.
donc \(\widehat{IAO}=\widehat{OIA}\)
\(\iff \frac{\pi}{4}+2\widehat{IAO}=\pi\)
\(\iff 2\widehat{IAO}=\pi-\frac{\pi}{4}\)
\(\iff 2\widehat{IAO}=\frac{4\pi}{4}-\frac{\pi}{4}\)
\(\iff 2\widehat{IAO}=\frac{3\pi}{4}\)
\(\iff \widehat{IAO}=\frac{3\pi}{8}\)
Question
3. Quelle est la longueur de l'arc \(\overset{\huge{\frown}}{IA\:}\) ?
Celle de l'arc \(\overset{\huge{\frown}}{CD\:}\) ?
Solution
La longueur de l'arc \(\overset{\huge{\frown}}{IA\:}\)
représente \(\frac{1}{8}\) du périmètre du cercle trigonométrique donc :
\(\overset{\huge{\frown}}{IA\:}=\frac{1}{8} \times 2\pi=\frac{\pi}{4}\)
La longueur de l'arc \(\overset{\huge{\frown}}{CD\:}\)
représente \(\frac{2}{8}=\frac{1}{4}\) du périmètre du cercle trigonométrique donc :
\(\overset{\huge{\frown}}{IA\:}=\frac{1}{4} \times 2\pi=\frac{\pi}{2}\)
Question
4. Tracer dans le triangle OAI la hauteur [AH] issue de A puis en déterminer la longueur à l'aide du théorème de Pythagore.
Solution
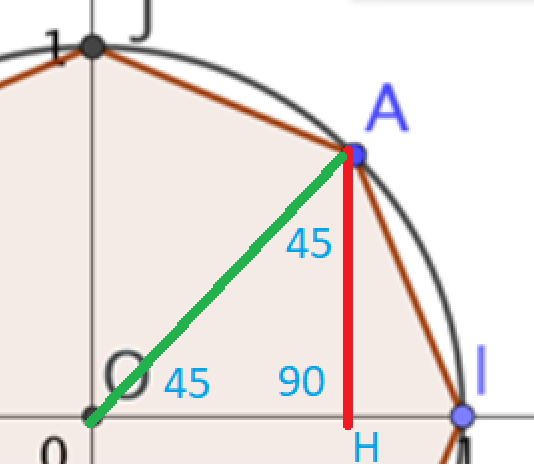
Le triangle OAH est isocèle en H
En effet, la somme des mesures des trois angles d'un triangle vaut 180° ou \(\pi\) radians.
\(\widehat{OHA}+\widehat{HAO}+\widehat{HOA}=\pi\)
\(\begin{cases} \widehat{OHA}=\frac{\pi}{2}\\\widehat{HOA}=\frac{\pi}{4}\end{cases}\)
\(\frac{\pi}{2}+\frac{\pi}{4}+\widehat{HOA}=\pi\)
\(\iff \frac{2\pi}{4}+\frac{\pi}{4}+\widehat{HOA}=\frac{4\pi}{4}\)
\(\iff \frac{3\pi}{4}+\widehat{HOA}=\frac{4\pi}{4}\)
\(\iff \widehat{HOA}=\frac{4\pi}{4}-\frac{3\pi}{4}=\frac{\pi}{4}\)
donc \(\widehat{HOA}=\widehat{HOA}=\frac{\pi}{4}\)
Le triangle OAH a donc deux angles de même mesure
donc HA=OH
Utilisons le théorème de Pythagore dans le triangle OHA rectangle en H
\(OA^2=OH^2+HA^2\)
\(\iff 1^2=HA^2+HA^2\)
\(\iff 1=2HA^2\)
\(\iff \frac{1}{2}=HA^2\)
\(\iff HA^2=\frac{1}{2}\)
\(\iff HA=\frac{1}{\sqrt{2}}\)
\(\iff HA=\frac{\sqrt{2}}{2}\)
Question
5. En déduire l'aire du triangle OAI puis celle de l'octogone IAJBKCLD.
Solution
Aire du triangle OAI :
\(Aire_{OAI}=\frac{base \times Hauteur}{2}\)
\(\iff Aire_{OAI}=\frac{OI \times AH}{2}\)
\(\iff Aire_{OAI}=\frac{OI \times AH}{2}\)
\(\iff Aire_{OAI}=\frac{1 \times \sqrt{2}{2}}{2}\)
\(\iff Aire_{OAI}=\frac{\frac{\sqrt{2}}{2}}{2}\)
\(\iff Aire_{OAI}=\frac{\sqrt{2}{2}}{\frac{1}{2}}\)
\(\iff Aire_{OAI}=\sqrt{2}{2} \times \frac{1}{2}\)
\(\iff Aire_{OAI}=\sqrt{2}{4}\)
L'aire de l'octogone est composé de 8 triangles isométriques au triangle OAI :
\(Aire_{Octogone}=\sqrt{2}{4} \times 8=2\sqrt{2}\)
Exercice 2
Sachant que \(\cos(\frac{\pi}{12})=\frac{\sqrt{2}+\sqrt{6}}{4}\).
Question
1. Déterminer la valeur exacte de \(sin \frac{\pi}{12}\) et \(sin \frac{11\pi}{12}.\)
Solution
\(\cos^2(x)+\sin^2(x)=1\) pour tout \(x\in \mathbb{R}\)
\(\cos^2(\frac{\pi}{12})+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{\sqrt{2}+\sqrt{6}}{4} \right )^2+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{\sqrt{2}^2+2\times \sqrt{2} \times \sqrt{6}+ \sqrt{6}^2}{16} \right )+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{2+2\sqrt{12}+6}{16} \right )+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{8+2\sqrt{12}}{16} \right )+\sin^2(\frac{\pi}{12})=1\)
\(\iff \left (\frac{8+2\sqrt{12}}{16} \right )+\sin^2(\frac{\pi}{12})=1\)
\(\iff \sin^2(\frac{\pi}{12})=1-\left (\frac{8+2\sqrt{12}}{16} \right )\)
\(\iff \sin^2(\frac{\pi}{12})=\frac{16}{16}-\left (\frac{8+2\sqrt{12}}{16} \right )\)
\(\iff \sin^2(\frac{\pi}{12})=\frac{8-2\sqrt{12}}{16}\)
\(\iff \sin(\frac{\pi}{12})=\frac{\sqrt{8-2\sqrt{12}}}{4}\) ou \(\sin(\frac{\pi}{12})=-\frac{\sqrt{8-2\sqrt{12}}}{4}\)
or \(\frac{\pi}{12}\in [0 ;\frac{\pi}{2}]\)
donc \(\sin(\frac{\pi}{12})=\frac{\sqrt{8-2\sqrt{12}}}{4}\)
On a montré que
\((\sqrt{2}+\sqrt{6})^2=8+2\sqrt{12}\)
donc de manière identique, on peut penser que \(8-2\sqrt{12}=(\sqrt{2}-\sqrt{6})^2\),
démontrons le :
\((\sqrt{2}-\sqrt{6})^2=\sqrt{2}^2-2\times \sqrt{2} \times \sqrt{6}+ \sqrt{6}^2\)
\(\iff (\sqrt{2}-\sqrt{6})^2=2-2\sqrt{12}+ 6\)
\(\iff (\sqrt{2}-\sqrt{6})^2=8-2\sqrt{12}\)
donc \(\sin(\frac{\pi}{12})=\frac{\sqrt{(\sqrt{2}-\sqrt{6})^2}}{4}\)
donc \(\sin(\frac{\pi}{12})=\frac{\sqrt{6}-\sqrt{2}}{4}\)
\(\sin \frac{11\pi}{12}=\sin \frac{\pi}{12}==\frac{\sqrt{6}-\sqrt{2}}{4}\)
car \(\sin (\pi-x)=\sin x\)
Question
2.A l'aide du cercle trigonométrique, en déduire les valeurs de
\(cos(\frac{11\pi}{12})\) et \(sin(\frac{5\pi}{12})\)
Exercice 3
Résoudre l'équation trigonométrique \(\sin x=\frac{\sqrt{3}}{2}\)
Question
dans \(\mathbb{R}\),
Solution
\(\sin x=\frac{\sqrt{3}}{2}\)
\(\iff x=\frac{\pi}{3}+2k\pi\) ou \(x=\frac{2\pi}{3}+2k\pi\) \(k \in \mathbb{Z}\)
Question
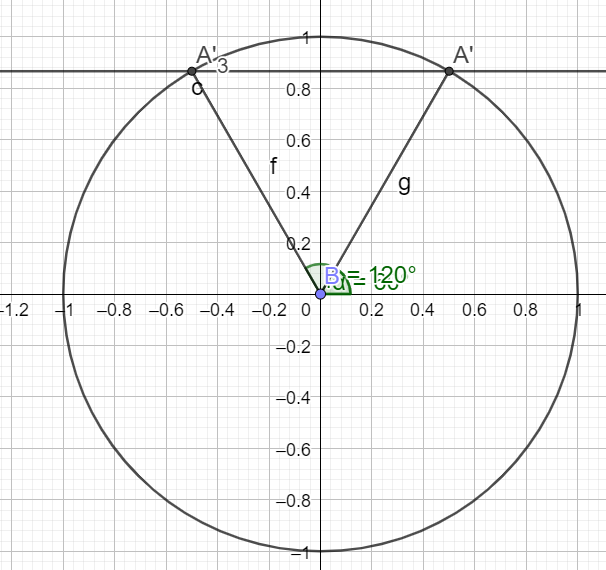
pour \(x∈[−π;3π] .\)
Solution
Pour \(k=0\)
\(x=\frac{\pi}{3}\in [-\pi ;3\pi]=[-\frac{3\pi}{3} ;\frac{9\pi}{3}] \)ou \(x=\frac{2\pi}{3} \in [-\pi ;3\pi]=[-\frac{3\pi}{3} ;\frac{9\pi}{3}]\)
Pour \(k=1\)
\(x=\frac{\pi}{3}+2\pi=\frac{\pi}{3}+\frac{6\pi}{3}=\frac{7\pi}{3}\in [-\pi ;3\pi]\)
ou
\(x=\frac{2\pi}{3}+2\pi=\frac{2\pi}{3}+\frac{6\pi}{3}=\frac{8\pi}{3}\in [-\pi ;3\pi]\)
Pour \(k=2\)
\(x=\frac{\pi}{3}+4\pi=\frac{\pi}{3}+\frac{12\pi}{3}=\frac{13\pi}{3}\in [-\pi ;3\pi]\)
ou
\(x=\frac{2\pi}{3}+4\pi=\frac{2\pi}{3}+\frac{12\pi}{3}=\frac{14\pi}{3} \notin [-\pi ;3\pi]\)
Ces deux valeurs n'appartiennent pas à \([-\pi ;3\pi]\) et sont trop grandes.
Inutile de prendre des valeurs de \(k\) supérieures.
Pour \(k=-1\)
\(x=\frac{\pi}{3}-2\pi=\frac{\pi}{3}-\frac{6\pi}{3}=-\frac{5\pi}{3} \notin [-\pi ;3\pi]\)
ou
\(x=\frac{2\pi}{3}-2\pi=\frac{2\pi}{3}-\frac{6\pi}{3}=\frac{-4\pi}{3}\notin [-\pi ;3\pi]\)
Ces valeurs sont trop petites. Inutile de prendre des valeurs de \(k\) plus petites.
Les solutions dans \([-\pi ;3\pi]\) sont donc
\(S=\{\frac{\pi}{3} ;\frac{\pi}{3} ;\frac{7\pi}{3} ;\frac{8\pi}{3}\} \)
Exercice 4
Soit :
la \(\color{magenta}{\text{Propriété 1 :}}\) "Si \(x\in]0 ;\frac{\pi}{2}[\), alors \(\sin(x)>0\)
la \(\color{magenta}{\text{Propriété 2 :}}\) "Si \(x\) est un réel strictement négatif, alors \(\sin(x)<0\)
la \(\color{magenta}{\text{Propriété 3 :}}\) "Si \(x\in]0 ;\frac{\pi}{2}[\) alors \(\cos x>0\)
Question
1.Dire parmi les propriétés précédentes celles qui sont vraies.Justifier.
Solution
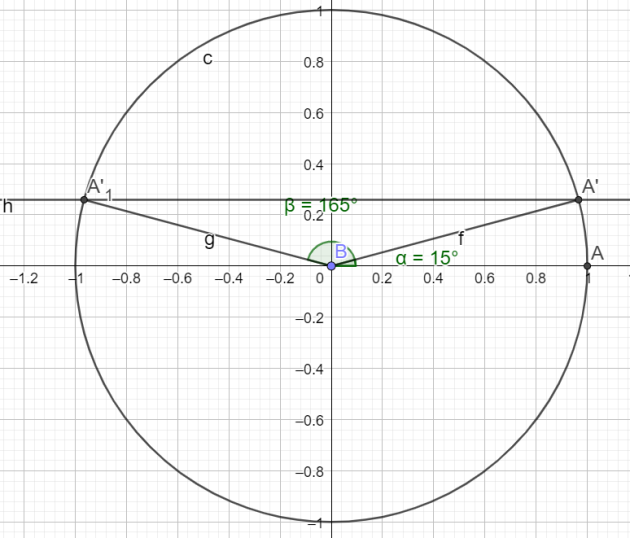
la \(\color{magenta}{\text{Propriété 1 :}}\) "Si \(x\in]0 ;\frac{\pi}{2}[\), alors \(\sin(x)>0\) est vraie.
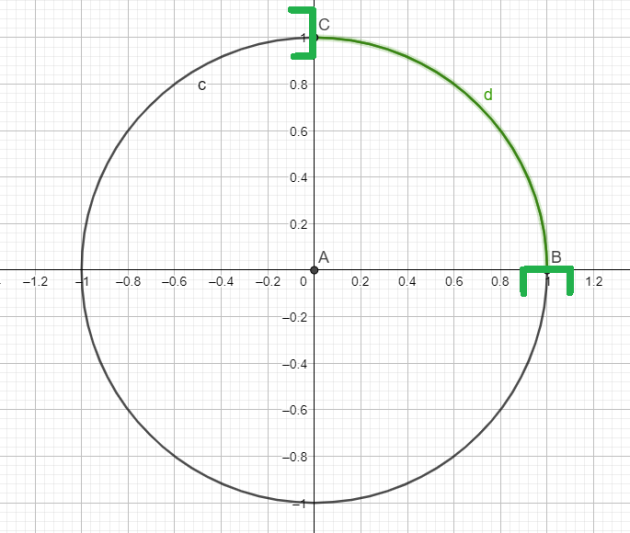
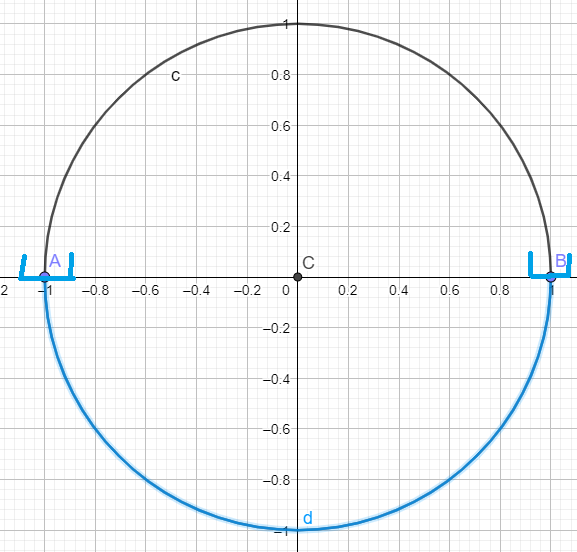
Pour les angles dont la mesure est représentée par un point de l'arc de cercle en vert, le sinus est strictement positif.
Cet arc de cercle rouge correspond dans l'intervalle des mesures principales aux mesures \(]0 ;\frac{\pi}{2}[\)
la \(\color{magenta}{\text{Propriété 2 :}}\) "Si \(x\) est un réel strictement négatif, alors \(\sin(x)<0\) est fausse.
Contre-exemple :
\(sin(\frac{-3\pi}{4})=\frac{\sqrt{2}}{2}\)
or \(\frac{-3\pi}{4}<0\) et \(sin(\frac{-3\pi}{4})>0\)
la \(\color{magenta}{\text{Propriété 3 :}}\) "Si \(x\in]0 ;\frac{\pi}{2}[\) alors \(\cos x>0\) est vraie.

Pour les angles dont la mesure est représentée par un point de l'arc de cercle en vert, le cosinus est strictement positif.
Cet arc de cercle vert correspond dans l'intervalle des mesures principales aux mesures \(]0 ;\frac{\pi}{2}[\)
Question
2.Ecrire les propriétés réciproques.Dire si ces propriétés sont vraies ?
Solution
la \(\color{magenta}{\text{Propriété Réciproque 1 :}}\) "Si \(\sin(x)>0\) alors \(x\in]0 ;\frac{\pi}{2}[\) est fausse.
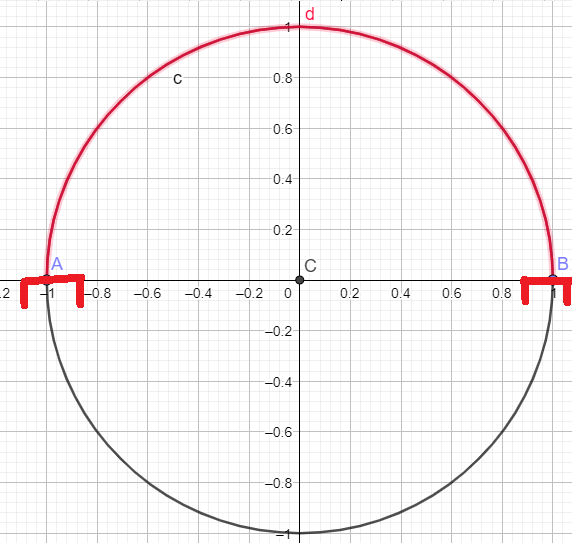
la \(\color{magenta}{\text{Propriété Réciproque Correcte 1 :}}\) "Si \(\sin(x)>0\) alors \(x\in]0+2k\pi ;\pi+2k\pi[\) \(k\in \mathbb{Z}\)
la \(\color{magenta}{\text{Propriété Réciproque 2 :}}\) "Si \(\sin(x)<0 \)\(alors x\) est un réel strictement négatif est fausse.
la \(\color{magenta}{\text{Propriété Réciproque Correcte 2 :}}\) "Si \(\sin(x)<0 \)alors \(x\in ]-\pi+2k\pi ;0+2k\pi[\) \(k \in \mathbb{Z}\)
la \(\color{magenta}{\text{Propriété Réciproque 3 :}}\) "Si \(\cos x>0\) alors \(x\in]0 ;\frac{\pi}{2}[\) est fausse.
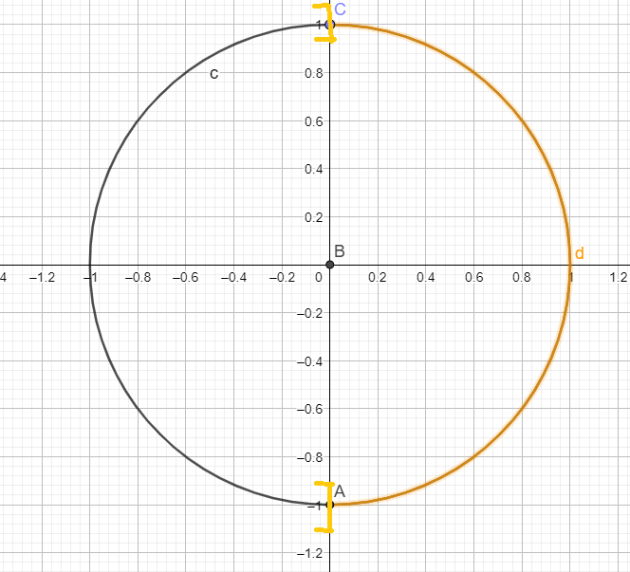
la \(\color{magenta}{\text{Propriété Réciproque Correcte 3 :}}\) "Si \(\cos(x)>0 \)alors \(x\in ]-\frac{\pi}{2}+2k\pi ;\frac{\pi}{2}+2k\pi[\) \(k \in \mathbb{Z}\)
Exercice 5
.
Question
1. Calculer la valeur exacte des nombres réels A ,B et C
\(A=cos(0)+cos(\frac{\pi}{6})+cos(\frac{\pi}{4})+cos(\frac{\pi}{3})+cos(\frac{\pi}{2})\)
\(B=sin(0)+sin(\frac{\pi}{6})+sin(\frac{\pi}{4})+sin(\frac{\pi}{3})+sin(\frac{\pi}{2})\)
Solution
\(A=cos(0)+cos(\frac{\pi}{6})+cos(\frac{\pi}{4})+cos(\frac{\pi}{3})+cos(\frac{\pi}{2})\)
\(\iff A=1+\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}+\frac{1}{2}+0\)
\(\iff A=1+\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}+\frac{1}{2}+0\)
\(\iff A=\frac{3+\sqrt{3}+\sqrt{2}}{2}\)
\(B=sin(0)+sin(\frac{\pi}{6})+sin(\frac{\pi}{4})+sin(\frac{\pi}{3})+sin(\frac{\pi}{2})\)
\(\iff B=0+\frac{1}{2}+\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}+1\)
\(\iff B=\frac{3+\sqrt{2}}{2}+\frac{\sqrt{3}}{2}+1\)
\(\iff B=\frac{3+\sqrt{2}+\sqrt{3}}{2}\)
Question
2.Comment peut on expliquer cette propriété ?
Solution
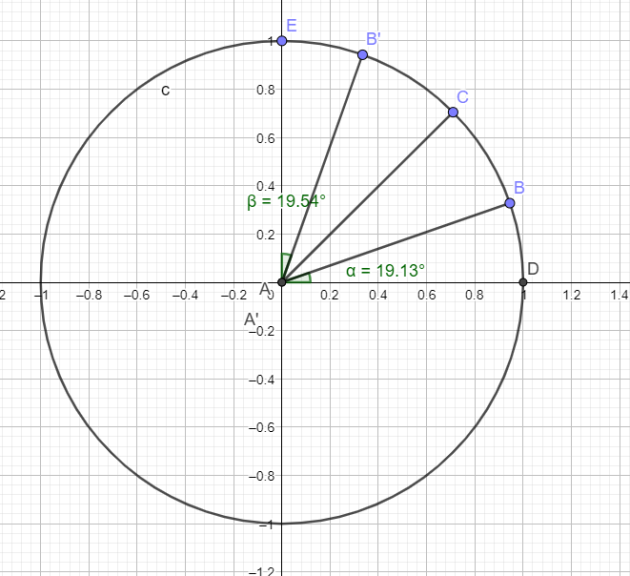
On a la relation :
\(\sin(\frac{\pi}{2}-x)=\cos(x)\)
donc
\(\sin(\frac{\pi}{2}-\frac{\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{3\pi}{6}-\frac{\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{2\pi}{6})=\cos(\frac{\pi}{6})\)
\(\iff \sin(\frac{\pi}{3})=\cos(\frac{\pi}{6})\)
\(\sin(\frac{\pi}{2}-\frac{\pi}{3})=\cos(\frac{\pi}{3})\)
\(\iff \sin(\frac{3\pi}{6}-\frac{2\pi}{6})=\cos(\frac{\pi}{3})\)
\(\iff \sin(\frac{\pi}{6})=\cos(\frac{\pi}{3})\)
\(\sin(\frac{\pi}{2}-0)=\cos(0)\)
\(\iff \sin(\frac{\pi}{2})=\cos(0)\)
\(\sin(\frac{\pi}{2}-\frac{\pi}{4})=\cos(\frac{\pi}{4})\)
\(\iff \sin(\frac{2\pi}{4}-\frac{\pi}{4})=\cos(\frac{\pi}{4})\)
\(\iff \sin(\frac{\pi}{4})=\cos(\frac{\pi}{4})\)
Question
3. Calculer
\(C=sin 0 + sin \frac{\pi}{3}+ sin \frac{2\pi}{3}+ sin \pi + sin \frac{4\pi}{3}+ sin\frac{5\pi}{3}\)
Solution
\(C=sin 0 + sin \frac{\pi}{3}+ sin \frac{2\pi}{3}+ sin \pi + sin \frac{4\pi}{3}+ sin\frac{5\pi}{3}\)
\(\iff C=0 + \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}+0-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\)
\(\iff C=0 + \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}+0-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\)
\(\iff C=0\)
Exercice 6
.
Question
Montrer que pour tout réel \(x\) :
\((cos x+sin x)^2+(cos x-sin x)^2=2\)
Solution
\((cos x+sin x)^2+(cos x-sin x)^2\)
\(=\cos^2 x+2\cos x \times \sin x+\sin^2 x+\cos^2 x-2\cos x \times \sin x+\sin^2 x\)
\(=2\cos^2 x+2\sin^2 x\)
\(=2(\cos^2 x+\sin^2 x)\)
\(=2 \times 1=2\)
car \(\cos^2 x+\sin^2 x=1\)